Hình chóp tam giác đều là một thể hình học nổi bật trong không gian ba chiều. Các công thức tính diện tích và thể tích của hình chóp này rất quan trọng khi giải quyết các bài toán thuộc lĩnh vực hình học không gian. Để nắm vững hơn về các đặc điểm, tính chất cũng như phương pháp tính toán, bạn hãy cùng tìm hiểu những nội dung chi tiết dưới đây.
Hình chóp tam giác đều là gì?
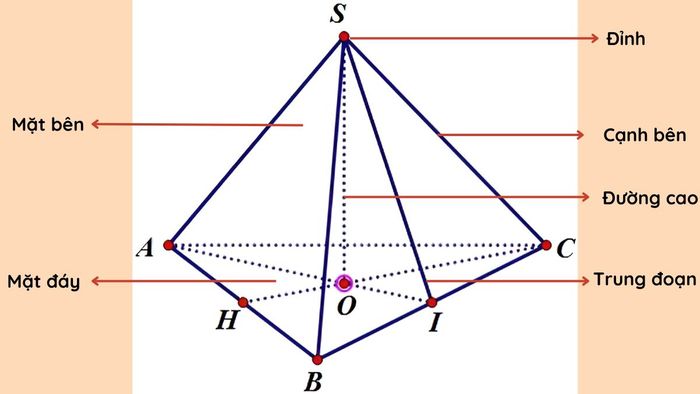
Hình chóp tam giác đều là một hình học không gian, có đáy là một tam giác đều, còn các mặt bên của nó đều là các tam giác vuông cân. Cấu trúc này tạo thành một đỉnh nhọn, nằm trên một mặt phẳng vuông góc với đáy. Các mặt bên của hình chóp đều có diện tích đồng nhất, tạo nên sự đối xứng hoàn hảo cho hình học này.
Đặc biệt, tam giác đáy của hình chóp tam giác đều có các cạnh có độ dài giống nhau, từ đó tạo ra sự đối xứng hoàn hảo cho các mặt bên và toàn bộ hình chóp. Đây là một loại hình chóp rất phổ biến trong các bài toán hình học không gian, đặc biệt là trong việc tính toán diện tích và thể tích.

Các tính chất của hình chóp tam giác đều
Hình chóp tam giác đều sở hữu tính đối xứng nổi bật, với ba mặt tam giác bên đều có dạng vuông cân đồng nhất. Diện tích xung quanh hình chóp này được tính bằng tổng diện tích của ba mặt bên, mỗi mặt là một tam giác vuông cân. Điều này giúp cho việc tính toán trở nên đơn giản và dễ dàng hơn.
Hình chóp tam giác đều còn có tính đối xứng qua một mặt phẳng đi qua đỉnh và các cạnh của đáy. Khi cắt hình chóp theo mặt phẳng này, bạn sẽ thu được hai nửa đối xứng hoàn hảo. Tính chất đối xứng này không chỉ làm tăng tính thẩm mỹ mà còn giúp ích trong việc tính toán diện tích và thể tích của hình chóp.
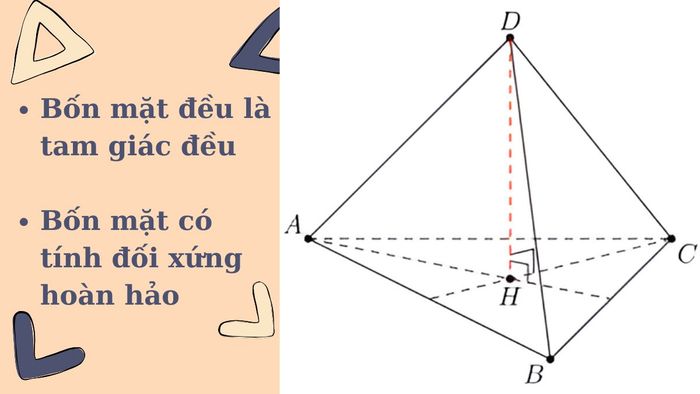
So sánh hình chóp tam giác đều và tứ diện đều
Hình chóp tam giác đều có đáy là một tam giác đều, với ba mặt bên là các tam giác vuông cân. Ngược lại, tứ diện đều có bốn mặt là các tam giác đều, tất cả các cạnh của nó đều có độ dài bằng nhau. Sự khác biệt cơ bản giữa chúng là tứ diện đều có bốn mặt đối xứng hoàn hảo, trong khi hình chóp chỉ có ba mặt bên giống nhau.
Học sinh ngày nay không chỉ cần nắm vững khái niệm về hình chóp tam giác đều mà còn cần tìm hiểu thêm nhiều kiến thức học tập khác. Một chiếc điện thoại với cấu hình mạnh mẽ, dung lượng pin cao sẽ là công cụ hỗ trợ đắc lực giúp các em học tập và làm bài trực tuyến mọi lúc, mọi nơi. Mytour là cửa hàng lý tưởng đáp ứng mọi nhu cầu của học sinh với các chương trình ưu đãi hấp dẫn cho nhiều loại sản phẩm khác nhau. Khám phá ngay tại liên kết dưới đây nhé!
Hướng dẫn cách vẽ hình chóp tam giác đều đơn giản
Để vẽ hình chóp tam giác đều một cách đơn giản, bạn có thể làm theo các bước sau đây:
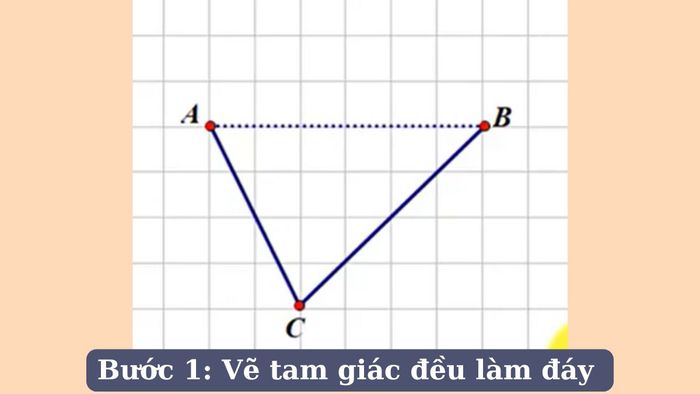
Bước 1 - Vẽ tam giác đều làm đáy: Đầu tiên, bạn vẽ một tam giác đều bằng cách kẻ ba cạnh có độ dài bằng nhau. Lưu ý rằng mỗi góc của tam giác đều phải có giá trị là 60 độ.
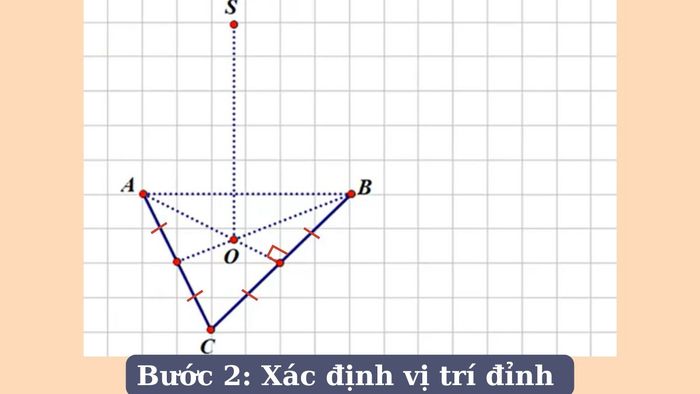
Bước 2 - Xác định vị trí đỉnh: Chọn một điểm trên trục thẳng đứng sao cho điểm này cách đều các đỉnh của tam giác đáy. Đây sẽ là đỉnh của hình chóp.
Bước 3 - Vẽ các mặt tam giác: Từ đỉnh đã xác định, vẽ ba đoạn thẳng nối đỉnh với ba đỉnh của tam giác đáy. Ba đoạn thẳng này sẽ tạo thành ba mặt tam giác vuông cân của hình chóp.
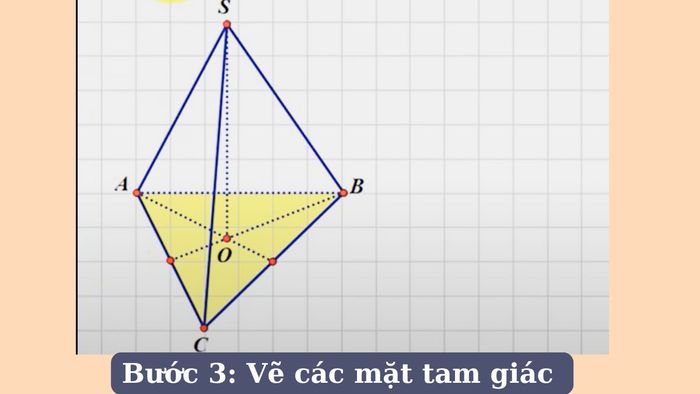
Các công thức tính liên quan đến hình chóp tam giác đều
Trước khi tìm hiểu các công thức tính toán, chúng ta cần hiểu rõ các thành phần cấu tạo nên hình chóp tam giác đều. Phần này sẽ giới thiệu các công thức tính diện tích xung quanh và thể tích, giúp bạn áp dụng vào các bài toán hình học một cách chính xác.
Công thức tính diện tích của hình chóp tam giác đều
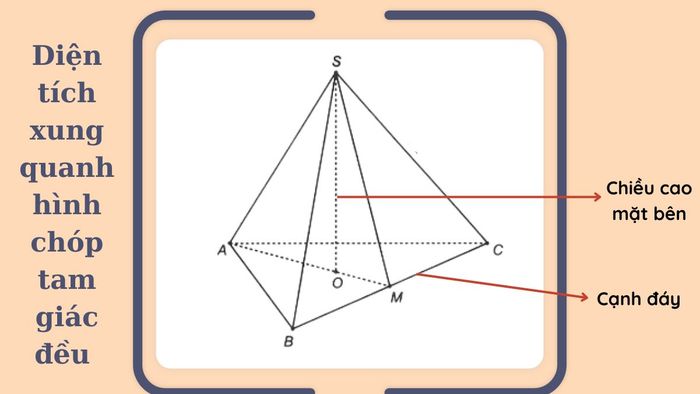
Diện tích xung quanh của hình chóp tam giác đều được tính bằng tổng diện tích của ba mặt tam giác bên. Bạn có thể áp dụng công thức sau để tính diện tích này:
Sxq = (3a x h_mặt) / 2
Trong đó:
- a là chiều dài cạnh của tam giác đáy.
- hmặt là chiều cao của mỗi mặt tam giác vuông cân (mặt bên) của hình chóp.
Việc sử dụng đúng công thức diện tích của hình chóp tam giác đều sẽ giúp bạn tính toán chính xác diện tích xung quanh của hình chóp, đây là yếu tố quan trọng khi giải quyết các bài toán hình học không gian.
Công thức tính thể tích hình chóp tam giác đều
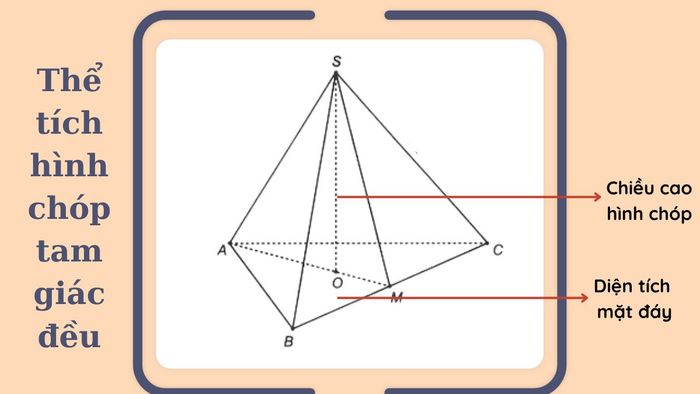
Thể tích của hình chóp tam giác đều được tính bằng công thức sau:
V = 1/3 x S(đáy) x h
Trong đó:
- S(đáy) = a²√3 / 4 là diện tích của đáy, với đáy là một tam giác đều.
- h là chiều cao của hình chóp, tính từ đáy đến đỉnh.
Việc áp dụng công thức tính thể tích hình chóp tam giác đều sẽ giúp bạn nhanh chóng giải quyết các bài toán về thể tích trong các bài toán hình học không gian.
Một số bài tập liên quan đến hình chóp tam giác đều
Bài tập 1: Tính thể tích hình chóp tam giác đều có cạnh đáy dài 6 cm và chiều cao 10 cm.
- Bước 1: Tính diện tích đáy. Vì đáy là tam giác đều có cạnh dài a = 6 cm, ta sử dụng công thức sau để tính diện tích đáy:
S(đáy) = (a²√3)/4 = (6²√3)/4 = 36√3/4 = 9√3 cm²
- Bước 2: Tính thể tích của hình chóp tam giác đều:
V = 1/3 x S(đáy) x h
Với S(đáy) = 9√3 cm² và h = 10 cm, ta tính được kết quả như sau:
V = 1/3 x 9√3 x 10 = 30√3 cm³
Bài tập 2: Tính diện tích xung quanh của hình chóp tam giác đều có cạnh đáy dài 8 cm và chiều cao mặt tam giác là 5 cm.
- Bước 1: Tính diện tích của mỗi mặt tam giác bên. Mỗi mặt tam giác bên có cạnh đáy a = 8 cm và chiều cao mặt tam giác hmặt = 5 cm. Diện tích của mỗi mặt tam giác vuông cân được tính bằng công thức:
Smặt bên = 1/2 x 8 x 5 = 20 cm²
- Bước 2: Tính diện tích xung quanh của hình chóp tam giác đều:
Sxq = 3 x Smặt bên = 3 x 20 = 60 cm²
Tóm lại, việc hiểu rõ các công thức tính thể tích và diện tích của hình chóp tam giác đều là điều cơ bản mà bạn cần ghi nhớ. Bên cạnh đó, việc nắm vững các thông tin về tính chất và cách vẽ hình chóp tam giác đều sẽ giúp bạn dễ dàng hình dung và giải quyết các bài toán. Đừng quên ghé thăm Mytour để tìm thêm thông tin bổ ích về giáo dục nhé.
