

| Set of regular p-gons | |
|---|---|
|
| |
| cạnh và các đỉnh | p |
| Công thức Schläfli | {p} |
| Coxeter–Dynkin diagram | |
| Nhóm đối xứng | Dihedral symmetry (Dp) |
| Dual polyhedron | Self-dual |
| Diện tích (with t=edge length) |
|
| Độ lớn của một góc trong (độ) |
|
| Tổng độ lớn của các góc trong (độ) |
|
Trong hình học Euclid, đa giác đều là loại đa giác có tất cả các cạnh và góc đều nhau. Đa giác đều được phân loại thành hai nhóm: đa giác lồi đều và đa giác sao đều.
Các đặc điểm chung
Những đặc điểm này áp dụng cho cả đa giác lồi đều và đa giác sao đều.
Mọi đỉnh của đa giác đều đều nằm trên một đường tròn, được gọi là các điểm đồng viên. Tất cả các đa giác đều đều có một đường tròn ngoại tiếp.
Với đặc tính các cạnh của đa giác đều có độ dài bằng nhau, điều này dẫn đến việc tất cả các đa giác đều đều có các đường tròn nội tiếp.
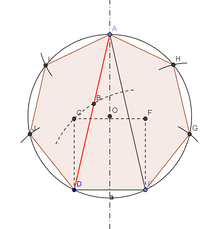
Một đa giác đều có n cạnh có thể được vẽ bằng compa và thước kẻ nếu và chỉ nếu các thừa số nguyên tố lẻ của n không phải là số nguyên tố Fermat.
Tính đối xứng
Nhóm đối xứng của đa giác đều bao gồm các hình vuông n D2, D3, D4,... Nó bao gồm sự quay quanh tâm Cn (tâm đối xứng), cùng với các trục đối xứng của n đi qua tâm này. Nếu n là số chẵn, một nửa số trục đối xứng sẽ đi qua hai đỉnh đối diện của đa giác, trong khi nửa còn lại đi qua trung điểm của hai cạnh đối diện. Nếu n là số lẻ, tất cả các trục đối xứng sẽ đi qua một đỉnh và trung điểm của cạnh đối diện với đỉnh đó.
Đa giác lồi đều
Tất cả các đa giác đơn (tức là đa giác không tự cắt) đều là đa giác lồi đều. Các đa giác có kích thước cạnh giống nhau thì được coi là đồng dạng.
Một đa giác lồi đều với n cạnh được mô tả bằng ký hiệu Schläfli là: {n}
- Đa giác 1 đỉnh: dạng suy biến trong không gian thông thường {1}
- Nhị giác đều: một 'đoạn thẳng đôi' - dạng suy biến trong không gian thông thường {2}
- Tam giác đều {3}
- Hình vuông {4}
- Ngũ giác đều {5}
- Lục giác đều {6}
- Thất giác đều {7}
- Bát giác đều {8}
- Cửu giác đều {9}
- Thập giác đều {10}



| Tam giác đều
|
Hình vuông
|
Ngũ giác đều
|
| Lục giác đều
|
Thất giác đều
|
Trong nhiều trường hợp, các đa giác được thảo luận đều là đa giác đều. Thường thì người ta bỏ qua từ đều. Ví dụ, mọi mặt của đa diện có thể là các hình đa giác đều như tam giác đều, hình vuông, ngũ giác đều, v.v.
Góc
Đối với một đa giác đều có n đỉnh, góc trong của nó được tính bằng công thức sau:
- (hoặc bằng ) độ,
hoặc độ radian,
hoặc vòng quay.
Mỗi góc ngoài (góc kề bù của góc trong) được tính bằng công thức độ, với tổng của các góc ngoài bằng 360 độ, hoặc 2π radian, hoặc một vòng quay.
Đường chéo
Khi , số lượng đường chéo được tính bằng công thức , với các giá trị như 0, 2, 5, 9,... Chúng chia đa giác thành 1, 4, 11, 24,... phần.
Diện tích
Diện tích A của một đa giác lồi đều có n cạnh được tính bằng công thức sau:
theo đơn vị độ
- ,
hoặc theo đơn vị radian ,
với t là độ dài của mỗi cạnh.
Nếu biết bán kính hoặc độ dài đoạn thẳng từ tâm đến một đỉnh, diện tích có thể được tính như sau: tính theo đơn vị độ
hoặc theo đơn vị radian
với r là bán kính của đa giác
Ngoài ra, diện tích cũng có thể tính bằng nửa chu vi nhân với độ dài của đoạn trung bình, a, (là đoạn vuông góc từ tâm đa giác hạ xuống một cạnh). Do đó, công thức là A = a.n.t/2, với chu vi là n.t, và có thể viết gọn hơn là 1/2 p.a.
Với mỗi cạnh t=1, ta có công thức sau:
tính theo độ
hoặc theo radian (với n không bằng 2)
Giá trị được trình bày trong bảng dưới đây:
| Số cạnh | tên hình | Diện tích chính xác | Xấp Xỉ |
|---|---|---|---|
| 3 | tam giác đều | 0.433 | |
| 4 | hình vuông | 1 | 1.000 |
| 5 | ngũ giác đều | 1.720 | |
| 6 | lục giác đều | 2.598 | |
| 7 | thất giác đều | 3.634 | |
| 8 | bát giác đều | 4.828 | |
| 9 | cửu giác đều | 6.182 | |
| 10 | thập giác đều | 7.694 | |
| 11 | đa giác đều 11 đỉnh | 9.366 | |
| 12 | đa giác đều 12 đỉnh | 11.196 | |
| 13 | đa giác đều 13 đỉnh | 13.186 | |
| 14 | đa giác đều 14 đỉnh | 15.335 | |
| 15 | đa giác đều 15 đỉnh | 17.642 | |
| 16 | đa giác đều 16 đỉnh | 20.109 | |
| 17 | đa giác đều 17 đỉnh | 22.735 | |
| 18 | đa giác đều 18 đỉnh | 25.521 | |
| 19 | đa giác đều 19 đỉnh | 28.465 | |
| 20 | đa giác đều 20 đỉnh | 31.569 | |
| 100 | đa giác đều 100 đỉnh | 795.513 | |
| 1000 | đa giác đều 1000 đỉnh | 79577.210 | |
| 10000 | đa giác đều 10000 đỉnh | 7957746.893 |
Các diện tích của đa giác đều nhỏ hơn diện tích của các hình tròn có cùng chu vi, với chênh lệch (làm tròn) là 0.26. Đối với n < 8, chênh lệch này cao hơn một chút (chênh lệch giảm dần khi n tăng, đến giới hạn là π/12).
Đa giác sao đều
Một đa giác đều không lồi được gọi là đa giác sao đều. Ví dụ điển hình nhất là hình sao 5 cánh, có cùng số đỉnh với ngũ giác đều nhưng các đỉnh được nối theo cách khác.
Đối với một đa giác sao n cạnh, công thức Schläfli được điều chỉnh để phù hợp với dạng sao m của đa giác, ví dụ như {n/m}. Nếu m bằng 2, mỗi đỉnh sẽ nối với hai đỉnh khác cách nó 2 đỉnh. Nếu m bằng 3, mỗi đỉnh nối với hai đỉnh khác cách nó 3 đỉnh. Đường biên của đa giác bao quanh tâm m lần, và m đôi khi được gọi là mật độ của đa giác sao đều.
Một số ví dụ tiêu biểu:
- Sao 5 cánh đều - {5/2}
- Sao 7 cánh đều - {7/2} và {7/3}
- Sao 8 cánh đều - {8/3}
- Sao 9 cánh đều - {9/2} và {9/4}
- Sao 10 cánh đều - {10/3}
- Sao 11 cánh đều - {11/2}, {11/3}, {11/4}, {11/5}
m và n cần phải là các số nguyên tố cùng nhau, nếu không hình sẽ bị suy biến. Tùy thuộc vào cách hiểu công thức Schläfli, có nhiều quan điểm khác nhau về các hình suy biến. Ví dụ, {6/2} có thể được hiểu theo hai cách:
- Vào thế kỉ 20, người ta thường dựng hình {6/2} bằng cách nối mỗi đỉnh của đa giác lồi đều {6} với các đỉnh cách nó 2 đỉnh, tạo thành một đa giác kép bao gồm 2 tam giác đều, hay còn gọi là hình sao 6 cánh đều.
- Nhiều nhà hình học hiện đại, như Grünbaum (2003), cho rằng cách hiểu này không chính xác. Họ coi /2 là chỉ việc di chuyển hai bước quanh {6} ở mỗi lần, tạo ra một tam giác 'gấp đôi' với hai đỉnh trùng nhau tại mỗi điểm góc và hai cạnh dọc theo mỗi đoạn thẳng. Cách này không chỉ phù hợp hơn với lý thuyết các đa diện trừu tượng hiện đại, mà còn giống hơn với cách Poinsot (1809) tạo ra các đa giác sao của ông - bằng cách dùng một đoạn dây và uốn nó tại các điểm liên tiếp qua cùng một góc cho đến khi hình khép kín.
- Coxeter, H. S. M. (1948), Đa diện đều, Methuen and Co.
- Grünbaum, B.; Các đa diện của bạn có giống với đa diện của tôi không?, Hình học rời rạc và tính toán: kỷ yếu Goodman-Pollack, Ed. Aronov và các cộng sự, Springer (2003), trang 461–488.
- Poinsot, L.; Ký sự về các đa giác và đa diện. J. de l'École Polytechnique 9 (1810), trang 16–48.
- Hình tròn
- Đa diện đều
- Đa diện đều trong không gian n chiều
- Hình cầu
Các liên kết bên ngoài
- Weisstein, Eric W., 'Đa giác đều', MathWorld.
- Mô tả Đa giác đều với hoạt hình tương tác
- Đường tròn nội tiếp của Đa giác đều với hoạt hình tương tác
- Diện tích của Đa giác đều Ba công thức khác nhau, kèm hoạt hình tương tác
- Các nghệ sĩ thời kỳ Phục hưng và các đa giác đều
