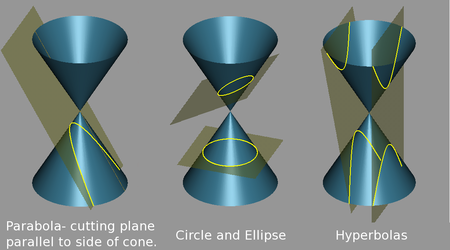
* Parabol
* Elíp và đường tròn
* Hyperbol
Trong toán học, một đường conic (hoặc gọi tắt là conic) là một đường cong bậc hai tạo nên bằng cách cắt một mặt nón tròn xoay bằng một mặt phẳng. Đường conic được nhắc đến và nghiên cứu 200 năm TCN, khi Apollonius của Pergaeus tiến hành một nghiên cứu có hệ thống về tính chất của các đường cô-níc.
Các định nghĩa
Đường cô-nic có thể được định nghĩa theo hai phương pháp khác nhau:
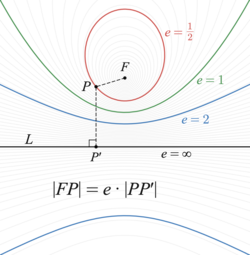
- Đường cô-nic là tổng hợp của các điểm mà tỷ lệ khoảng cách từ mỗi điểm đến điểm cố định F so với khoảng cách từ nó đến đường cố định L bằng giá trị cụ thể e.
- Đối với 0 < e < 1, kết quả là hình ellipse (nằm trên mặt phẳng vuông góc với đường L)
- Đối với e = 1 là parabol (nằm trên mặt phẳng chứa điểm F và đường L)
- Đối với e > 1 là hyperbol.
- Tại điểm cố định F gọi là tiêu điểm, đường thẳng cố định L gọi là đường chuẩn và giá trị cụ thể e gọi là tâm sai.
- Đường cô-nic là đường giao điểm giữa một mặt nón tròn xoay và một mặt phẳng. Khi mặt phẳng cắt qua hình nón và không song song với bất kỳ đường nào của nó, ta có một đường cong đóng, được gọi là ellipse. Nếu mặt phẳng song song với một đường của mặt nón, đường cô-nic sẽ trở thành parabol. Cuối cùng, nếu mặt phẳng cắt hai mặt nón có chung đỉnh (đồng thời cũng cắt hai đáy của hai hình nón này), ta có hai đường cong riêng biệt gọi là hyperbol.
Tên gọi đường cô-nic bắt nguồn từ việc cắt mặt nón tròn xoay này, với tên tiếng Anh của mặt nón là cone
Các đường Cô-níc
Dạng suy biến
Theo định nghĩa đầu tiên, có nhiều dạng suy biến của hình cô-nic, trong đó bao gồm trường hợp mặt phẳng đi qua đỉnh của hình chóp. Phần giao điểm trong trường hợp này có thể là một đường thẳng (khi mặt phẳng tiếp xúc với hình nón), một điểm (khi góc tạo bởi mặt phẳng với trục của hình nón lớn hơn góc tạo bởi mặt phẳng tiếp xúc với trục của hình nón), hoặc một cặp đường thẳng cắt nhau (khi góc đó nhỏ hơn).
Các điểm đặc biệt của Ellipse và Hyperbol
Hai bộ tiêu điểm và đường chuẩn
Đối với hình ellipse và hình hyperbol, tồn tại hai bộ tiêu điểm và đường chuẩn, hình thành một hình ellipse hoặc hyperbol hoàn chỉnh, đồng thời tạo ra tâm của hình (trung điểm của đoạn nối hai tiêu điểm). Theo định nghĩa này, hình ellipse và hình hyperbol có thể được định nghĩa một cách khác mà hình parabol không thể.
- Hình Ellipse là tổ hợp của các điểm M sao cho MF1+MF2=2a (hằng số), trong đó F1 và F2 là tiêu điểm.
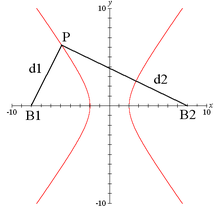
- Hình hyperbol là tổ hợp của các điểm M sao cho |MF1-MF2|=2a (hằng số), trong đó F1 và F2 là tiêu điểm.
Theo hai định nghĩa này, parabol có thể coi là dạng suy biến của hình ellipse khi tiêu điểm còn lại bị kéo dài ra vô cùng xa. Tương tự, hình tròn cũng có thể coi là dạng suy biến khi hai tiêu điểm của ellipse hợp lại thành một.
Trục chính (trục lớn) và trục phụ (trục nhỏ)
Ở hình ellipse và hình hyperbol có hai trục đối xứng, nhưng ở parabol chỉ có một.
- Ở hình ellipse, có trục lớn và trục bé. Trục lớn là đoạn đi qua hai tiêu điểm và tâm, trục bé là trục vuông góc với trục lớn tại tâm.
- Ở hình hyperbol, có trục thực và trục ảo. Trục thực là đoạn đi qua hai tiêu điểm, hai đỉnh của hai nhánh, và tâm. Trục ảo là trục vuông góc với trục thực tại tâm của hyperbol.
Qui ước: Độ dài trục lớn (trục thực) bằng giá trị không đổi 2a. Độ dài trục ảo (trục bé) bằng giá trị không đổi 2b. Trong đó, đối với ellipse và đối với hyperbol (F1F2=2c và được gọi là tiêu cự).
Hình chữ nhật cơ sở
- Trong hình hyperbol, hình chữ nhật cơ sở là hình chữ nhật có bốn đỉnh nằm trên hai đường tiệm cận. Trong bốn cạnh của hình chữ nhật, có hai cạnh là hai đường tiếp tuyến tiếp xúc với hai nhánh của hình hyperbol tại đỉnh của chúng, và tương ứng hai đỉnh này của hyperbol là hai trung điểm của hai cạnh. Hai cạnh đó song song với trục ảo và có chiều dài bằng trục ảo. Hai cạnh còn lại song song với trục thực và có độ dài bằng trục thực.
- Trong hình ellipse, hình chữ nhật cơ sở là hình ngoại tiếp ellipse. Tương tự như hình hyperbol: Trong bốn cạnh của hình chữ nhật, có hai cạnh là hai đường tiếp tuyến tiếp xúc với ellipse tại hai đỉnh (là các giao điểm của trục lớn với ellipse), và tương ứng hai đỉnh này của ellipse cũng là hai trung điểm của hai cạnh. Hai cạnh đó song song với trục ảo và có chiều dài bằng trục ảo. Hai cạnh còn lại song song với trục thực và có độ dài bằng trục thực.
Hệ tọa độ Descartes
Trong hệ tọa độ Descartes, hình ảnh của phương trình bậc hai hai ẩn luôn là một đường nón, và tất cả các đường nón đều có thể được biểu diễn dưới dạng này. Phương trình này có dạng
- với , , không đồng thời bằng 0.
Ta có:
- Nếu ( B^{2}-4AC < 0 ), phương trình cho ta một hình ellipse (trừ phi đường cô-nic bị suy biến, ví dụ như ( x^{2}+y^{2}+10=0 ));
Đồng thời nếu ( A=C ) và ( B=0 ), phương trình cho ta hình tròn;
Chú ý rằng A và B chỉ là các hệ số của đa thức, không phải là nửa độ dài của trục thực hay trục ảo.
Qua hệ trục tọa độ, các phương trình có thể được viết dưới dạng đơn giản:
- Đường tròn: ( x^{2}+y^{2}=r^{2} );
Ellipse: ( {x^{2} over a^{2}}+{y^{2} over b^{2}}=1 \)
Parabol: ( y^{2}=4ax \); Hyperbol: ( {x^{2} over a^{2}}-{y^{2} over b^{2}}=1 \); Hyperbol chữ nhật (hyperbol với hai đường tiệm cận vuông góc): ( xy=c^{2} \)
- Đường tròn: ,
Ma trận được gọi là ma trận đường cô-nic.
Đường cô-nic được gọi là định thức của đường cô-nic. Nếu Δ = 0 thì đường cô-nic suy biến, đường cô-nic trong thực tế chỉ còn là một cặp đường thẳng đồng nhất. Một đường cô-nic tự cắt chính nó luôn luôn là một dạng suy biến, mặc dù vậy không phải tất cả các dạng đường cô-nic suy biến đều tự cắt chính nó, nếu không cắt chính mình, chúng có dạng những đường thẳng.
Ví dụ như, đường cô-nic suy biến thành dạng cặp đường thẳng đồng nhất:
Một đường cô-nic đôi khi suy biến thành một đường thẳng đơn:
Tương tự như vậy, một đường cô-nic đôi khi suy biến thành một đường thẳng đơn:
Đường cô-nic có phương trình {\displaystyle \{x^{2}+2xy+y^{2}=0\}=\{(x+y)^{2}=0\}=\{x+y=0\}\cup \{x+y=0\}=\{x+y=0\}} được gọi là biệt thức của đường cô-nic.
Biệt thức δ của đường cô-nic là {\displaystyle \delta =\det \left({\begin{bmatrix}A_{1}&B_{1}\\B_{1}&A_{2}\end{bmatrix}}\right)}, nếu δ = 0 thì đường cô-nic là một parabol, nếu δ<0, nó là một hyperbol và nếu δ>0, nó là một hình ellipse. Đường cô-nic là một đường tròn nếu δ>0 và A1 = A2, là rectangular hyperbola nếu δ<0 và A1 = -A2.
Mỗi đường thẳng gặp mỗi đường cô-nic hai lần và được gọi là tiếp tuyến nếu giao điểm là một điểm kép. Mỗi đường cô-nic có hai điểm vô cực nếu những điểm đó là thật, đường cô-nic là một hyperbol, nếu chung là sự liên kết ảo, đường cô-nic là một hình ellipse, nếu có một điểm kép vô cực, nó là parabol. Nếu có một điểm thực vô cực hay hai điểm ảo không tạo ra sự liên kết, thì đường cô-nic không phải là ellipse, parabol hay hyperbol.
Đường cô-nic trong hệ tọa độ cực, với một tiêu điểm là gốc tọa độ và tiêu điểm còn lại nằm trên trục x, được xác định bởi công thức.
Trong hệ tọa độ cực, một đường cô-nic có một tiêu điểm là gốc tọa độ và tiêu điểm còn lại nằm trên trục x, được xác định bởi công thức.
- Trong phương trình r={l \over {1+e\cos \theta }}, với e là tâm sai và l bằng nửa độ dài cung đi qua một tiêu điểm và song song với đường chuẩn (xem phía dưới).
Như trên, với e = 0, ta có một đường tròn, với 0 e < 1 ta có một hình ellipse, với e = 1 một parabol, và với e > 1 một hyperbol.
Các thông số của đường cô-nic.
Các thông số biến thiên của các đường cô-nic được tổng hợp trong bảng sau.
| đường cô-nic | công thức | tâm sai (e) | Nửa tiêu cự (c) | nửa dây cung đi qua tiêu điểm song song với đường chuẩn (l) | khoảng cách từ tiêu điểm đến đường chuẩn (p)(p=l/e) |
|---|---|---|---|---|---|
| Đường tròn | |||||
| ellipse | , | ||||
| parabol | , | ||||
| hyperbol | , |
Các tính chất của đường cô-nic.
Đường cô-níc luôn có đặc tính 'trơn'. Cụ thể hơn, chúng không có bất kỳ điểm nào gây ra sự thay đổi về độ cong. Điều này rất quan trọng đối với nhiều ứng dụng của đường cô-níc, như trong khí động lực học, nơi tính trơn của bề mặt giúp ngăn chặn sự không đều của không khí hoặc nước trong quá trình di chuyển.
Các ứng dụng quan trọng của đường cô-níc
Đường cô-níc đóng vai trò quan trọng trong thiên văn học: quỹ đạo của hai vật thể tương tác được mô tả bởi luật vạn vật hấp dẫn của Newton có thể là các đường cô-níc nếu chúng tự do. Nếu chúng di chuyển về cùng một hướng, chúng tạo thành hình elip; nếu chúng di chuyển tách biệt, chúng có thể là hình parabol hoặc hyperbol. Trong hình học phản xạ, đường cô-níc trên mặt phẳng phản xạ tương đương với các đường khác trong các biến đổi hình học phản xạ.
Để hiểu rõ hơn về các ứng dụng đặc biệt của mỗi loại đường cô-níc, hãy tham khảo các bài viết về hình elip, parabol, và hyperbol.
Ghi chú quan trọng
- Akopyan, A.V. và Zaslavsky, A.A. (2007). Hình học của đường cô-níc. Hội Toán học Mỹ. tr. 134. ISBN 0821843230.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- Hyperbol
- Parabol
- Hình elip
- Đường tròn
- Đường bậc ba
- Mặt bậc hai
- Một số định lý liên quan đến đường cô-níc
Liên kết ngoài
- Các phương pháp dẫn xuất của đường cô-níc tại
- Các đường cô-níc tại Đặc tính đường cong mặt phẳng đặc biệt.
- Đường cô-níc trên MathWorld
- Định thức và các đường cong đường cô-níc
- Đường cô-níc xuất hiện. Các đường cô-níc trong tự nhiên và ở những nơi khác Lưu trữ 2006-04-06 tại Wayback Machine.
- Các đường cô-níc Lưu trữ 2007-10-06 tại Wayback Machine.
Đường cô-níc tại trang PlanetMath.org.
