Hình elip

Trong toán học, một hình elip là một đường cong phẳng có hai tiêu điểm, sao cho tổng khoảng cách từ bất kỳ điểm nào trên đường cong đến hai tiêu điểm luôn bằng một hằng số. Hình tròn là một trường hợp đặc biệt của hình elip khi hai tiêu điểm trùng nhau. Độ dẹt của hình elip được đo bằng tâm sai e, dao động từ e = 0 (hình tròn) đến e = 1 (hình parabol với độ dẹt vô hạn).

Phương trình chuẩn của một hình elip với tâm tại gốc tọa độ và chiều dài 2a cùng chiều rộng 2b được mô tả như sau:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$

Nếu a ≥ b, các tiêu điểm có tọa độ (±c, 0) với $c=\sqrt{a^2-<!--\; -\; -->b^2}$. Phương trình tham số của hình elip là:

$(x,y)=(a\cos <!--\; \; -->(t),b\sin <!--\; \; -->(t\left)\right)0\le <!--\; \le \; -->t\le <!--\; \le \; -->2\mathrm{\pi <!--\; \pi \; -->}.$

Hình elip là một dạng đường conic kín, tức là một đường cong phẳng được hình thành khi cắt một hình nón bằng một mặt phẳng nghiêng (như hình minh họa). Nó có nhiều điểm tương đồng với hai loại đường conic khác là parabol và hyperbol, cả hai đều không đóng và không có giới hạn. Hơn nữa, một mặt cắt nghiêng của hình trụ tròn cũng tạo ra hình elip.

Một hình elip cũng có thể được mô tả qua một tiêu điểm và một đường thẳng nằm ngoài elip, gọi là đường chuẩn. Elip là quỹ tích của các điểm mà tỉ lệ khoảng cách giữa điểm đó và tiêu điểm với khoảng cách tới đường chuẩn luôn không thay đổi. Tỉ lệ này chính là tâm sai của elip được xác định như sau:

$e=\frac{c}{a}=\sqrt{1-<!--\; -\; -->\frac{b^2}{a^2}}$.

Hình elip có nhiều ứng dụng quan trọng trong các lĩnh vực vật lý, thiên văn và kỹ thuật. Ví dụ, quỹ đạo của các hành tinh trong hệ Mặt Trời gần như là hình elip với Mặt Trời nằm tại một tiêu điểm (thực chất là tâm tỉ cự của cặp Mặt Trời và hành tinh). Quỹ đạo của mặt trăng quanh hành tinh và tất cả các hệ thiên thể khác cũng tuân theo nguyên tắc này. Hình dạng của các hành tinh và sao thường được mô tả bằng hình ellipsoid. Một hình tròn khi nhìn từ một góc nghiêng sẽ trở thành hình elip, tức là hình elip là kết quả của việc chiếu hình tròn qua phép chiếu song song hoặc vuông góc. Hình elip còn là dạng đường cong Lissajous đơn giản nhất, với các chuyển động ngang và dọc đều là hình sin có cùng tần số. Hiện tượng tương tự còn dẫn đến phân cực elip của ánh sáng trong quang học.

Nguồn gốc từ ngữ

Thuật ngữ 'elip' (tiếng Anh: ellipse) xuất phát từ tiếng Hy Lạp cổ đại: ἔλλειψις (élleipsis, có nghĩa là 'thiếu'), được đặt ra bởi nhà toán học Apollonius xứ Perga trong tác phẩm Conics của ông.

Khái niệm về quỹ tích

Một đường elíp có thể được mô tả như tập hợp các điểm trên mặt phẳng Euclid:

Với hai điểm cố định F₁, F₂ gọi là tiêu điểm và một khoảng cách 2a lớn hơn khoảng cách giữa hai tiêu điểm, elíp là quỹ tích của các điểm P sao cho tổng khoảng cách từ P đến hai tiêu điểm F₁ và F₂ luôn bằng 2a. Tức là

$E=\left\{P\in <!--\; \in \; -->R^2:|P{F}_1|+|P{F}_2|=2a\right\}.$

Trung điểm C của đoạn thẳng nối hai tiêu điểm được gọi là tâm của elíp. Đoạn thẳng nối hai tiêu điểm được gọi là trục lớn, trong khi đoạn thẳng vuông góc với trục lớn và đi qua tâm được gọi là trục bé. Các trục của elíp cắt elíp tại bốn điểm, được gọi là các đỉnh của elíp. Đoạn thẳng F₁F₂ = 2c được gọi là tiêu cự, và c là bán tiêu cự. Tỉ số e = c / a được gọi là độ lệch tâm hoặc tâm sai.

Khi F₁ ≡ F₂, ta có một đường tròn, là trường hợp đặc biệt của elíp.

Phương trình | PF₁ | + | PF₂ | = 2a có thể được hiểu theo cách khác như sau:

Nếu c₂ là đường tròn với tâm tại F₂ và bán kính 2a, thì quỹ tích của các điểm P có khoảng cách từ P đến đường tròn c₂ bằng khoảng cách từ P đến tiêu điểm F₁ chính là một đường elíp:

$E=\left\{P\in <!--\; \in \; -->R^2:|P{F}_1|=|P{c}_2|\right\}.$

Đường tròn c₂ được gọi là đường tròn chuẩn (với tâm là tiêu điểm F₂) của elíp. Bên cạnh đó, còn một định nghĩa phổ biến khác của elíp sử dụng đường chuẩn, được mô tả dưới đây.

Nhờ vào mặt cầu Dandelin, ta có thể chứng minh rằng bất kỳ mặt cắt nghiêng của một hình nón đều là một hình elíp, miễn là mặt phẳng cắt không đi qua đỉnh và có độ nghiêng nhỏ hơn độ nghiêng của đường sinh trên mặt nón.

Hệ tọa độ Descartes

Phương trình chính tắc

Trong phần còn lại của bài viết, (E) biểu thị hình elíp trong hệ tọa độ Descartes với tâm nằm tại gốc tọa độ, trục lớn song song với trục x và

Các tiêu điểm của elíp là F₁ = (c, 0) và F₂ = (−c, 0),

Các đỉnh của elíp là V₁ = (a, 0) và V₂ = (−a, 0),

trong đó a > c.

Với một điểm có tọa độ (x, y) nằm trên elíp (E), khoảng cách từ điểm đó đến tiêu điểm (c, 0) được tính bằng $\sqrt{(x-<!--\; -\; -->c{)}^2+y^2}$, và khoảng cách đến tiêu điểm còn lại là $\sqrt{(x+c{)}^2+y^2}$. Do điểm (x, y) thuộc elíp nên

$\sqrt{(x-<!--\; -\; -->c{)}^2+y^2}+\sqrt{(x+c{)}^2+y^2}=2a.$

Khi thực hiện các phép biến đổi phù hợp và đặt ẩn phụ b = a − c, ta có được phương trình chính tắc của elip (E):

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

(1)

Khi giải phương trình để tìm giá trị của y, ta có kết quả

$y=\pm <!--\; \pm \; -->\frac{b}{a}\sqrt{a^2-<!--\; -\; -->x^2}=\pm <!--\; \pm \; -->\sqrt{\left(a^2-<!--\; -\; -->x^2\right)\left(1-<!--\; -\; -->e^2\right)}.$

Các kích thước a và b của elíp được gọi là bán trục lớn và bán trục bé. Khoảng cách từ một điểm (x, y) đến các tiêu điểm trái và phải lần lượt là a + ex và a − ex.

Từ phương trình này, dễ dàng nhận thấy rằng elíp có tính đối xứng qua các trục tọa độ cũng như qua gốc tọa độ.

Xác minh phương trình chính tắc

Dựa vào phương trình tổng khoảng cách

$\sqrt{(x-<!--\; -\; -->c{)}^2+y^2}+\sqrt{(x+c{)}^2+y^2}=2a$

Chuyển một dấu căn sang bên kia rồi bình phương hai vế, ta có được

$(x-<!--\; -\; -->c{)}^2+y^2=4a^2+(x+c{)}^2+y^2-<!--\; -\; -->4a\sqrt{(x+c{)}^2+y^2}$

Rút gọn phương trình trên cho ta

Rút gọn và sắp xếp lại phương trình trên ta có:

$a^2(a^2-<!--\; -\; -->c^2)=(a^2-<!--\; -\; -->c^2)x^2+a^2{y}^2$

Đặt b = a − c và chia cả hai vế của phương trình cho (ab), ta sẽ thu được phương trình chính tắc của elip.

Trong toàn bộ bài viết này, a được coi là bán trục lớn và b là bán trục bé, với điều kiện a ≥ b > 0. Trong phương trình chính tắc của elip (1), nếu a < b, elip sẽ có dạng dài hơn là dạng dẹt.

Bán tiêu cự c là khoảng cách từ một tiêu điểm đến tâm của elip: $c=\sqrt{a^2-<!--\; -\; -->b^2}$.

Độ lệch tâm hay còn gọi là tâm sai e được xác định là

$e=\frac{c}{a}=\sqrt{1-<!--\; -\; -->{\left(\frac{b}{a}\right)}^2}$,

với điều kiện a > b. Nếu elip có hai trục bằng nhau (a = b), nó trở thành một đường tròn với tâm sai bằng 0. Ngược lại, nếu trục bé bằng 0, elip trở thành một parabol với tâm sai bằng 1.

Đoạn dây qua một tiêu điểm và vuông góc với trục lớn được gọi là trục bên (tiếng Anh: latus rectum). Một nửa của trục bên là bán trục bên, ký hiệu là ℓ, và có giá trị bằng

$\mathrm{\ell <!--\; \ell \; -->}=\frac{b^2}{a}=a\left(1-<!--\; -\; -->e^2\right).$

Bán trục bên ℓ chính là bán kính cong của đường tròn tiếp xúc với elip tại các đỉnh của trục lớn.

Tiếp tuyến

Một đường thẳng d cắt elip tại hai điểm gọi là cát tuyến, hoặc tại một điểm gọi là tiếp tuyến. Phương trình của tiếp tuyến tại điểm (x₁, y₁) của elip (E) là:

$\frac{x_1}{a^2}x+\frac{y_1}{b^2}y=1.$

Phương trình tham số của tiếp tuyến tại điểm này là:

$\{\begin{array}{c}x=x_1-<!--\; -\; -->y_1{a}^{2}t\\ y=y_1+x_1{b}^{2}t\end{array}(t\in <!--\; \in \; -->R)$

Hoặc có thể viết dưới dạng vector như sau:

$\stackrel{\to <!--\; \to \; -->}{d}=(x_1,y_1)+t(-<!--\; -\; -->y_1{a}^2,x_1{b}^2).$

Nếu hai điểm trên elip (x₁, y₁) và (x₂, y₂) thỏa mãn điều kiện $\frac{x_1{x}_2}{a^2}+\frac{y_{1}v}{b^2}=0$, thì chúng nằm trên hai đường kính liên hợp (xem ở dưới). Nếu a = b, elip trở thành hình tròn và trong trường hợp này, hai đường kính sẽ vuông góc với nhau.

Chứng minh

Xét điểm (x₁, y₁) nằm trên elíp (E) và $\stackrel{\to <!--\; \to \; -->}{d}=(x_1,y_1)+t(u,v)$ là phương trình của một đường thẳng g đi qua điểm (x₁, y₁). Vì vậy, một điểm P nằm trên đường thẳng g có tọa độ (x₁ + tu, y₁ + tv). Giả sử điểm P cũng nằm trên elíp (E). Thay tọa độ của P vào phương trình chính tắc của elíp (1), ta có

Vậy ta có hai trường hợp sau đây:

1. $\frac{x_1}{a^2}u+\frac{y_1}{b^2}$ Đây là điều kiện t = 0, nghĩa là điểm (x₁, y₁) chính là điểm tiếp xúc. Nói cách khác, đường thẳng g chỉ chạm vào elíp tại điểm (x₁, y₁), và do đó, g là tiếp tuyến tại điểm đó. Vecto pháp tuyến của g là $\left(\begin{array}{c}\frac{x_1}{a^2},\frac{y_1}{b^2}\end{array}\right)$, vì vậy phương trình của tiếp tuyến là $\frac{x_1}{a^2}x+\frac{y_1}{b^2}y=k$ với một hằng số k nào đó. Vì điểm (x₁, y₁) nằm trên tiếp tuyến này, thay vào phương trình ta được k = 1.
2. $\frac{x_1}{a^2}u+\frac{y_1}{b^2}v\ne <!--\; \ne \; -->0.$ Trong trường hợp này, đường thẳng g cắt elíp tại hai điểm khác nhau, với giá trị $t=0$ và $t=-<!--\; -\; -->2\left(\frac{x_{1}u}{a^2}+\frac{y_{1}v}{b^2}\right){\left(\frac{u^2}{a^2}+\frac{v^2}{b^2}\right)}^{-<!--\; -\; -->1}.$ Điều này cho thấy g là một cát tuyến của elíp (E).

Tâm của elíp không phải là gốc tọa độ

Khi elíp có tâm tại (x₀, y₀), phương trình chuẩn của nó là:

$\frac{{\left(x-<!--\; -\; -->x_0\right)}^2}{a^2}+\frac{{\left(y-<!--\; -\; -->y_0\right)}^2}{b^2}=1.$

Các trục của elíp vẫn song song với các trục x và y.

Elíp ở dạng tổng quát

Trong hình học giải tích, elíp là một mặt bậc hai: tập hợp các điểm $(X,Y)$ trên mặt phẳng Descartes thỏa mãn phương trình bậc hai

$A{X}^2+BXY+C{Y}^2+DX+EY+F=0$

(2)

Điều kiện cần thiết là

Để phân biệt với trường hợp suy biến, ta định nghĩa Δ là định thức

Khi đó, elíp là một elíp thực (tức (2) có nghiệm thực) và không suy biến khi và chỉ khi C∆ < 0. Nếu C∆ > 0, phương trình không có nghiệm thực, và nếu ∆ = 0, elíp trở thành một điểm.

Nếu một elíp có bán trục lớn là a, bán trục nhỏ là b, tọa độ tâm là (x₀, y₀), và góc quay là ϕ (góc từ trục x dương đến bán trục lớn của elíp), thì các hệ số của phương trình (2) được tính như sau:

$$

A = a 2 ( sin ⁡ ϕ ) 2 + b 2 ( cos ⁡ ϕ ) 2 B = ( b 2 − a 2 ) sin ⁡ 2 ϕ C = a 2 ( cos ⁡ ϕ ) 2 + b 2 ( sin ⁡ ϕ ) 2 D = − 2 A x 0 − B y 0 E = − B x 0 − 2 C y 0 F = A x 0 2 + B x 0 y 0 + C y 0 2 − a 2 b 2 . {\displaystyle {\begin{aligned}A&=a^{2}(\sin \phi )^{2}+b^{2}(\cos \phi )^{2}\\B&=\left(b^{2}-a^{2}\right)\sin 2\phi \\C&=a^{2}(\cos \phi )^{2}+b^{2}(\sin \phi )^{2}\\D&=-2Ax_{0}-By_{0}\\E&=-Bx_{0}-2Cy_{0}\\F&=Ax_{0}^{2}+Bx_{0}y_{0}+Cy_{0}^{2}-a^{2}b^{2}.\end{aligned}}}

Các biểu thức này có thể được rút ra từ phương trình elíp chuẩn $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ bằng cách biến đổi tọa độ affine.

Ngược lại, từ phương trình tổng quát (2) có thể suy luận ra phương trình chuẩn theo cách sau:

Biểu diễn dưới dạng tham số

Biểu diễn tham số chính thức

Sử dụng các hàm lượng giác, biểu diễn tham số của elíp chuẩn $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ là:

Tham số t (hay còn gọi là dị thường lệch tâm trong thiên văn học) không phải là góc tạo bởi điểm (x(t), y(t)) và trục hoành, mà là tham số có ý nghĩa hình học do Philippe de La Hire đề xuất (xem Vẽ elíp dưới đây).

Biểu diễn theo cách hữu tỉ

Sử dụng phép đổi biến $u=\tan <!--\; \; -->\left(\frac{t}{2}\right)$, ta có các biểu thức hữu tỉ cho các hàm lượng giác:

$\cos <!--\; \; -->t=\frac{1-<!--\; -\; -->u^2}{u^2+1},\sin <!--\; \; -->t=\frac{2u}{u^2+1}$

và hệ phương trình tham số hữu tỉ của elíp

Hệ phương trình này mô tả tất cả các điểm trên elíp chính tắc $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ trừ đỉnh bên trái (−a, 0).

Khi $u\in <!--\; \in \; -->[0,1]$, công thức này mô tả góc phần tư thứ nhất (phần trên bên phải) của elíp, di chuyển ngược chiều kim đồng hồ khi u tăng lên. Đỉnh bên trái (−a, 0) là giới hạn $\underset{u\to <!--\; \to \; -->\pm <!--\; \pm \; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}\left(x\right(u),y(u\left)\right).$

Các dạng hữu tỉ của đường conic thường được áp dụng trong phần mềm CAD, chẳng hạn như đường cong Bézier.

Độ dốc tiếp tuyến dưới dạng tham số

Một cách biểu diễn tham số khác dựa vào độ dốc m của tiếp tuyến tại điểm (a cos t, b sin t). Độ dốc này có thể được tính từ đạo hàm của phương trình tham số đã cho, cụ thể như sau:

Dựa vào các đẳng thức lượng giác, ta có thể tính toán như sau:

$\cos <!--\; \; -->t=\frac{\cot <!--\; \; -->t}{\pm <!--\; \pm \; -->\sqrt{1+{\cot }^2<!--\; \; -->t}}=\frac{-<!--\; -\; -->ma}{\pm <!--\; \pm \; -->\sqrt{m^2{a}^2+b^2}},\sin <!--\; \; -->t=\frac{1}{\pm <!--\; \pm \; -->\sqrt{1+{\cot }^2<!--\; \; -->t}}=\frac{b}{\pm <!--\; \pm \; -->\sqrt{m^2{a}^2+b^2}}.$

Thay thế các biểu thức của cos t và sin t vào phương trình tham số chuẩn, ta có được:

$\{\begin{array}{c}x=\frac{-<!--\; -\; -->m{a}^2}{\pm <!--\; \pm \; -->\sqrt{m^2{a}^2+b^2}}\\ y=\frac{b^2}{\pm <!--\; \pm \; -->\sqrt{m^2{a}^2+b^2}}\end{array}m\in <!--\; \in \; -->R.$

Ở đây, m là độ dốc của tiếp tuyến tại điểm trên elíp. Khi dấu trong căn thức là dương, điểm (x, y) nằm ở nửa trên của elíp, còn nếu dấu âm thì điểm nằm ở nửa dưới. Hai đỉnh bên trái và phải (±a, 0) không được biểu diễn vì có tiếp tuyến thẳng đứng (độ dốc là vô cực).

Phương trình tiếp tuyến tại điểm (x(m), y(m)) có dạng y = mx + n. Hệ số tự do n có thể được xác định bằng cách thay tọa độ của điểm trên elíp vào phương trình, cho kết quả:

$y=mx\pm <!--\; \pm \; -->\sqrt{m^2{a}^2+b^2}.$

Phương trình tiếp tuyến này có thể được sử dụng để xác định các trục của hình elíp.

Elíp tổng quát

Một cách định nghĩa khác cho elíp là thông qua biến đổi affine, như sau:

Mọi elíp đều là ảnh của một phép biến đổi affine từ đường tròn đơn vị với phương trình $x^2+y^2=1$.

Biểu diễn theo tham số

Một phép biến đổi affine trên mặt phẳng Euclid có dạng $\stackrel{\to <!--\; \to \; -->}{x}\mapsto <!--\; \mapsto \; -->\stackrel{\to <!--\; \to \; -->}{f}{}_0+A\stackrel{\to <!--\; \to \; -->}{x}$, với A là một ma trận (có định thức khác không) và $\stackrel{\to <!--\; \to \; -->}{f}{}_0$ là một vectơ cố định. Nếu $\stackrel{\to <!--\; \to \; -->}{f}{}_1,\stackrel{\to <!--\; \to \; -->}{f}{}_2$ là các vectơ cột của ma trận A, thì đường tròn đơn vị (cos(t), sin(t)), với 0 ≤ t ≤ 2π, sẽ trở thành hình elíp:

$\stackrel{\to <!--\; \to \; -->}{x}=\stackrel{\to <!--\; \to \; -->}{p}\left(t\right)=\stackrel{\to <!--\; \to \; -->}{f}{}_0+\stackrel{\to <!--\; \to \; -->}{f}{}_1\cos <!--\; \; -->t+\stackrel{\to <!--\; \to \; -->}{f}{}_2\sin <!--\; \; -->t.$

(3)

Ở đây $\stackrel{\to <!--\; \to \; -->}{f}{}_0$ là trung tâm và $\stackrel{\to <!--\; \to \; -->}{f}{}_1,\stackrel{\to <!--\; \to \; -->}{f}{}_2$ là hướng của hai đường kính liên hợp, không nhất thiết phải vuông góc.

Đỉnh

Bốn đỉnh của elíp là $\stackrel{\to <!--\; \to \; -->}{p}\left(t_0+k\frac{\mathrm{\pi <!--\; \pi \; -->}}{2}\right),k=0,1,2,3$, với tham số t₀ là nghiệm của:

$\cot <!--\; \; -->\left(2t_0\right)=\frac{\stackrel{\to <!--\; \to \; -->}{f}{}_1^2-<!--\; -\; -->\stackrel{\to <!--\; \to \; -->}{f}{}_2^2}{2\stackrel{\to <!--\; \to \; -->}{f}{}_1\cdot <!--\; \cdot \; -->\stackrel{\to <!--\; \to \; -->}{f}{}_2}.$

(Nếu $\stackrel{\to <!--\; \to \; -->}{f}{}_1\cdot <!--\; \cdot \; -->\stackrel{\to <!--\; \to \; -->}{f}{}_2=0$, thì t₀ = 0.) Từ đây, ta suy ra được phương trình sau. Vectơ tiếp tuyến tại điểm $\stackrel{\to <!--\; \to \; -->}{p}\left(t\right)$ là:

$\stackrel{\to <!--\; \to \; -->}{p}{}^{\prime }\left(t\right)=-<!--\; -\; -->\stackrel{\to <!--\; \to \; -->}{f}{}_1\sin <!--\; \; -->t+\stackrel{\to <!--\; \to \; -->}{f}{}_2\cos <!--\; \; -->t.$

Tại các đỉnh của elíp với tham số t = t₀, các tiếp tuyến với elíp sẽ vuông góc với các bán trục lớn và nhỏ, do vậy:

Khi ta khai triển và áp dụng các công thức lượng giác cos t − sin t = cos 2t, 2sin t cos t = sin 2t, ta nhận được phương trình như trên.

Phương trình ẩn

Giải phương trình với các tham số cos t, sin t bằng quy tắc Cramer và với điều kiện cos t + sin t = 1, ta có được phương trình ẩn.

.

Elíp trong không gian ba chiều

Định nghĩa chung của elíp ở đây giúp ta mô tả các tham số của bất kỳ elíp nào, kể cả trong không gian ba chiều, khi ta có các vectơ trong không gian.

Hệ tọa độ cực

Hệ tọa độ cực với điểm gốc tại tâm của elíp

Trong hệ tọa độ cực, khi gốc tọa độ là tâm của elíp và góc θ đo từ bán trục chính, phương trình của elíp được viết như sau

Hệ tọa độ cực đối với tiêu điểm

Nếu ta sử dụng hệ tọa độ cực với điểm gốc là một trong các tiêu điểm của elíp, và góc θ đo từ bán trục chính, phương trình của elíp sẽ là

Trong đó, dấu cộng hoặc trừ ở mẫu số phụ thuộc vào hướng của θ = 0 so với tâm elíp: dấu âm khi hướng về tâm và dấu dương khi hướng ra xa.

Trong trường hợp tổng quát hơn, nếu elíp có một tiêu điểm tại gốc tọa độ và tiêu điểm còn lại ở tọa độ góc φ, phương trình cực của elíp là:

Góc θ trong các công thức trên được gọi là dị thường thực của điểm xem xét. Tử số ℓ = a(1 − e) đại diện cho bán trục bên.

Độ lệch tâm và đường chuẩn

Hai đường thẳng song song, cách nhau một đoạn bằng d = a / c = a / e, được gọi là đường chuẩn của elíp.

Với bất kỳ điểm P nào trên elíp, tỷ lệ giữa khoảng cách đến một tiêu điểm và khoảng cách đến đường chuẩn tương ứng chính là độ lệch tâm của elíp:

Chúng ta có thể chứng minh điều này cho cặp F₁, l₁. Lưu ý rằng ${\left|P{F}_1\right|}^2=(x-<!--\; -\; -->c{)}^2+y^2,{\left|P{l}_1\right|}^2={\left(x-<!--\; -\; -->\frac{a^2}{c}\right)}^2$ và $y^2=b^2-<!--\; -\; -->\frac{b^2}{a^2}{x}^2$ thỏa mãn phương trình

Điều này cũng đúng ngược lại và thường được dùng để định nghĩa elíp qua đường chuẩn, tương tự như định nghĩa của parabol.

Với tiêu điểm F và đường chuẩn l không đi qua F, và một số thực e với điều kiện 0 < e < 1, elíp là tập hợp các điểm sao cho tỷ lệ khoảng cách từ điểm đó đến tiêu điểm và đến đường chuẩn bằng e. Hay nói cách khác, $E=\left\{P:|PF|/|Pl|=e\right\}.$

Khi e = 0, tức là tâm sai của đường tròn, ta coi đường chuẩn của đường tròn nằm ở vô cực. Nếu e = 1, quỹ tích trở thành hình parabol, và nếu e > 1, ta có hình hyperbol.

Chứng minh

Giả sử F = (f, 0) và đường chuẩn l có phương trình x = −f / e, với e > 0. Khi đó, gốc tọa độ (0, 0) nằm trên đường cong. Giả sử điểm P = (x, y) thỏa mãn | PF | = e | Pl |. Sau khi biến đổi, ta có phương trình:

$x^2\left(e^2-<!--\; -\; -->1\right)+2x(1+e)f-<!--\; -\; -->y^2=0.$

Đây là phương trình của một elíp khi e < 1, của một parabol khi e = 1, hoặc của một hyperbol khi e > 1. Cả ba loại đường conic này đều có gốc tọa độ làm đỉnh.

Khi e < 1, chọn hai số a, b sao cho 1 − e = (b / a) và p = b / a. Khi đó, phương trình trên trở thành

Đây là phương trình của một elíp với tâm tại (a, 0), trục chính theo phương hoành và bán trục lớn và nhỏ lần lượt là a, b.

Elíp tổng quát

Nếu tiêu điểm là F = (f₁, f₂) và đường chuẩn có phương trình ax + by + c = 0, phương trình elíp sẽ là:

Các tính chất phản xạ

Elíp có những đặc điểm sau đây:

Khi điểm P nằm trên elíp, pháp tuyến tại P sẽ chia đôi góc $\stackrel{^<!--\; ^\; -->}{F_{1}P{F}_2}.$ (Trong trường hợp này, pháp tuyến là đường vuông góc với tiếp tuyến tại điểm đó)

Chứng minh

Chúng ta sẽ chứng minh rằng tiếp tuyến chính là đường phân giác ngoài của tam giác PF₁F₂.

Chọn điểm L trên tia F₂P sao cho LF₂ = 2a, với a là bán trục lớn của elíp. Đặt đường thẳng w là phân giác ngoài tại đỉnh P của tam giác PF₁F₂. Để chứng minh rằng w là tiếp tuyến tại P, hãy chọn một điểm Q khác P trên w, và chứng minh rằng Q không nằm trên elíp. Do đó, đường thẳng w chỉ cắt elíp tại điểm P, xác nhận rằng w là tiếp tuyến tại P.

Dựa vào hình vẽ và áp dụng bất đẳng thức tam giác, ta có , từ đó suy ra: $\left|Q{F}_2\right|+\left|Q{F}_1\right|>2a.$ Nếu Q nằm trên elíp thì tổng này phải bằng 2a. Vì vậy, điểm Q không thuộc elíp, chứng minh hoàn tất.

Ứng dụng

Những tia phát xuất từ một tiêu điểm của elíp khi phản chiếu về tiêu điểm còn lại dẫn đến các ứng dụng trong quang học và âm thanh, tương tự như tính chất phản chiếu của parabol (xem hiệu ứng phòng thì thầm).

Đường kính liên hợp

Đường tròn có đặc điểm như sau:

Trung điểm của các dây cung song song nằm trên một đường kính của đường tròn.

Đường kính đó vuông góc với các dây cung song song. Qua phép biến đổi afin, tính chất song song và trung điểm của các đoạn thẳng được bảo toàn, do đó tính chất này cũng áp dụng cho elíp. Tuy nhiên, trong trường hợp này, đường kính và các dây cung song song không vuông góc với nhau. Đường kính liên hợp của elíp có thể coi là sự mở rộng của đường kính vuông góc trong đường tròn.

Định nghĩa

Hai đường kính d₁, d₂ của elíp được gọi là liên hợp nếu trung điểm của các dây cung song song với d₁ nằm trên d₂.

Từ hình minh họa, chúng ta có thể thấy rằng:

Hai đường kính P₁Q₁, P₂Q₂ của elíp là liên hợp nếu và chỉ nếu tiếp tuyến tại P₁ (hoặc Q₁) song song với P₂Q₂.

Trong phương trình tham số của elíp tổng quát (3) đã nêu trên:

Bất kỳ hai điểm tạo thành một đường kính. Cặp tạo thành đường kính liên hợp của nó.

Định lý Apollonius về đường kính liên hợp

Xét một elíp với hai bán trục a, b. Giả sử c₁, c₂ là hai bán kính liên hợp của elíp, tương đương với một nửa của đường kính liên hợp. Khi đó, ta có:

1. $c_1^2+c_2^2=a^2+b^2$,
2. hình bình hành tạo bởi các tiếp tuyến với đường kính liên hợp có diện tích A = 4ab.

Định lý đầu tiên trong số này được gọi là định lý Apollonius về đường kính liên hợp, trong khi công thức tính diện tích là định lý Apollonius thứ hai.

Chứng minh

Giả sử elíp có dạng chuẩn (với tâm tại gốc tọa độ, hai bán trục tương ứng với trục hoành và trục tung), có phương trình tham số như sau:

.

Hai điểm là hai đường kính liên hợp (như đã đề cập trước đó). Từ công thức lượng giác, ta có . Sau khi thực hiện các biến đổi đại số, ta có thể chứng minh rằng:

Diện tích của tam giác tạo thành bởi và dây cung nối hai điểm này là:

Theo hình vẽ, diện tích của hình bình hành ngoại tiếp elíp gấp 8 lần diện tích tam giác, do đó diện tích của hình bình hành là 4ab.

Đặc điểm đo lường

Tất cả các tính chất dưới đây áp dụng cho elíp có phương trình

Diện tích

Diện tích của elíp $A_{\text{elip}}$ là:

$A_{\text{elip}}=\mathrm{\pi <!--\; \pi \; -->}ab$

Trong đó a và b là các bán trục lớn và nhỏ của elíp. Công thức này rất tự nhiên: bắt đầu từ một vòng tròn có bán kính b và diện tích πb, rồi kéo dài theo tỉ số $a/b$ để tạo ra elíp. Việc kéo dài này làm tăng diện tích theo tỉ số tương ứng: $\mathrm{\pi <!--\; \pi \; -->}{b}^2\left(a/b\right)=\mathrm{\pi <!--\; \pi \; -->}ab.$ Chúng ta cũng có thể chứng minh tính chất này bằng tích phân như sau.

Phương trình (1) có thể được viết lại thành $y\left(x\right)=b\sqrt{1-<!--\; -\; -->x^2/a^2},$ với $x\in <!--\; \in \; -->[-<!--\; -\; -->a,a],$ đường cong này là nửa trên của elíp. Do đó, diện tích của elíp bằng hai lần tích phân của y(x) trên đoạn [−a, a]:

Tích phân thứ hai chính là diện tích của một vòng tròn có bán kính a, và bằng πa. Do đó

Một elíp với phương trình $A{x}^2+Bxy+C{y}^2=1$ có diện tích $2\mathrm{\pi <!--\; \pi \; -->}/\sqrt{4AC-<!--\; -\; -->B^2}.$

Chu vi

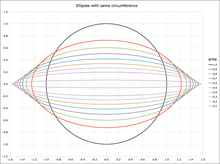
Chu vi của một elíp, ký hiệu là C, được tính bằng:

$C=4a{\int <!--\; \int \; -->}_0^{\mathrm{\pi <!--\; \pi \; -->}/2}\sqrt{1-<!--\; -\; -->e^2{\sin }^2<!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}}d\mathrm{\theta <!--\; \theta \; -->}=4aE\left(e\right)$

Trong đó a là chiều dài của bán trục lớn, $e=\sqrt{1-<!--\; -\; -->b^2/a^2}$ là độ lệch của elíp, và E là hàm tích phân elliptic đầy đủ loại II,

$E\left(e\right)={\int <!--\; \int \; -->}_0^{\mathrm{\pi <!--\; \pi \; -->}/2}\sqrt{1-<!--\; -\; -->e^2{\sin }^2<!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}}d\mathrm{\theta <!--\; \theta \; -->}.$

Chuỗi vô hạn của công thức này được cho bởi:

Trong đó n!! là giai thừa kép. Chuỗi này hội tụ, nhưng khi đặt h = (a − b) / (a + b), James Ivory và Bessel đã phát hiện một công thức khác hội tụ nhanh hơn nhiều.

Srinivasa Ramanujan đã đưa ra hai phương pháp xấp xỉ cho chu vi trong phần §16 của 'Các Phương Trình Modular và Xấp Xỉ của π':

$C\approx <!--\; \approx \; -->\mathrm{\pi <!--\; \pi \; -->}\left(3(a+b)-<!--\; -\; -->\sqrt{(3a+b)(a+3b)}\right),$

và

Những sai số của các xấp xỉ này lần lượt tương ứng với cấp độ của h và h.

Một số bất đẳng thức liên quan đến chu vi của elíp chuẩn x / a + y / b = 1 với a ≥ b bao gồm

Chặn trên của chu vi là 2πa, tương ứng với chu vi của đường tròn ngoại tiếp đi qua hai đỉnh của trục lớn elíp. Chặn dưới là $4\sqrt{a^2+b^2}$, chu vi của hình thoi nối bốn đỉnh của elíp.

Độ cong

Độ cong của elíp được xác định bởi công thức

Bán kính cong tại điểm (x, y) là:

Bán kính cong tại các đỉnh (±a, 0) và tại tâm cong là:

Bán kính cong tại các đỉnh (0, ±b) và tại tâm cong là:

• Hình elíp
• Hình elíp Descartes, dạng tổng quát của elíp
• Các định luật Kepler về chuyển động của các thiên thể
• Hình nón tiếp xúc và nội tiếp
• Hệ tọa độ elíp, hệ tọa độ vuông góc dựa trên elíp và hyperbol
• Phương trình vi phân riêng phần của elíp
• Hình cầu, hình ellipsoid tạo ra bằng cách xoay elíp quanh trục lớn hoặc bé
• Siêu elíp, dạng tổng quát khác của elíp
• Dị thường đúng, dị thường tâm sai, và dị thường trung bình

Chú thích

• Besant, W.H. (1907). “Chương III. Hình elíp”. Các Đoạn Conic. London: George Bell and Sons. tr. 50.
• Coxeter, H.S.M. (1969). Giới thiệu về Hình học (ấn bản 2). New York: Wiley. tr. 115–9.
• Meserve, Bruce E. (1983) [1959], Các Khái Niệm Cơ Bản về Hình học, Dover, ISBN 978-0-486-63415-9
• Miller, Charles D.; Lial, Margaret L.; Schneider, David I. (1990). Các Nguyên Tắc Đại số Cao đẳng (ấn bản 3). Scott Foresman/Little. tr. 381. ISBN 978-0-673-38638-0.
• Protter, Murray H.; Morrey, Charles B., Jr. (1970), Tính Toán Cao Đẳng với Hình học Phân tích (ấn bản 2), Reading: Addison-Wesley, LCCN 76087042

Liên kết ngoài

• Hình elíp (toán học) trên Encyclopædia Britannica (tiếng Anh)
• Hình elíp tại PlanetMath.org.
• Weisstein, Eric W., 'Hình elíp' từ MathWorld.
• Weisstein, Eric W., 'Hình elíp như trường hợp đặc biệt của hypotrochoid' từ MathWorld.
• Phát sinh Hình elíp của Apollonius tại Convergence
• Hình dạng và Lịch sử của Hình elíp tại Washington, D.C. của Clark Kimberling
• Công cụ tính chu vi hình elíp
• Danh sách các bản trình diễn hình elíp động
• Ivanov, A.B. (2001), “Hình elíp”, trong Hazewinkel, Michiel (biên tập), Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4