Hình học tập hợp là một nhóm các điểm trong không gian, thỏa mãn một thuộc tính hay đặc điểm nào đó.
Các loại hình học tập hợp cơ bản (trong mặt phẳng):
- Tập hợp các điểm gồm hai điểm A, B và tất cả những điểm nằm giữa A và B là đoạn thẳng AB.
- Tập hợp các điểm cách đều hai điểm cố định là đường trung trực của đoạn thẳng nối hai điểm đó.
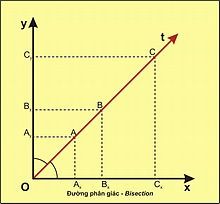
- Tập hợp các điểm cách đều hai cạnh của một góc là tia phân giác của góc đó.
- Tập hợp các điểm cách đường thẳng d một khoảng bằng L là hai đường thẳng song song với d và cách d một khoảng bằng L.
- Tập hợp các điểm cách điểm cố định O một khoảng bằng r là đường tròn tâm O, bán kính r trong mặt phẳng và là mặt cầu tâm O, bán kính r trong không gian ba chiều.
- Tập hợp các điểm M tạo thành với hai đầu mút của đoạn thẳng AB một góc AMB có số đo bằng α không đổi là hai cung tròn đối xứng qua AB (gọi là cung tròn chứa góc α vẽ trên đoạn AB).
- Đặc biệt: Tập hợp các điểm luôn nhìn hai điểm cố định A, B dưới một góc vuông là đường tròn đường kính AB.
- Tập hợp các điểm nằm sau một đường thẳng là một nửa mặt phẳng có bờ là đường thẳng đó.
- Tập hợp các cặp điểm đối xứng qua một đường thẳng là mặt phẳng chứa đường thẳng đó.
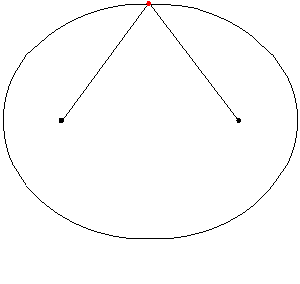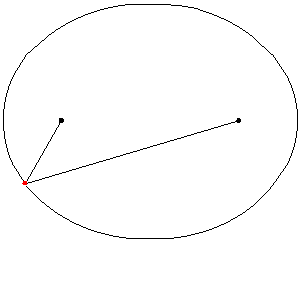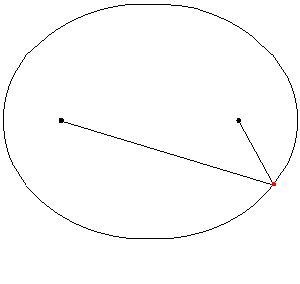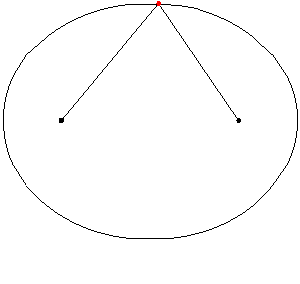
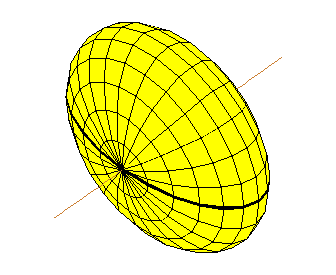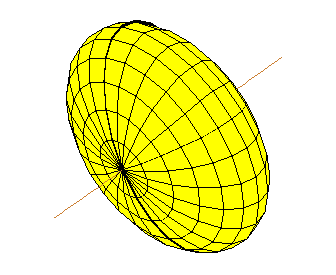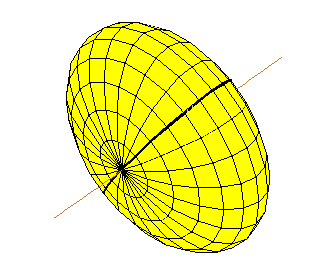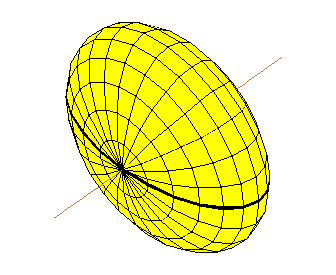
- Tập hợp các điểm trong mặt phẳng có tổng khoảng cách tới hai điểm cố định là đường elíp với hai tiêu điểm là hai điểm đó; trong không gian ba chiều là mặt Ellipsoid tròn xoay.
- Tập hợp các điểm cách đều một điểm và một đường thẳng cố định là đường Parabol trong mặt phẳng; trong không gian ba chiều là mặt Paraboloid tròn xoay.
Đường Parabol
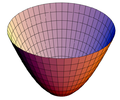
Paraboloid xoay tròn
- Tập hợp các điểm trong mặt phẳng có trị tuyệt đối của hiệu khoảng cách tới hai điểm cố định là đường hyperbol với hai tiêu điểm là hai điểm đó
