Trong không gian ba chiều, hình nón được tạo ra khi một đường thẳng l di chuyển dọc theo một đường cong ω và luôn xuyên qua một điểm cố định P.
Đường cong ω được gọi là đường tựa, còn đường thẳng l là đường sinh, và điểm P là đỉnh của hình nón. Nếu ω là một đường cong phẳng và khép kín, phần mặt phẳng bị giới hạn bởi ω (gọi là đáy) sẽ có trọng tâm, và đường thẳng nối đỉnh P với trọng tâm của ω là trục của hình trụ.
Khi đỉnh P di chuyển ra xa vô tận, hình nón sẽ chuyển thành hình trụ.
Các dạng hình nón
Mặt nón bậc hai elliptic là tập hợp các điểm trong không gian có tọa độ Đề-các thỏa mãn phương trình dưới đây:
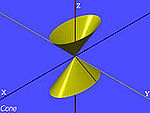
|
|
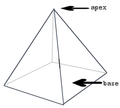
Khi đường tựa ω là một đa giác, chúng ta có mặt nón hình kim tự tháp. Nếu đường tựa ω là một đường thẳng, hoặc là một đường cong phẳng nằm cùng mặt phẳng với đỉnh P, mặt nón sẽ trở thành mặt phẳng.
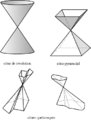
Mặt nón có thể được mở rộng từ dạng thực thành dạng ảo.
Đường cong bậc hai
Khi đường tựa là một đường tròn và điểm chiếu của đỉnh P trùng với tâm đường tròn, ta thu được mặt nón tròn xoay.
Khi một mặt phẳng cắt mặt nón tròn xoay, nếu đỉnh của mặt nón không nằm trên mặt phẳng cắt, giao tuyến sẽ là một đường cong bậc hai, thường gọi là đường conic theo tên tiếng Anh của mặt nón là cone:
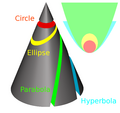

- Mặt phẳng vuông góc với trục nón: tạo ra đường tròn.
- Mặt phẳng cắt qua trục của nón và các đường sinh, hoặc mặt phẳng cắt tất cả các đường sinh của nón: tạo ra đường elip.
- Mặt phẳng song song với một đường sinh: tạo ra đường parabol.
- Mặt phẳng song song với hai đường sinh của nón: tạo ra đường hyperbol.
Hình nón
Khi thay đường thẳng l bằng đoạn thẳng SK với điểm S cố định và điểm K di chuyển trên đường cong ω, ta sẽ có khối hình được giới hạn bởi mặt nón quét bởi SK và đường cong ω. Trong trường hợp này, SK được gọi là đường sinh, S là đỉnh của hình nón, và mặt phẳng giới hạn bởi ω là đáy của nón.
Chiều cao của hình nón chính là khoảng cách từ đỉnh đến mặt đáy.
Diện tích xung quanh hình nón
Diện tích xung quanh của hình nón tròn xoay được tính bằng nửa tích của độ dài đường tròn đáy với độ dài đường sinh.
Thể tích
Thể tích của hình nón được tính bằng một phần ba tích của chiều cao (h) và diện tích của mặt đáy ():
Hình nón phổ biến nhất có đáy là hình tròn. Trong trường hợp này, nếu r là bán kính của đáy tròn, thể tích của hình nón được tính bằng:
- Mặt trụ
- Mặt bậc hai
- Nón lồi
- Mặt tròn xoay
Liên kết ngoài
- ^ “Công Ty Quà Tặng Doanh Nghiệp Cone - Cần Quà Là Có Nè”. Công Ty Quà Tặng Doanh Nghiệp Cone - Cần Quà Là Có Nè. Truy cập ngày 14 tháng 12 năm 2023.
