Tam giác Pascal, trong toán học, là một cấu trúc hình tam giác chứa các hệ số nhị thức. Mặc dù nó được đặt theo tên nhà toán học Pháp Blaise Pascal, nhiều nhà toán học ở Ấn Độ, Ba Tư (Iran), Trung Quốc, Đức và Ý đã nghiên cứu nó từ hàng thế kỷ trước.
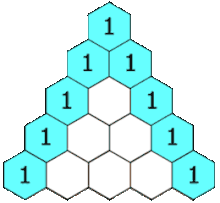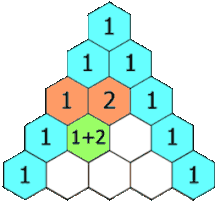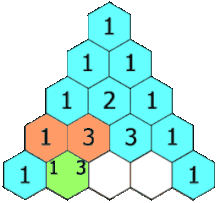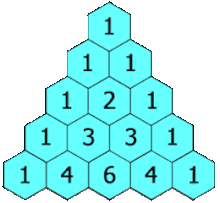
Tam giác Pascal được tổ chức theo hàng, bắt đầu từ hàng n = 0 ở đỉnh. Các phần tử trong mỗi hàng được đánh số từ trái sang phải với k = 0 và thường được đặt lệch so với các hàng bên cạnh. Để xây dựng tam giác, bắt đầu với số 1 duy nhất ở hàng 0. Các số trong các hàng sau được tính bằng cách cộng số ở trên bên trái với số ở trên bên phải, coi những ô trống là 0. Ví dụ: số đầu tiên ở hàng đầu tiên là 1 (tổng của 0 và 1), và các số 1 và 3 trong hàng thứ ba được cộng lại để tạo ra số 4 ở hàng thứ tư.
Công thức
Mỗi ô trong hàng thứ n và cột thứ k của tam giác Pascal được biểu thị bằng ký hiệu . Ví dụ, ô duy nhất ở hàng trên cùng là . Với ký hiệu này, việc xây dựng tam giác có thể được mô tả như sau:
- ,
đối với mọi số nguyên không âm n và mọi số nguyên k nằm trong khoảng từ 0 đến n, bao gồm cả hai đầu. Quy tắc này gọi là quy tắc sinh của tam giác Pascal.
Đề cập đến phân phối nhị thức và kết quả
Khi chia mỗi hàng của tam giác Pascal cho 2, nó trở thành phân phối nhị thức đối xứng với p = 1/2. Theo định lý giới hạn trung tâm, phân phối này dần tiếp cận phân phối chuẩn khi n tăng. Điều này có thể chứng minh bằng cách áp dụng Công thức Stirling cho các yếu tố trong công thức kết hợp.
Điều này liên quan đến hoạt động của tích chập rời rạc theo hai cách. Trước tiên, phép nhân đa thức chính xác tương ứng với tích chập rời rạc, liên tục tạo ra chuỗi {..., 0, 0, 1, 1, 0, 0, ...} tương ứng với việc lấy lũy thừa 1 + x, tạo ra các hàng của tam giác. Thứ hai, liên tục kết hợp hàm phân phối cho một biến ngẫu nhiên tương ứng với việc tính toán hàm phân phối cho tổng số bản sao độc lập n của biến đó; đây chính là tình huống mà định lý giới hạn trung tâm áp dụng, dẫn đến phân phối chuẩn trong giới hạn.
Liên kết ngoài
- Weisstein, Eric W., 'Tam giác Pascal' từ MathWorld.
- Biểu đồ phương pháp cổ của Bảy Bình phương Nhân (từ Ssu Yuan Yü Chien của Chu Shi-Chieh, 1303, mô tả chín hàng đầu tiên của tam giác Pascal)
- Triển khai Tam giác Pascal bằng Java – bao gồm chuyển đổi các chữ số cao hơn thành chữ số đơn.
- Luận văn của Pascal về Tam giác Số Học Lưu trữ 2004-08-03 tại Wayback Machine (hình ảnh trang của luận văn Pascal, 1655; tóm tắt Lưu trữ 2004-08-03 tại Wayback Machine)
- Các Sử Dụng Sớm Nhất Của Một Số Từ Ngữ Toán Học (P)
- Leibniz và tam giác Pascal
- Mẫu chấm, Tam giác Pascal, và Định lý Lucas
- Omar Khayyam nhà toán học Lưu trữ 2011-08-14 tại Wayback Machine
- Thông tin về Tam giác Pascal
- Giải thích về Tam giác Pascal và các trường hợp phổ biến, bao gồm liên kết đến phiên bản tương tác chỉ định số hàng muốn xem
- Triển khai Tam giác Pascal trong SQL Lưu trữ 2018-10-02 tại Wayback Machine
