1. Hình thang cân là gì?
Hình thang cân là một tứ giác có hai cạnh đối diện song song và hai góc kề một cạnh đáy bằng nhau.
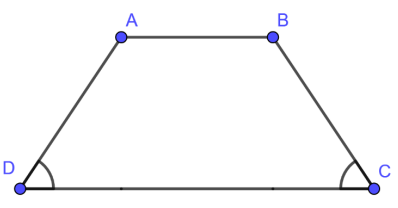
Ví dụ: Trong hình thang cân ABCD với các đáy AB và CD, ta có AB // CD và góc C bằng góc D.
2. Đặc điểm của hình thang cân
.jpg)
Đặc điểm của hình thang cân bao gồm:
- Định lý 1: Hai cạnh bên của hình thang cân là bằng nhau
Ví dụ: Trong hình thang cân ABCD với các đáy AB và CD, ta có AD = BC.
- Định lý 2: Các góc kề một cạnh đáy của hình thang cân là bằng nhau
Ví dụ: Trong hình thang cân ABCD với các đáy AB và CD, ta có AC = BD.
- Định lý 3: Hai đường chéo của hình thang cân là bằng nhau
Ví dụ: Trong hình thang cân ABCD với các đáy AB và CD, ta có góc C bằng góc D và góc A bằng góc B.
Khi một hình thang cân được nội tiếp trong một đường tròn, điều đó có nghĩa là tất cả bốn đỉnh của hình thang cân đều nằm trên đường tròn.
3. Cách nhận diện và chứng minh hình thang cân
3.1. Cách nhận diện hình thang cân
- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
- Hình thang có thể nội tiếp trong một đường tròn là hình thang cân.
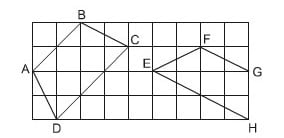
Ví dụ: Trong các tứ giác ABCD và EFGH được vẽ trên giấy kẻ ô, tứ giác nào là hình thang cân? Giải thích lý do.
Giải đáp:
Để xác định tứ giác nào là hình thang cân, cần áp dụng các tính chất của hình thang cân: (1) Hai cạnh bên của hình thang bằng nhau; (2) Hai góc kề một đáy bằng nhau; (3) Hai đường chéo của hình thang bằng nhau.
Với hai tứ giác được vẽ trên giấy kẻ ô, bạn có thể dễ dàng so sánh độ dài của các cạnh bên bằng mắt thường, từ đó nhận diện tứ giác nào là hình thang cân dựa trên các tính chất trên.
Theo đó:
- Tứ giác ABCD là hình thang cân vì AD = BC (cả hai đều là đường chéo của các tam giác có các cạnh bằng nhau)
- Tứ giác EFGH không phải là hình thang cân vì EF > GH (đường chéo của tam giác lớn hơn cạnh của tam giác đó)
Chú ý:
Hình thang cân có hai cạnh bên bằng nhau, nhưng điều ngược lại không phải lúc nào cũng đúng. Ví dụ, tứ giác có hai cặp cạnh song song cũng có thể có các cạnh bên bằng nhau, nhưng không nhất thiết là hình thang cân.
3.2. Phương pháp chứng minh hình thang cân
Phương pháp chứng minh một hình thang là hình thang cân
- Để chứng minh một hình thang có hai góc kề một đáy bằng nhau là hình thang cân, bạn cần chỉ ra rằng nó thỏa mãn điều kiện của hình thang cân.
- Để chứng minh một hình thang có hai đường chéo bằng nhau là hình thang cân, bạn cần xác nhận rằng điều này phù hợp với định nghĩa của hình thang cân.
4. Một số bài tập về hình thang cân
4.1. Bài tập 1: Chứng minh hình thang cân
VD1: Trong hình thang ABCD với AB // CD và góc ACD bằng góc BDC. Hãy chứng minh rằng hình thang ABCD là hình thang cân.
Giải pháp:
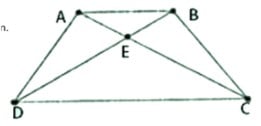
Đặt E là điểm giao nhau của hai đường chéo AC và BD.
Vì góc ACD bằng góc BCD nên tam giác ECD là tam giác cân với hai góc C1 và D1 bằng nhau, dẫn đến EC = ED. (1)
Tương tự, vì góc ACD bằng góc BCD và AB // CD nên tam giác EAB cũng là tam giác cân tại E, suy ra EA = EB. (2)
Từ (1) và (2), ta có: EA + EC = EB + ED, do đó AC = BD
Hình thang ABCD có hai đường chéo bằng nhau, điều này chứng minh rằng hình thang ABCD là hình thang cân.
VD2: Xét hình thang cân ABCD (với AB // CD), E là điểm giao nhau của hai đường chéo. Chứng minh rằng EA = EB và EC = ED.
Lời giải:

Vì ABCD là hình thang cân (theo giả thiết), do đó AD = BC và AC = BD (theo đặc điểm của hình thang cân)
Xem xét các tam giác ADC và BCD với các thông tin sau:
AD = BC (đã chứng minh trước đó)
AC = BD (đã chứng minh trước đó)
DC là cạnh chung
=> Tam giác ADC đồng dạng với tam giác BCD (theo cạnh-cạnh-cạnh)
Suy ra góc ACD = góc BDC (hai góc tương ứng)
Do đó, tam giác EDC là tam giác cân tại E (dựa vào dấu hiệu tam giác cân) => EC = ED (tính chất của tam giác cân)
Ngoài ra, chúng ta có: AC = BD (đã chứng minh trước đó), EC = ED (đã chứng minh trước đó)
=> AC - CE = BD - ED => EA = EB
Vậy ta có EA = EB và EC = ED (như yêu cầu chứng minh).
VD 3: Cho tam giác cân ABC với đỉnh A, và các đường phân giác BD, CE (D nằm trên AC, E nằm trên AB). Chứng minh rằng tứ giác BEDC là hình thang cân, với đáy nhỏ bằng cạnh bên.
Để chứng minh một tứ giác là hình thang cân, chúng ta cần thực hiện 2 bước:
- Bước 1: Xác định tứ giác đó là hình thang bằng cách sử dụng các tính chất của tứ giác có hai cạnh song song. Để chứng minh cạnh song song, có thể dùng các phương pháp như: (1) Hai góc đồng vị bằng nhau, (2) Hai góc so le trong bằng nhau, (3) Hai góc trong cùng phía bù nhau, (4) Định lý từ vuông góc đến song song.
- Bước 2: Xác minh rằng hình thang đó là hình thang cân.
Lời giải:
Tam giác ABC là tam giác cân tại A (giả thiết), do đó AB = AC và góc ABC bằng góc ACB (tính chất của tam giác cân).
Vì BD và CE lần lượt là các phân giác của góc ABC và góc ACB (theo giả thiết), nên dựa vào tính chất của tia phân giác:
Góc B1 bằng góc B2, mỗi góc đều bằng một nửa góc ABC.
Góc C1 bằng góc C2, mỗi góc đều bằng một nửa góc ACB.
Vì góc ABC bằng góc ACB (như đã chứng minh) nên góc B1 = góc B2 = góc C1 = góc C2.
Xem xét tam giác ABD và tam giác ACE với các điều kiện: (1) AB = AC, (2) Góc A là chung, (3) Góc B1 = góc C1 (như đã chứng minh) => ta có tam giác ABD = tam giác ACE theo tiêu chí góc - cạnh - góc.
=> AD = AE (do hai cạnh tương ứng bằng nhau).
Vì AD = AE (như đã chứng minh), nên tam giác ADE là tam giác cân tại A (dấu hiệu nhận biết tam giác cân) => góc AED = góc ADE (tính chất của tam giác cân).
Xem tam giác ADE, ta có: góc AED + góc ADE + góc A = 180 độ (định lý tổng ba góc trong tam giác) => góc AED = (180 độ - góc A) / 2 (1).
Xem tam giác ABC, ta có: góc A + góc ABC + góc ACB = 180 độ (định lý tổng ba góc trong tam giác) => góc ABC = (180 độ - góc A) / 2 (2).
Từ (1) và (2) => góc AED = góc ABC. Vì hai góc này là các góc đồng vị, nên ta kết luận DE // BC.
Vậy tứ giác BEDC là một hình thang.
Thêm vào đó, góc ABC = góc ACB (như đã chứng minh).
=> BEDC là một hình thang cân.
Có DE // BC => góc D1 = góc B2 (do hai góc so le trong).
Hơn nữa, góc B2 = góc B2 (như đã chứng minh trước đó), do đó góc B1 = góc D1.
=> Tam giác EBD là tam giác cân tại E.
=> EB = ED.
Vậy tứ giác BEDC là một hình thang cân, với đáy nhỏ bằng cạnh bên.
4.2. Bài tập 2: Tính diện tích của hình thang cân.
Để tính diện tích của hình thang cân, bạn có thể áp dụng công thức tính diện tích hình thang thông thường.
Diện tích của hình thang được tính bằng cách nhân chiều cao với trung bình cộng của hai đáy.
Để tính diện tích hình thang,
ta cần cộng chiều dài của đáy lớn và đáy nhỏ lại với nhau,
rồi nhân tổng này với chiều cao của hình thang.
Chia đôi và lấy một nửa sẽ cho kết quả tương tự.
.jpg)
4.3. Bài tập 3: Tính chu vi của hình thang cân
Giả sử có hình thang cân ABCD với hai đáy AB và CD có độ dài lần lượt là a và b, và độ dài của cạnh bên là c. Chu vi của hình thang cân ABCD sẽ được tính như sau:
P = a + b + 2c
Ví dụ: Cho tam giác ABC cân tại đỉnh A. Trên các cạnh AB và AC, lần lượt chọn các điểm D và E sao cho AD = AE.
a) Chứng minh rằng tứ giác BDEC là hình thang cân
b) Tính các góc của hình thang cân đó, biết rằng góc A = 50 độ.
Hướng dẫn giải
a) Vì tam giác ABC cân tại A nên AB = AC và theo giả thiết AD = AE, từ đó suy ra DB = EC
=> Tứ giác BDEC là hình thang cân
b) Vì tam giác ABC cân tại đỉnh A nên hai góc B và C bằng nhau
Tổng các góc trong tam giác ABC là 180 độ, do đó góc B = góc C = (180 độ - 50 độ) / 2 = 65 độ
Vì BDEC là hình thang cân nên góc BDE = góc DEC
Tổng các góc trong tứ giác BDEC là 360 độ, do đó góc B + góc C + góc BDE = góc DEC = 360 độ
=> Góc BDE và góc DEC đều bằng (360 - 2 x 65) / 2 = 115 độ
Trên đây là toàn bộ nội dung về hình thang cân từ Mytour. Hy vọng bài viết đã mang đến cho quý bạn đọc những kiến thức bổ ích. Cảm ơn sự quan tâm của các bạn.
