Hình thang vuông là gì? Khám phá định nghĩa, đặc điểm và cách nhận diện

1. Hình thang vuông là gì?

Hình thang là một tứ giác có hai cạnh đối song song, và các cạnh song song này được gọi là các cạnh đáy của hình thang.

Hình thang vuông là một hình thang có một góc vuông, và là một dạng đặc biệt của hình thang. Hình thang vuông có vai trò quan trọng trong toán học và đời sống, vì vậy việc hiểu rõ khái niệm về hình thang vuông là rất cần thiết.

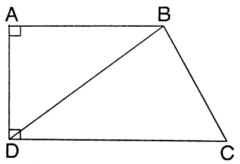
Hình minh họa cho hình thang vuông

2. Cách nhận diện và các đặc điểm, tính chất của hình thang vuông

*Nhận diện hình thang vuông

Một tứ giác với hai cạnh song song là hình thang

Hình thang có một góc vuông chính là hình thang vuông.

*Các đặc điểm và tính chất của hình thang vuông

- Nếu một hình thang có hai cạnh bên song song, thì hai cạnh này không chỉ song song mà còn bằng nhau.

- Nếu hai cạnh đáy của hình thang bằng nhau, thì các cạnh bên song song cũng sẽ bằng nhau.

- Hình thang vuông có những đặc điểm cơ bản của hình thang như hai cạnh đáy song song, và thêm vào đó, có một góc vuông giữa hai cạnh đáy tạo thành góc 90 độ.

3. Các công thức tính toán liên quan đến hình thang vuông bạn cần biết

* Công thức tính diện tích của hình thang vuông

Công thức tính diện tích của hình thang vuông tương tự như công thức tính diện tích của hình thang. Cụ thể là: tính trung bình cộng của hai cạnh đáy và nhân với chiều cao giữa hai đáy.

Lưu ý: Chiều cao ở đây chính là cạnh bên vuông góc với cả hai đáy.

Diện tích của hình thang vuông có thể được tính bằng một nửa tích của tổng hai đáy và chiều cao tương ứng với hai cạnh đáy hoặc bằng tích của chiều cao và trung bình cộng của hai đáy

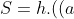
Trong đó:

- S là diện tích của hình thang

- a và b là độ dài của hai cạnh đáy

- h là độ dài của cạnh bên vuông góc với hai đáy.

Để tính diện tích của một hình thang vuông một cách chính xác, bạn có thể thực hiện theo các bước sau đây:

Bước 1: Xác định chiều dài của hai đáy của hình thang vuông, lần lượt gọi là a và b.

Bước 2

Bước 3: Áp dụng công thức tính diện tích hình thang vuông để tính toán diện tích

Ví dụ: Hình thang ABCD (AB // CD) có AB = 4 cm, CD = 8 cm và AD = 5 cm. Tính diện tích của hình thang ABCD.

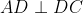
Do đó, AD chính là chiều cao của hình thang.

Diện tích của hình thang ABCD được tính như sau:

*Công thức tính chu vi hình thang vuông

Để tính chu vi của một hình thang vuông, bạn làm theo cách tính chu vi của hình thang thông thường, tức là cộng tổng các cạnh bên và đáy 

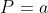
Trong đó:

- P: Chu vi của hình thang

- a, b: Độ dài của hai cạnh đáy

- c, d: Độ dài của hai cạnh bên 

Ví dụ: Với hình thang ABCD (AB//CD) có AB = 4 cm, CD = 8 cm, BC = 5 cm, AD vuông góc với DC và AD = 3 cm. Tính chu vi của hình thang ABCD.

Hướng dẫn: Chu vi của hình thang ABCD được tính là: 8 + 4 + 5 + 3 = 20 (cm)

4. Các dạng bài tập thường gặp về hình thang vuông

Chủ đề 1: Tính số đo góc

Cách giải: Dựa vào đặc điểm tổng của bốn góc trong một tứ giác và hai đường thẳng song song cùng với kiến thức về hình thang vuông, chúng ta sẽ xác định chính xác số đo các góc.

Ví dụ 1: Trong hình thang ABCD với AB song song CD, góc A bằng ba lần góc D. Góc B lớn hơn góc C 30 độ. Xác định số đo các góc của hình thang.

Ví dụ 2: Trong hình thang vuông ABCD với AB song song CD, biết rằng góc A gấp đôi góc D, tìm số đo các góc của hình thang.

Chủ đề 2: Chứng minh hình thang vuông

Cách giải: Áp dụng định nghĩa của hình thang vuông để chứng minh hình theo yêu cầu.

Ví dụ 1: Cho tam giác ABC vuông cân tại A. Vẽ tam giác ACD vuông cân tại D nằm ngoài tam giác ABC. Tứ giác ABCD là hình gì? Giải thích tại sao?

Ví dụ 2: Trong tam giác ABC vuông tại A, với BD và CE là hai đường trung tuyến. Chứng minh rằng BCDE là hình thang vuông.

Chủ đề 3: Sử dụng các tính chất của hình thang vuông để giải quyết bài toán 

Cách giải: Dựa vào các tính chất về cạnh và góc của hình thang vuông đã học để giải quyết bài toán.

Ví dụ 1: Trong hình thang vuông ABCD, góc A và góc D đều bằng 90 độ, AB = AD, DC = 2AB và BE vuông góc với CD tại điểm E.

a, Chứng minh rằng tam giác ABD đồng dạng với tam giác EDB

b, Chứng minh rằng tam giác BEC là tam giác vuông cân tại E

Ví dụ 2: Trong tam giác vuông cân ABCD tại A, vẽ tam giác ACD vuông cân tại D ngoài tam giác ABC. Tứ giác ABCD là hình gì? Giải thích lý do.

Hướng dẫn giải: Chứng minh tam giác ABC là tam giác vuông cân tại A => Chứng minh tam giác ADC là tam giác vuông cân tại D => Góc DAC và góc ACB là hai góc so le trong => AD song song với BC, do đó tứ giác ABCD có AD song song với BC và góc ADC bằng 90 độ. Kết luận rằng ABCD là hình thang vuông.

Hình thang vuông là một dạng đặc biệt của hình thang, vì vậy nó cũng mang những đặc điểm và tính chất tương tự như hình thang. Để giải các bài tập liên quan đến hình thang vuông, chúng ta cần nắm vững các kiến thức cơ bản về khái niệm, tính chất, dấu hiệu nhận biết và các đặc điểm của nó.

BÀI TẬP LUYỆN TẬP

Câu 1. Một hình thang cân có đường chéo vuông góc với cạnh bên. Đáy nhỏ dài 14 cm, đáy lớn dài 50 cm. Tính diện tích của hình thang.

Câu 2: Mảnh đất hình thang có đáy lớn dài 38 m và đáy nhỏ dài 28 m. Nếu mở rộng hai đáy sang bên phải, đáy lớn thêm 9 m và đáy nhỏ thêm 8 m, sẽ thu được mảnh đất hình thang mới có diện tích lớn hơn diện tích mảnh đất ban đầu là 107,2 m². Tính diện tích của mảnh đất hình thang ban đầu.

Câu 3. Trong tam giác vuông cân ABC tại A, vẽ tam giác ACD vuông cân tại D bên ngoài tam giác ABC. Tứ giác ABCD là hình gì? Giải thích lý do.

Câu 4. Trong hình thang vuông ABCD, có AD = 6 cm; DC = 12 cm; và AB = 2/3 DC

a, Tính diện tích của hình thang ABCD

b, Nếu kéo dài các cạnh bên AD và CB cho đến khi chúng cắt nhau tại điểm M, hãy tính độ dài của cạnh AM.

Câu 5: Chứng minh rằng trong một hình thang vuông, hiệu của bình phương các đường chéo bằng hiệu của bình phương các đáy.

Câu 6: Trong tam giác vuông ABC tại A, vẽ đường cao AH. Từ H, vẽ HD vuông góc với AC và HE vuông góc với AB. Gọi M và N lần lượt là trung điểm của các đoạn HB và HC. Chứng minh rằng tứ giác DEMN là hình thang vuông.

Câu 7: Trong hình thang ABCD vuông tại A và D, biết rằng AD = 20 cm, AC = 52 cm, và BC = 29 cm. Tính độ dài của AB.

Câu 8: Trong hình thang ABCD vuông tại A và D, gọi M là trung điểm của AD. Biết rằng MB vuông góc với MC.

a, Chứng minh rằng BC = AB + CD;

b, Vẽ MH vuông góc với BC. Chứng minh rằng tứ giác MBHD là hình thang.

Câu 9: Trong tam giác vuông ABC tại A, chọn điểm M trên cạnh BC sao cho AM = 1/2 BC, và N là trung điểm của cạnh AB. Chứng minh rằng:

a, Tam giác AMB là tam giác cân

b, Tứ giác MNAC là hình thang vuông

Đáp án:

Câu 1. 30 cm²

Câu 2. Diện tích của mảnh đất ban đầu là 415,8 m²

^{Câu 3. Giải pháp: ABCD là hình thang vuông.}

^{Câu 4:} 

a, 60 cm²

b. Độ dài AM là 12 cm

Câu 9: 

a, Hướng dẫn giải: Chứng minh M là trung điểm của cạnh BC, từ đó AM = AB = MC = BC/2. Do đó, tam giác AMB là tam giác cân.

b, Hướng dẫn giải: Trong tam giác AMB, AN = NB (theo giả thiết)

Vì vậy: MN vuông góc với AB; AC cũng vuông góc với AB, do đó MN song song với AC và góc CAN bằng 90^o.

Từ đó, tứ giác MNAC là hình thang vuông.

Đây là bài viết của Mytour trả lời cho câu hỏi Hình thang là gì? Dấu hiệu nhận biết, tính chất của hình thang, hy vọng với những kiến thức về hình thang vuông trên có thể giúp bạn củng cố kiến thức của mình.