Hình tròn

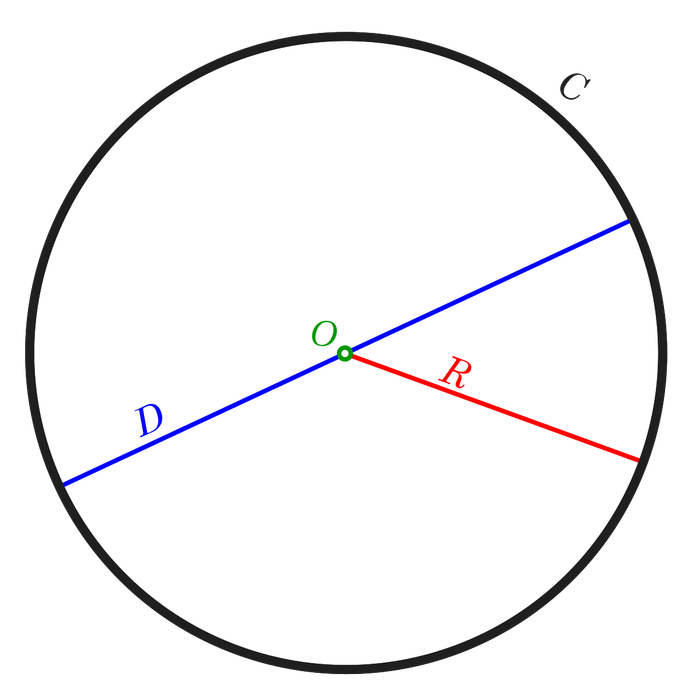
Trong hình học, một hình tròn là một vùng trong mặt phẳng giới hạn bởi một vòng tròn. Một hình tròn được coi là đóng nếu nó bao quanh đường tròn tạo thành biên của nó và mở nếu không.

Công thức

Trong hệ tọa độ Descartes, hình tròn mở có tâm $(a,b)$ và bán kính R được biểu diễn theo công thức

Trong hình học, điểm D là tập hợp các điểm (x, y) trong mặt phẳng Euclid sao cho khoảng cách từ điểm này đến điểm (a, b) nhỏ hơn bán kính R.

Hình tròn đóng là hình có tâm và bán kính nhất định.

Điểm D với dấu gạch ngang trên (D¯) là tập hợp các điểm (x, y) trong mặt phẳng Euclid sao cho khoảng cách từ điểm này đến điểm (a, b) không vượt quá bán kính R.

Diện tích của một hình tròn là πR² (xem diện tích hình tròn để biết thêm chi tiết).

Một số tính chất liên quan đến hình tròn.

Hình tròn có đặc tính đối xứng hoàn toàn.

Hình tròn mở và hình tròn đóng không tương đương về định tính (không đồng phôi), vì chúng có các thuộc tính topo khác nhau. Ví dụ, mọi hình tròn đóng đều nén trong khi mọi hình tròn mở không nén. Tuy nhiên, từ góc độ topo đại số, chúng có nhiều đặc điểm chung: cả hai đều có thể co lại và do đó, tương đồng với một điểm duy nhất. Điều này ngụ ý rằng các nhóm cơ bản của chúng không quan trọng, và tất cả các nhóm tương đồng không quan trọng ngoại trừ nhóm thứ 0, cũng là đẳng cấu của Z. Đặc điểm Euler của một điểm (và do đó cũng của một hình tròn đóng hoặc mở) là 1.

Mọi ánh xạ liên tục từ hình tròn đóng đến chính nó đều có ít nhất một điểm bất động (không yêu cầu ánh xạ là song ánh hoặc toàn ánh); đây là trường hợp n = 2 của định lý điểm bất động Brouwer. Tuyên bố này không đúng với hình tròn mở:

Xem ví dụ về hàm $f(x,y)=\left(\frac{x+\sqrt{1-<!--\; -\; -->y^2}}{2},y\right)$ ánh xạ từ mọi điểm trên hình tròn đơn vị mở sang một điểm khác trên bề mặt hình tròn đơn vị mở nằm bên phải của điểm đã cho. Nhưng với hình tròn đơn vị đóng, nó ánh xạ mọi điểm trên nửa vòng tròn $x^2+y^2=1,x>0.$

• Cầu
• Đường tròn có đường kính từ trung tâm đến trọng tâm