Nhằm hỗ trợ học sinh lớp 8 trong việc học tập, Mytour giới thiệu Chuyên đề Hình vuông.
Tài liệu này cung cấp tổng quan về kiến thức lý thuyết như định nghĩa, tính chất, dấu hiệu nhận biết và các bài tập về hình vuông trong môn Toán lớp 8. Ngoài ra, bạn cũng có thể tham khảo chuyên đề Hình thoi. Dưới đây là nội dung chi tiết, mời bạn tham khảo và tải tài liệu tại đây.
I. Lý thuyết về hình vuông
1. Định nghĩa
Hình vuông là một tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
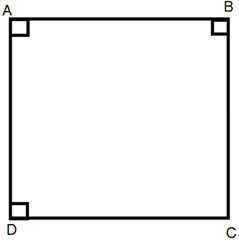

Chú ý:
+ Hình vuông là một dạng đặc biệt của hình chữ nhật với bốn cạnh bằng nhau.
+ Hình vuông cũng là một dạng đặc biệt của hình thoi với bốn góc vuông.
+ Hình vuông đồng thời là hình chữ nhật và hình thoi.
2. Tính chất
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
3. Dấu hiệu nhận biết hình vuông
+ Nếu hai cạnh kề của hình chữ nhật bằng nhau, đó là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
Ví dụ: Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.
II. Bài tập tự luyện
Bài 1: Cho hình chữ nhật ABCD có AB = 2AD. Gọi P, Q lần lượt là trung điểm của AB, CD.
a. Chứng minh tứ giác APQD và PBCQ là hình vuông
b. Gọi H là giao điểm của AQ và DP. Gọi K là giao điểm của CP và BQ. Chứng minh PHQK là hình vuông
Bài 2: Cho hình chữ nhật MNRS có MN = 2MS. Gọi P, Q lần lượt là trung điểm của MN;SR.
a. Chứng minh tứ giác MPQS và PNRQ là hình vuông
b. Gọi H là giao điểm của MQ và SP. Gọi K là giao điểm của RP và NQ. Chứng minh PHQK là hình vuông
Bài 3: Cho hình chữ nhật ABCD có AB = 10cm và AD = 5cm. Gọi P, Q lần lượt là trung điểm của AB, CD.
a. Chứng minh tứ giác APQD và PBCQ là hình vuông
b. Gọi H là giao điểm của AQ và DP. Gọi K là giao điểm của CP và BQ. Chứng minh PHQK là hình vuông
Bài 4: Cho tam giác ABC vuông tại A. Đường phân giác AD. Gọi M, N theo thứ tự là chân đường vuông góc hạ từ D đến AB, AC.
a. Chứng minh AMDN là hình vuông
b. Gọi P đối xứng với D qua M. Chứng minh ADBP là hình thoi
c. NMPA là hình bình hành
Bài 5: Cho tam giác EFK vuông tại E. Đường phân giác ED. Gọi M, N theo thứ tự là chân đường vuông góc hạ từ D đến EF, EK.
a. Chứng minh EMDN là hình vuông
b. Gọi P đối xứng với D qua M. Chứng minh EDFP là hình thoi
c. NMPE là hình bình hành
Bài 6: Cho tam giác ABC vuông tại A. Đường phân giác AD. Gọi M, N theo thứ tự là chân đường vuông góc hạ từ D đến AB, AC.
d. Chứng minh AMDN là hình vuông
e. Gọi P đối xứng với D qua M. Tính độ dài DP biết AC = 10cm
f. NMPA là hình bình hành
Bài 7: Cho hình thang vuông ABCD có góc A bằng góc D và cùng bằng 90. AB = 3cm, AD = 8cm. CD = 5cm. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi K là hình chiếu của M trên CD. Chứng minh MNDK là hình vuông
Bài 8: Cho hình thang vuông ABCD có góc A bằng góc D và cùng bằng 90. AB = 6cm, AD = 16cm. CD = 10cm. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi K là hình chiếu của M trên CD. Chứng minh MNDK là hình vuông
Bài 9: Cho hình vuông ABCD. Lấy các điểm E, F theo thứ tự thuộc các cạnh CD, DA, sao cho AF = DE. Chứng minh AE = BF. Và AE vuông góc BF
Bài 10: Cho hình vuông ABCD. Lấy các điểm E, F theo thứ tự là trung điểm của các cạnh CD, DA. Chứng minh AE = BF. Và AE vuông góc BF
Bài 11: Cho hình vuông ABCD. Lấy các điểm của M, N, P, Q theo thứ tự thuộc các cạnh AB, BC, CD, DA sao cho AM = BN = CP = DQ Tứ giác MNPQ là hình gì? Vì sao ?
Bài 12: Cho tam giác ABC. Điểm M thuộc BC. Qua M dựng đường thẳng song song với AB cắt AC tại D, Qua M dựng đường thẳng song song với AC cắt AB tại E
a. Tứ giác ADME là hình gì ? Vì sao
b. Tìm điều kiện của tam giác ABC để tứ giác ADME là hình chữ nhật
Bài 13: Trong tam giác ABC vuông tại A, M thuộc BC. Dựng đường thẳng MD // AB, cắt AC tại D và đường thẳng ME // AC, cắt AB tại E
c. Tứ giác ADME là hình gì ? Tại sao ?
d. Điều kiện để tam giác ABC là hình vuông ADME
Bài 14: Trong hình vuông tại A, AM là trung tuyến. I là trung điểm của AB, N là điểm đối xứng với M qua I
a. Tính chất của các tứ giác ANMC, AMBN ? Tại sao ?
b. Với AB = 4cm và AC = 6cm, tính diện tích tứ giác AMBN
c. Điều kiện cần của tam giác vuông ABC để AMBN là hình vuông
Bài 15: Cho tứ giác ABCD, M, N, P, Q lần lượt là trung điểm của AB, BC, CD và DA.
a. Chứng minh MNPQ là hình bình hành.
b. Điều kiện cho hai đường chéo AC và BD của tứ giác để MNPQ là hình chữ nhật, hình thoi, hình vuông
Bài 16: Cho tam giác ABC vuông tại A, AB = 5cm, AC = 12cm, AM là trung tuyến.
a. Tính độ dài BC, AM.
b. Trên tia AM lấy điểm D đối xứng với A qua M. Chứng minh AD = BC. Điều kiện cần của tam giác vuông ABC để ABDC là hình vuông
Bài 17: Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Gọi AM là trung tuyến của tam giác.
a) Tính độ dài AM.
b) Kẻ MD vuông góc với AB, ME vuông góc với AC. Tứ giác ADME có dạng đặc biệt nào ?
c) Tứ giác DECB có dạng đặc biệt nào ?
Bài 18: Cho tam giác ABC vuông ở A, đường cao AH.
1. Chứng minh AH. BC = AB. AC.
2. Gọi M là điểm nằm giữa B và C. Kẻ MN AB, MP AC ( N AB, P AC).
Tứ giác ANMP có thuộc tính gì? Vì sao?
3. Tính góc NHP.
4. Xác định vị trí của điểm M trên BC để NP có chiều dài nhỏ nhất.
