Hướng dẫn cách tính bán kính của đường tròn ngoại tiếp tam giác một cách đơn giản và dễ hiểu

Buzz

Nội dung bài viết

1. Định nghĩa đường tròn ngoại tiếp tam giác

2. Các tính chất của đường tròn ngoại tiếp tam giác

3. Công thức tính bán kính đường tròn ngoại tiếp

4. Bài tập thực hành

5. Một số bài tập để luyện tập

Xem thêm

Dưới đây là hướng dẫn về cách tính bán kính của đường tròn ngoại tiếp tam giác một cách dễ nắm bắt

1. Định nghĩa đường tròn ngoại tiếp tam giác

Đường tròn ngoại tiếp tam giác là đường tròn tiếp xúc với bên ngoài của tam giác. Cụ thể, đường tròn này đi qua tất cả ba đỉnh của tam giác. Tâm của đường tròn ngoại tiếp được xác định là giao điểm của ba đường trung trực của tam giác đó. Đường tròn ngoại tiếp còn được gọi là đường tròn nội tiếp tam giác (hoặc tam giác nằm trong đường tròn).

Hướng dẫn tính bán kính đường tròn ngoại tiếp tam giác một cách đơn giản và dễ hiểu

Khi kết nối tâm O của đường tròn với ba đỉnh của tam giác ABC, chúng ta nhận được ba đoạn thẳng OA, OB và OC. Độ dài của các đoạn thẳng này đều bằng nhau và chính là bán kính của đường tròn ngoại tiếp tam giác ABC mà chúng ta cần xác định.

2. Các tính chất của đường tròn ngoại tiếp tam giác

Đường tròn ngoại tiếp tam giác có những đặc điểm quan trọng mà học sinh cần ghi nhớ như sau:

- Mỗi tam giác chỉ có một đường tròn ngoại tiếp duy nhất.

- Tâm của đường tròn ngoại tiếp chính là điểm giao nhau của ba đường trung trực của tam giác.

- Trong tam giác vuông, điểm giữa của cạnh huyền chính là tâm của đường tròn ngoại tiếp tam giác đó.

- Đối với tam giác đều, cả tâm của đường tròn ngoại tiếp và nội tiếp đều là cùng một điểm.

3. Công thức tính bán kính đường tròn ngoại tiếp

Đây là loại bài tập thường gặp trong các kỳ thi. Vì vậy, học sinh nên nắm vững cách giải để có thể làm bài một cách hiệu quả.

Cho tam giác ABC với các cạnh AB = c, AC = b, BC = a. R là bán kính của đường tròn ngoại tiếp tam giác và S là diện tích của tam giác ABC.

Phương pháp 1: Áp dụng công thức diện tích của tam giác

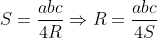
$S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S}$

Phương pháp 2: Sử dụng định lý Sin trong tam giác

Chúng ta có:

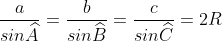
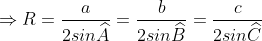
$\frac{a}{\sin\widehat{A}} = \frac{b}{\sin\widehat{B}} = \frac{c}{\sin\widehat{C}} = 2R$ $\Rightarrow R = \frac{a}{2\sin\widehat{A}} = \frac{b}{2\sin\widehat{B}} = \frac{c}{2\sin\widehat{C}}$

Phương pháp 3: Đặc điểm của tam giác vuông

Tâm của đường tròn ngoại tiếp trong một tam giác vuông chính là trung điểm của cạnh huyền. Do đó, bán kính của đường tròn ngoại tiếp tam giác vuông bằng nửa chiều dài của cạnh huyền.

Phương pháp 4: Áp dụng hệ tọa độ

- Xác định tọa độ của tâm O của đường tròn ngoại tiếp tam giác ABC

- Xác định tọa độ của một trong ba đỉnh A, B, C (nếu chưa có thông tin)

- Tính khoảng cách từ tâm O đến một trong ba đỉnh A, B, C; đây chính là bán kính cần tìm: R = OA = OB = OC

* Phương pháp tính bán kính đường tròn ngoại tiếp tam giác đều

Tam giác đều là loại tam giác có ba cạnh và ba góc đều bằng nhau. Bán kính của đường tròn ngoại tiếp tam giác đều bằng chính độ dài của một cạnh của tam giác đó.

Vì các cạnh của tam giác đều đều bằng nhau, bạn có thể áp dụng công thức sau để tính bán kính của đường tròn ngoại tiếp tam giác đều:

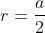
$r = \frac{a}{2}$

Công thức này được mô tả như sau:

+ r là bán kính của đường tròn ngoại tiếp tam giác đều

+ a là độ dài của mỗi cạnh của tam giác đều

Lưu ý rằng công thức này chỉ áp dụng cho tam giác đều. Đối với các loại tam giác khác, hãy sử dụng công thức tính bán kính đường tròn ngoại tiếp đã được trình bày trước đó.

4. Bài tập thực hành

Bài 1: Xét tam giác ABC với AB = 3, AC = 5 và BC = 6. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn giải

Sử dụng công thức Heron để tính diện tích của tam giác ABC như sau:

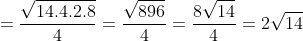
$S = \frac{\sqrt{(AB + AC + BC)(AB + BC - AC)(AB + AC - BC)(BC + AC - AB)}}{4}$ $= \frac{\sqrt{(3+5+6)(3+6-5)(3+5-6)(6+5-3)}}{4}$ $= \frac{\sqrt{14\cdot4\cdot2\cdot8}}{4}= \frac{\sqrt{896}}{4}= \frac{8\sqrt{14}}{4}= 2\sqrt{14}$

Bán kính của đường tròn ngoại tiếp tam giác ABC được tính như sau

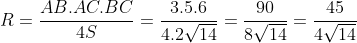$R= \frac{AB\cdot AC\cdot BC}{4S}= \frac{3\cdot5\cdot6}{4\cdot2\sqrt{14}}= \frac{90}{8\sqrt{14}}= \frac{45}{4\sqrt{14}}$ Bài 2: $\widehat{A} = \widehat{B} = 90^{\circ}$

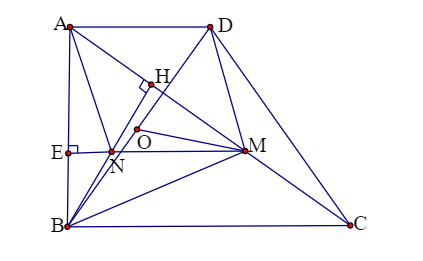
Phương pháp tính bán kính đường tròn ngoại tiếp tam giác một cách đơn giản và dễ hiểu

Ký hiệu N là điểm giữa của BH, do đó MN là đoạn trung bình của tam giác HBC, dẫn đến MN ⊥ AB

Ngoài ra, BH ⊥ AM

=> N là trực tâm của tam giác ABM

=> AN ⊥ BM

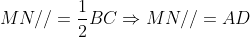
$MN // = \frac{1}{2} BC, vì vậy MN // AD$

Do đó, ADMN là hình bình hành, dẫn đến AN // DM

Từ đó suy ra: DM ⊥ MB và tam giác DBM vuông tại M, vì vậy tâm đường tròn ngoại tiếp tam giác DBM là trung điểm O của BD

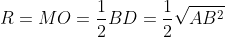
$R = MO = \frac{1}{2} BD = \frac{1}{2} \sqrt{AB^{2} + AD^{2}} = \frac{1}{2} \sqrt{4a^{2} + a^{2}} = \frac{a\sqrt{5}}{2}$

Bài 3: Xét tam giác ABC với góc B là 45° và AC = 4. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn giải:

Gọi R là bán kính của đường tròn ngoại tiếp tam giác ABC.

Chúng ta có: b = AC = 4

Sử dụng định lý sin cho tam giác ABC, ta có:

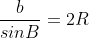
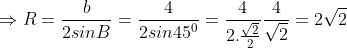
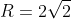
$\frac{b}{\sin B} = 2R$ $Do đó, R = \frac{b}{2\sin B} = \frac{4}{2\sin 45^{0}} = \frac{4}{2 \times \frac{\sqrt{2}}{2}} = \frac{4}{\sqrt{2}} = 2\sqrt{2}$ $R = 2\sqrt{2}$

Bài 4: Xét tam giác MNP với MN = 6, MP = 8 và PN = 10. Tính bán kính của đường tròn ngoại tiếp tam giác MNP.

Hướng dẫn giải:

Có: MN² = 6² = 36; MP² = 8² = 64;

PN² = 10² = 100

Ta có 36 + 64 = 100

Do đó, MN² + MP² = PN²

Vậy tam giác MNP là tam giác vuông tại M (theo định lý Pytago)

Bán kính của đường tròn ngoại tiếp tam giác MNP được tính như sau:

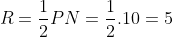
$R = \frac{1}{2} PN = \frac{1}{2} \times 10 = 5$

Bài 5: Xét tam giác ABC với BC = 10. Đường tròn (I) có tâm I nằm trên cạnh BC và tiếp xúc với các cạnh AB, AC tại M và N tương ứng. Biết rằng bán kính của (I) là 3 và 2IB = 3IC. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn giải:

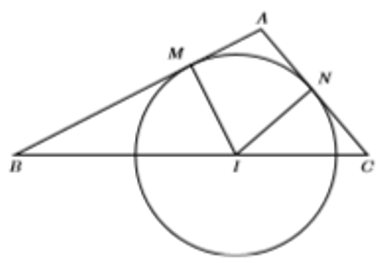
Cách tính bán kính của đường tròn ngoại tiếp tam giác một cách đơn giản và dễ hiểu.

+ Do 2IB = 3IC

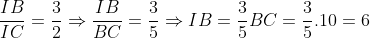
$\frac{IB}{IC} = \frac{3}{2} \Rightarrow \frac{IB}{BC} = \frac{3}{5} \Rightarrow IB = \frac{3}{5} BC = \frac{3}{5} \times 10 = 6$

IC = BC - IB = 10 - 6 = 4

+ M và N là các điểm tiếp xúc của đường tròn tâm I với các cạnh AB và AC

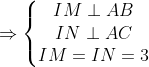
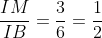
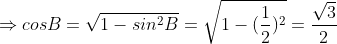
$\Rightarrow \left\{\begin{matrix} IM \perp AB & & \\ IN \perp AC & & \\ IM = IN = 3 & & \end{matrix}\right.$ $\frac{IM}{IB} = \frac{3}{6} = \frac{1}{2}$ $\Rightarrow \cos B = \sqrt{1 - \sin^{2} B} = \sqrt{1 - (\frac{1}{2})^{2}} = \frac{\sqrt{3}}{2}$

(vì góc B là góc nhọn)

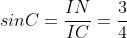
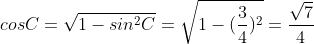
$\sin C = \frac{IN}{IC} = \frac{3}{4}$ $\cos C = \sqrt{1 - \sin^{2} C} = \sqrt{1 - (\frac{3}{4})^{2}} = \frac{\sqrt{7}}{4}$

(vì góc C là góc nhọn)

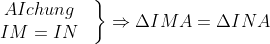
$\left\{\begin{matrix} AI chung & \\ IM = IN & \end{matrix}\right.\Rightarrow \Delta IMA = \Delta INA$

(cạnh huyền trong tam giác vuông)

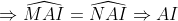
$\Rightarrow \widehat{MAI} = \widehat{NAI} \Rightarrow AI$

Gọi AB = c, AC = b

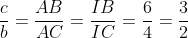
$\frac{c}{b} = \frac{AB}{AC} = \frac{IB}{IC} = \frac{6}{4} = \frac{3}{2}$

\Rightarrow 2c = 3b

+ Theo định lý Cô-sin trong tam giác ABC, ta có:

c^{2} = b^{2} + BC^{2} - 2b \cdot BC \cdot \cos C

Thay số vào ta có hệ phương trình sau:

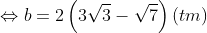
$\left\{\begin{matrix} 2c = 3b & \\ c^{2} = b^{2} + 100 - 2b \cdot 10 \cdot \frac{\sqrt{7}}{4} & \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} c = \frac{3}{2}b & \\ \left( \frac{3}{2}b \right)^{2} = b^{2} - 5 \sqrt{7}b + 100 & \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} c = \frac{3}{2}b & \\ \frac{5}{4}b^{2} - 5 \sqrt{7}b + 100 = 0 & \end{matrix}\right.$ $\Leftrightarrow b = 2\left( 3 \sqrt{3} - \sqrt{7} \right) \text{ (thực nghiệm)}$ $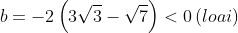b = -2\left( 3 \sqrt{3} - \sqrt{7} \right) < 0 \text{ (loại)}$ $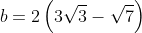b = 2\left( 3\sqrt{3} - \sqrt{7} \right)$

Áp dụng định lý sin trong tam giác ABC, ta có:

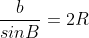
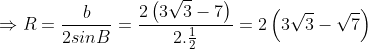
$\frac{b}{\sin B} = 2R$ $\Rightarrow R = \frac{b}{2 \sin B} = \frac{2\left( 3\sqrt{3} - \sqrt{7} \right)}{2 \cdot \frac{1}{2}} = 2\left( 3\sqrt{3} - \sqrt{7} \right)$

Như vậy, bán kính đường tròn ngoại tiếp tam giác ABC là:

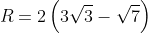
$R = 2\left( 3\sqrt{3} - \sqrt{7} \right)$

Bài 6: Trong tam giác vuông ABC với góc vuông tại A, có AB = 1 và AC = 4. Gọi M là điểm giữa của AC

a) Tính diện tích của tam giác ABC

b) Tính bán kính R₁ của đường tròn ngoại tiếp tam giác ABC

c) Tính bán kính R₂ của đường tròn ngoại tiếp tam giác CBM

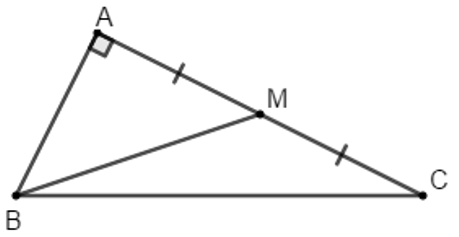
Phương pháp tính bán kính đường tròn ngoại tiếp tam giác đơn giản và dễ hiểu

Hướng dẫn giải:

a) Tam giác ABC vuông tại A, do đó diện tích của tam giác ABC được tính như sau:

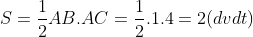
$S = \frac{1}{2} \times AB \times AC = \frac{1}{2} \times 1 \times 4 = 2 (đvdt)$

b) Với tam giác ABC vuông tại A, áp dụng định lý Pytago ta có:

BC² = AB² + AC² = 1² + 4² = 17

$Do đó, BC = \sqrt{17}$

Bán kính của đường tròn ngoại tiếp tam giác ABC được tính như sau:

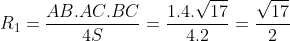
$R_{1} = \frac{AB \times AC \times BC}{4S} = \frac{1 \times 4 \times \sqrt{17}}{4 \times 2} = \frac{\sqrt{17}}{2}$

c) M là trung điểm của AC, do đó:

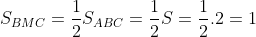
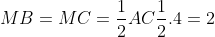
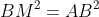
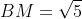
$Diện tích của tam giác BMC là: \frac{1}{2} diện tích tam giác ABC = \frac{1}{2} \times 2 = 1$ $MB = MC = \frac{1}{2} AC = \frac{1}{2} \times 4 = 2$ $BM^{2} = AB^{2} + AM^{2} = 1^{2} + 2^{2} = 5$ $BM = \sqrt{5}$

Bán kính của đường tròn ngoại tiếp tam giác CMB là:

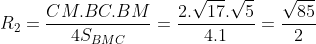
$Bán kính của đường tròn ngoại tiếp tam giác CMB là: \frac{CM \cdot BC \cdot BM}{4 \cdot S_{BMC}} = \frac{2 \cdot \sqrt{17} \cdot \sqrt{5}}{4 \cdot 1} = \frac{\sqrt{85}}{2}$

5. Một số bài tập để luyện tập

Chúng tôi sẽ cung cấp cho các em học sinh một số bài tập toán về đường tròn ngoại tiếp tam giác, giúp các em nắm vững kiến thức và hoàn thành các bài tập hiệu quả nhất.

Bài 1: Xét tam giác ABC với tọa độ A (1; 3), B (-1; 1), C (2; 2). Tìm tọa độ của tâm đường tròn ngoại tiếp tam giác ABC.

Bài 2: Xét tam giác ABC vuông tại A với AB = 6 cm và BC = 8 cm. Xác định tâm và bán kính của đường tròn ngoại tiếp tam giác ABC. Bán kính đường tròn ngoại tiếp là bao nhiêu?

Bài 3: Cho tam giác CBH với ba góc nhọn nằm trong một đường tròn (O; R). Ba đường chéo MF, NE, và PD của tam giác cắt nhau tại H. Chứng minh rằng tứ giác NDEP là tứ giác nội tiếp.

Bài 4: Xét tam giác ABC đều với mỗi cạnh dài 8 cm. Tìm bán kính và tâm của đường tròn ngoại tiếp tam giác ABC.

Bài 5: Xét tam giác ABC đều với các cạnh dài 8 cm. Xác định bán kính và tâm của đường tròn ngoại tiếp tam giác này.

Bài 6: Viết phương trình của đường tròn nội tiếp tam giác ABC với các tọa độ đỉnh đã cho là A(-1;3), B(5;1), và C(-1;3).

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]

Các câu hỏi thường gặp

Đường tròn ngoại tiếp tam giác là gì và có đặc điểm gì nổi bật?

Đường tròn ngoại tiếp tam giác là đường tròn tiếp xúc bên ngoài của tam giác, đi qua tất cả ba đỉnh của nó. Một số đặc điểm nổi bật bao gồm chỉ có một đường tròn ngoại tiếp duy nhất cho mỗi tam giác, tâm của nó là giao điểm của ba đường trung trực, và trong tam giác vuông, tâm nằm giữa cạnh huyền.

Làm thế nào để tính bán kính của đường tròn ngoại tiếp tam giác?

Để tính bán kính của đường tròn ngoại tiếp tam giác, bạn có thể sử dụng công thức R = abc / 4S, trong đó a, b, c là độ dài các cạnh, và S là diện tích tam giác. Có thể áp dụng định lý Sin hoặc phương pháp Heron tùy thuộc vào loại tam giác.

Có bao nhiêu phương pháp để tính bán kính đường tròn ngoại tiếp tam giác?

Có nhiều phương pháp để tính bán kính đường tròn ngoại tiếp tam giác, bao gồm sử dụng công thức Heron, định lý Sin, và đặc điểm của tam giác vuông. Tùy vào dữ liệu đầu vào, mỗi phương pháp có thể được áp dụng linh hoạt để đạt kết quả chính xác.

Tâm của đường tròn ngoại tiếp tam giác nằm ở đâu trong tam giác vuông?

Tâm của đường tròn ngoại tiếp tam giác vuông nằm tại trung điểm của cạnh huyền. Điều này có nghĩa là bán kính của đường tròn ngoại tiếp sẽ bằng nửa chiều dài của cạnh huyền trong tam giác vuông.