Hướng dẫn cách tính độ dài của Vecto một cách đơn giản và chính xác nhất dành cho lớp 10

Buzz

Nội dung bài viết

1. Phương pháp tính độ dài của vecto một cách đơn giản và chính xác

2. Ví dụ minh họa cho bài toán trên

3. Bài tập luyện tập

Xem thêm

Bài viết này từ Mytour sẽ cung cấp cho bạn đọc một cái nhìn chi tiết về cách tính độ dài Vecto một cách đơn giản và chính xác nhất cho môn Toán lớp 10. Xin mời các bạn theo dõi để hiểu rõ hơn về chủ đề này.

1. Phương pháp tính độ dài của vecto một cách đơn giản và chính xác

Chiều dài của vecto:

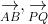
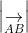
$\left | \underset{a}{\rightarrow} \right |$ $\underset{AB }{\rightarrow}, \underset{PQ}{\rightarrow}$ $\left | \underset{AB}{\rightarrow} \right |$ $\left | \underset{PQ}{\rightarrow} \right |$

- Cách thực hiện: Để xác định độ dài của vecto, ta tính khoảng cách giữa điểm đầu và điểm cuối của vecto:

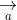
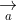
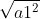
$\underset{a }{\rightarrow}$ $\underset{a}{\rightarrow}$ $\left | \underset{a}{\rightarrow} \right |$ $\sqrt{a1^{2} + a2^{2}}$

Khoảng cách giữa hai điểm trong hệ tọa độ:

Áp dụng công thức:

Trong hệ tọa độ phẳng, khoảng cách giữa hai điểm M (xM; yM) và N (xN; yN) được tính bằng:

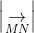
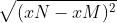
$\left | \underset{MN}{\rightarrow} \right |$ $\sqrt{(xN - xM)^{2} + (yN - yM)^{2}}$

2. Ví dụ minh họa cho bài toán trên

Câu 1: Tính khoảng cách giữa hai điểm M (1; -2) và N (-3; 4) trong hệ tọa độ Oxy

Hướng dẫn cách giải bài toán:

Sử dụng công thức để tính khoảng cách giữa hai điểm:

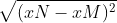
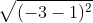
$\sqrt{(xN - xM)^{2} + (yN - yM)^{2}}$ $\sqrt{(-3 - 1)^{2} + (4 - (-2))^{2}}$

= căn của 52 = 2 căn của 13

Câu 2: Trong hệ toạ độ Oxy, có bốn điểm A (-1; 1); B (0; 2); C (3; 1) và D (0; -2). Khẳng định nào dưới đây là chính xác?

A. Tứ giác ABCD là hình bình hành

B. Tứ giác ABCD là hình thoi

C. Tứ giác ABCD là hình thang cân

D. Tứ giác ABCD không thể nội tiếp một đường tròn

Hướng dẫn cách giải:

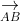
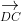
$\underset{AB}{\rightarrow}$ $\underset{DC}{\rightarrow}$

Kết luận: vecto DC bằng 3 lần vecto AB

Kết luận: DC song song với AB

Vì vậy, tứ giác ABCD là hình thang (1)

Cùng với đó:

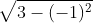$\sqrt{(3 - (-1))^{2} + (1 - 1)^{2}}$ ² $\sqrt{(0 - 0)^{2} + (-2 - 2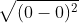)^{2}}$ ²

Do đó, có thể kết luận: AC = BD (2)

Từ (1) và (2) suy ra, tứ giác ABCD là hình thang cân (hình thang có hai đường chéo bằng nhau là hình thang cân)

Đáp án chính xác là đáp án C

Câu 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với các điểm A(1 ; 4), B(3 ; 2), và C(5 ; 4). Hãy tính chu vi của tam giác này.

A. P = 4 + 2√2

B. P = 4 + 4√2

C. P = 8 + 8√2

D. P = 2 + 2√2

Hướng dẫn giải:

Chúng ta có:

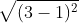
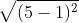
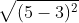
$\sqrt{(3 -1)^{2}+ (2 -4)^{2})}$ $\sqrt{(5 -1)^{2}+ (4 -4)^{2})}$ $\sqrt{(5 -3)^{2}+ (4 - 2)^{2})}$

Chu vi của tam giác ABC được tính như sau:

P = AB + AC + BC = 2√2 + 4 + 2√2 = 4 + 4√2

Do đó, đáp án chính xác là đáp án B

Câu 4: Trong mặt phẳng tọa độ Oxy với hai điểm A (1 ;3) và B (4 ;2). Tìm tọa độ điểm C trên trục hoành sao cho C cách đều hai điểm A và B

A. C (-5/3 ; 0)

B. C (5/3 ; 0)

C. (-3/5 ; 0)

D. (3/5 ; 0)

Hướng dẫn giải quyết:

Vì C nằm trên trục Ox nên tọa độ của C là (x; 0)

Vì vậy ta có:

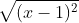
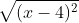
$sqrt{(x - 1)^{2} + (-3)^{2}}$ $sqrt{(x - 4)^{2} + (-2)^{2}}$

Vì điểm C cách đều hai điểm A và B, ta có:

CA = CB

Do đó, AC^{2} = BC^{2}

^{CA = CB tương đương với AC^{2} = BC^{2}}

Tương đương: (x - 1)^{2} + (-3)^{2} = (x - 4)^{2} + (-2)^{2}

Tương đương: x^{2} - 2x + 1 + 9 = x^{2} - 8x + 16 + 4

Tương đương: (x^{2} - x^{2}) + (-2x + 8x) = 16 + 4 - 1 - 9

Tương đương: 6x = 10

Tương đương với x = 10/6

Tương đương với x = 5/3

Vậy tọa độ của C là (5/3 ; 0)

3. Bài tập luyện tập

Câu 1: Trong mặt phẳng tọa độ Ôxy, cho hai vectơ v = (4 ; 1) và u = (1 ; 4). Tính độ dài của vectơ u + v và vectơ u + v

Câu 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm M (1; -2) và N (-3; 4). Hãy tính khoảng cách giữa hai điểm này

A. MN = 4

B. MN = 6

C. MN = 3√6

D. MN = 2√13

Câu 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với các đỉnh A (1; 4), B (3; 2) và C (5; 4). Tính chu vi của tam giác này

A. P = 4 + 2√2

B. P = 4 + 4√2

C. P = 8 + 8√2

D. P = 2 + 2√2

Câu 4: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1 ; 3) và B (4 ; 2). Tìm tọa độ của điểm C trên trục hoành sao cho khoảng cách từ C đến hai điểm A và B là như nhau

Câu 5: Trong mặt phẳng tọa độ Oxy, cho bốn điểm A (-1 ; 1), B (0 ; 2), C (3 ; 1) và D (0 ; -2). Khẳng định nào sau đây là chính xác?

A. Tứ giác ABCD là hình bình hành

B. Tứ giác ABCD là hình thoi

C. Tứ giác ABCD là hình thang cân

D. Tứ giác ABCD không phải là tứ giác nội tiếp đường tròn

Câu 6: Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 3) và B (4; 2). Tìm tọa độ của điểm C trên trục hoành sao cho khoảng cách từ C đến hai điểm A và B là như nhau

A. C (-5/3; 0)

B. C (5/3; 0)

C. C (-3/5; 0)

D. (3/5 ; 0)

Câu 7: Cho hình bình hành ABCD với tâm O. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a. Các cặp vectơ sau có cùng phương không: vectơ AB và vectơ MB; vectơ QM và vectơ BD; vectơ AD và vectơ MC

b. Xác định các vectơ cùng hướng và ngược hướng với vectơ MN

c. Tìm các vectơ bằng với vectơ OB

Câu 8: Cho tam giác ABC. Xây dựng các điểm M và N sao cho vectơ AM = vectơ BC và vectơ AN = vectơ CB. Hãy nhận xét về mối quan hệ giữa các vectơ AM và AN cũng như ba điểm A, M, N

Câu 9: Cho hình thang ABCD với các đáy AB và CD, trong đó AB = 2CD. Vẽ vectơ CI sao cho vectơ CI = vectơ DA

a. Chứng minh rằng I là trung điểm của AB và vectơ AI = vectơ CB

b. Chứng minh rằng vectơ AI = vectơ IB = vectơ DC

Câu 10: Cho tam giác đều ABC với cạnh AB = a. Kẻ đường cao AH

a. Gọi E và F là hai điểm trên cạnh BC sao cho BE = EF = FC. Tính tổng của các vectơ u = vectơ AB + vectơ EA + vectơ AC + vectơ FA

b. Xác định vectơ AH + BH và tính độ dài của vectơ AH + vectơ BH theo a

Câu 11: Cho tứ giác ABCD, với E và F lần lượt là trung điểm của các cạnh AB và CD, và O là trung điểm của EF. M là điểm tùy ý. Hãy chứng minh rằng

A. vectơ AD + vectơ BC = 2 vectơ EF

B. vectơ OA + vectơ OB + vectơ OC + vectơ OD = vectơ 0

C. vectơ AB + vectơ AC + vectơ AD = 4 vectơ AO

D. vectơ MA + vectơ MB + vectơ MC + vectơ MD = 4 vectơ MO

Câu 12: Cho tam giác ABC nội tiếp trong một đường tròn có tâm O, với H là trực tâm của tam giác và D là điểm đối xứng của A qua O.

a. Chứng minh rằng tứ giác BHCD là hình bình hành, từ đó suy ra vectơ HA + vectơ HB + vectơ HC = 2 vectơ HO

b. Chứng minh rằng vectơ OA + vectơ OB + vectơ OC = vectơ OH

c. Giả sử G là trọng tâm của tam giác ABC. Chứng minh rằng vecto OH = 3 vecto OG. Từ đó rút ra kết luận về ba điểm O, H, G.

Câu 13: Cho hình thoi ABCD với tâm O, cạnh bằng 4a, BD = 4a, và I là trung điểm của OC.

a. Tính độ dài của các vecto BO + vecto BC - 2 vecto CI, và vecto AB - vecto BC.

b. Tìm điểm M trên CD sao cho vecto MO + vecto MC + 2 vecto IA có độ dài nhỏ nhất.

Câu 14: Xét tam giác ABC.

a. Xác định điểm M sao cho vecto AM tương đương với vecto BC.

b. Xác định điểm N sao cho vecto BN bằng -2 vecto AC.

Câu 15: Trong tam giác ABC, I là điểm trên cạnh BC sao cho 2 CI = 3 BI. F là điểm trên cạnh BC kéo dài sao cho 5 FB = 2 FC.

a. Phân tích vecto AI và vecto AF theo vecto AB và vecto AC.

b. Giả sử G là trọng tâm của tam giác ABC. Tính độ dài của vecto AG dựa trên vecto AI và vecto AF.

Bài viết trên Mytour đã cung cấp thông tin chi tiết về cách tính độ dài vecto một cách đơn giản và dễ hiểu. Cảm ơn bạn đọc đã quan tâm theo dõi.

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]