1. Đạo hàm là gì?
Đạo hàm không phải là một khái niệm quá khó, nhưng đối với nhiều học sinh, nó có thể là một phần thách thức, đặc biệt là trong kỳ thi tốt nghiệp THPT quốc gia. Việc hiểu rõ đạo hàm sẽ giúp bạn vượt qua kỳ thi tốt hơn và học tập hiệu quả hơn.
Vậy công thức đạo hàm đầy đủ là gì? Để học tốt bất kỳ môn học hay bài tập nào, bạn cần nắm vững lý thuyết cơ bản, và điều này cũng áp dụng cho đạo hàm. Hiểu rõ đạo hàm là bước đầu tiên quan trọng.
Theo định nghĩa toán học, đạo hàm là tỷ lệ giữa sự thay đổi của biến số và sự thay đổi của hàm số tại một điểm cụ thể gọi là XO. Sự thay đổi lên xuống của hàm số tương ứng với giá trị của đạo hàm, giải thích tại sao đạo hàm quan trọng trong vật lý và các ứng dụng hình học và hình học không gian. Wikipedia cũng định nghĩa đạo hàm là sự thay đổi của hàm số tại điểm biến thiên.
Trong vật lý, đạo hàm biểu thị vận tốc tức thời, tức là tốc độ chuyển động của một chất tại một thời điểm cụ thể, và nó cũng thể hiện hình học trên đồ thị của hàm số.
Ý nghĩa của đạo hàm
Về mặt hình học: Đạo hàm của hàm số f(x) tại điểm x0 là hệ số góc của tiếp tuyến tại điểm M(x0,f(x0)).
=> Phương trình của tiếp tuyến tại điểm M: y−y0 = f′(x0)(x−x0)
Trong vật lý: Khi nghiên cứu chuyển động thẳng, s = f(t)
Vận tốc tức thời tại thời điểm t0 là: v(t0) = s′(t0) = f′(t0)
Gia tốc tức thời tại thời điểm t0 là đạo hàm cấp 2 của phương trình chuyển động: a(t0) = f′′(t0)
Nếu điện lượng Q truyền qua dây dẫn được mô tả bằng phương trình: Q = f(t)
Cường độ dòng điện tức thời tại thời điểm t0 là: I(t0) = Q′(t0) = f′(t0)
2. Công thức để tính đạo hàm
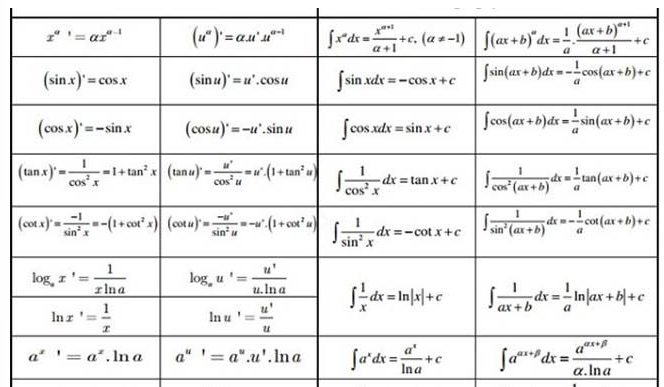
- Những công thức cơ bản để tính đạo hàm
+ Đối với hàm số y = xn (với n ∈ N, n > 1), đạo hàm của hàm số này tại mọi x ∈ R được tính bằng: (xn)′ = n xn – 1.
Dựa trên công thức tính đạo hàm:
(C)’ = 0 (với C là một hằng số). (x)’ = 1.
- Đạo hàm trong các phép toán với hàm số
Cho u = u(x) và v = v(x) là các hàm số có đạo hàm tại điểm x,
ta có: (u + v)′ = u′ + v′;
(u – v)′ = u′ – v′;
(u.v)′ = u′.v + u.v′;
(u/v)′ = (u′v − uv′) / v2, với v(x) ≠ 0
- Công thức mở rộng cho các hàm số
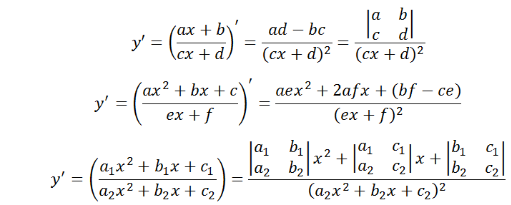
Công thức đạo hàm cho tổng các hàm số: (u1 + u2 + … + un)′ = u1 ′+ u2′ + … + un′.
+ Hệ quả 1: Nếu k là một hằng số, thì: (ku)’ = ku’.
+ Hệ quả 2: (1/v)′ = v′/v2, với v(x) ≠ 0
(u.v.w)′ = u′.v.w + u.v′.w + u.v.w′
- Đạo hàm của hàm hợp
Nếu hàm số y = f(u) với u = u(x), thì đạo hàm của y là: y′ = y′u . u′x.
Đạo hàm của (un) là n.un – 1.u′, với n thuộc N∗.
Đạo hàm của (u−√u) là u′2u√u.
- Bảng đạo hàm của hàm số biến x
Đạo hàm của (xα) là α.xα-1
Đạo hàm của (sin x) là cos x
Đạo hàm của (cos x) là – sin x
Đạo hàm của (tan x) là 1/cos^2 x = 1 + tan^2 x
Đạo hàm của (cot x) là −1/sin^2 x = −(1 + cot^2 x)
Đạo hàm của (logα x) là 1/(x.lnα)
Đạo hàm của (ln x) là 1/x, và (αx)’ = α/x . lnα
- Bảng đạo hàm của hàm số với biến là u = f(x)
Đạo hàm của (uα) là α.u’.uα-1
Đạo hàm của (sin u) là u’.cos u
Đạo hàm của (cos u) là – u’.sin u
Đạo hàm của (tan u) là u′/cos^2 u = u'(1 + tan^2 u)
Đạo hàm của (cot u) là −u/sin^2 u = -u'(1 + cot^2 u)
Đạo hàm của (logα u) là 1/(u.lnα)
Đạo hàm của (ln u) là u′/u, và (αu)’ = u’.αu.lnα
Đạo hàm của (eu) là u’.eu
- Các công thức đạo hàm nâng cao
Giả sử hàm số y = f(x) có đạo hàm cấp n-1 ký hiệu là f^(n-1)(x) (với n ∈ N và n ≥ 4).
Nếu f^(n-1)(x) có đạo hàm, thì đạo hàm của nó được gọi là đạo hàm cấp n của y = f(x), ký hiệu là y^(n) hoặc f^(n)(x).
f^(n)(x) = [f^(n-1)(x)]’
Công thức đạo hàm cấp cao:
Nếu m ≥ n, thì ta có: (x^m)^(n) = m(m – 1)(m – 2)…(m – n + 1).x^(m – n)
Nếu m ≤ n, thì ta có: (x^m)^(n) = 0
3. Một số bài tập cơ bản về đạo hàm
Bài tập 1: Tính đạo hàm của hàm số y = x^3 – 3x^2 + 2x + 1
Giải: Áp dụng công thức đạo hàm, ta có: y′ = (x^3 – 3x^2 + 2x + 1)′ = 3x^2 – 6x + 2
Bài tập 2: Tính đạo hàm của hàm số chứa căn y = (2x + 1)/(x – 3)
Giải
Áp dụng công thức đạo hàm cho hàm hợp:
y′ = [(2x + 1)′(x – 3) – (x – 3)′(2x + 1)] / (x – 3)^2
= –7 / (x – 3)^2
Bài tập 3: Đạo hàm của hàm số y = (2x^4 – 3x^2 – 5x)(x^2 – 7x) là biểu thức nào dưới đây?
A. (8x^3 – 6x – 5)(2x – 7)
B. (8x^3 – 6x – 5)(x^2 – 7x) – (2x^4 – 3x^2 – 5x)(2x – 7)
C. (8x^3 – 6x – 5)(x^2 – 7x) + (2x^4 – 3x^2 – 5x)(2x – 7)
D. (8x^3 – 6x – 5) + (2x – 7)
Giải
Đáp án: C
Áp dụng công thức đạo hàm cho hàm hợp (uv)’ = u’v + uv’
Ta có: y′ = (8x^3 – 6x – 5)(x^2 – 7x) + (2x^4 – 3x^2 – 5x)(2x – 7)
Chọn đáp án C
Bài tập 4: Tính đạo hàm của hàm số f(t) = a^3t^4 – 2at^2 + 3t – 5a và chọn biểu thức tương ứng
A. 4a^3t^3 – 4at + 3
B. 3a^2t^4 – 2t^2 – 5
C. 12a^2t^3 – 4at – 2
D. 4a^3t^3 – 4at – 5
Giải: Đáp án là A, f'(t) = 4a^3t^3 – 4at + 3
Chọn đáp án A
Bài tập 5: Tính đạo hàm của hàm số f(x) = a^3 – 3at^2 – 5t^3 (với a là hằng số) và chọn biểu thức phù hợp
A. 3a^2 – 6at – 15t^2
B. 3a^2 – 3t^2
C. -6at – 15t^2
D. 3a^2 – 3t^2 – 6at – 15t^2
Giải: Đáp án là C
f(t) = a^3 – 3at^2 – 5t^3, và f'(t) = -6at – 15t^2
Chọn đáp án C
Bài tập 6: Tính đạo hàm của hàm số y = 6(sin^4 x + cos^4 x) – 4(sin^6 x + cos^6 x) và chọn biểu thức tương ứng
A. 24(sin^3 x + cos^3 x) – 24(sin^5 x + cos^5 x)
B. 24(sin^3 x – cos^3 x) – 24(sin^5 x + cos^5 x)
C. 2
D. 0
Giải
Đáp án: D
y’ = 6(sin^2 x + cos^2 x)^2 – 12sin^2 x cos^2 x – 4(sin^2 x + cos^2 x)^2 + 12sin^2 x cos^2 x(sin^2 x + cos^2 x) = 2
Bài tập 7: Tính đạo hàm của hàm số y = (5x + 2)^10
A. 10(5x + 2)^9
B. 50(5x + 2)^9
C. 5(5x + 2)^9
D. (5x + 2)^9
Giải
Đạo hàm của hàm số là: y’ = 10.(5x + 2)^9.(5x + 2)’ = 50(5x + 2)^9
Chọn đáp án B
Bài tập 8:
Tính đạo hàm của hàm số y = f(x) = (1 – 3x^2)^5
A. -30x.(1 – 3x^2)^4
B. -10x.(1 – 3x^2)^4
C. 30(1 – 3x^2)^4
D. -3x.(1 – 3x^2)^4
Giải
Đặt u(x) = 1 – 3x^2
Suy ra u'(x) = (1 – 3x^2)’ = 0 – 3(2x) = -6x
Với u = 1 – 3x^2, thì y = u^5, suy ra y’ = 5u^4 = 5(1 – 3x^2)^4
Áp dụng công thức đạo hàm của hàm hợp, ta có: y’(x) = 5.(1 – 3x^2)^4.(-6x) = -30x.(1 – 3x^2)^4
Chọn đáp án A.
Bài tập 9: Tính đạo hàm của hàm số: y = (x^3 + x^2 - 1)^2 (2x + 1)^2
A. y’ = (x^3 + x^2 - 1)(3x^2 + 2x).(2x + 1)^2 + (x^3 + x^2 - 1)^2.(8x + 4)
B. y’ = 2(x^3 + x^2 - 1)(3x^2 + 2x).(2x + 1)^2 + (x^3 + x^2 - 1)^2.(8x + 4)
C. y’ = (x^3 + x^2 - 1)(3x^2 + 2x).(2x + 1)^2 + (x^3 + x^2 - 1)^2.(4x + 4)
D. y’ = 2(x^3 + x^2 - 1)(3x^2 + 2x).(2x + 1)^2 - (x^3 + x^2 - 1)^2.(8x + 4)
Giải
Áp dụng công thức đạo hàm của hàm hợp và đạo hàm của tích, ta có: y’ = [(x^3 + x^2 - 1)^2]’.(2x + 1)^2 + (x^3 + x^2 - 1)^2.[(2x + 1)^2]’
Vậy y’ = 2(x^3 + x^2 - 1)(x^3 + x^2 - 1)’.(2x + 1)^2 + (x^3 + x^2 - 1)^2.2(2x + 1).(2x + 1)’
⇔ y’ = 2(x^3 + x^2 - 1)(3x^2 + 2x).(2x + 1)^2 + (x^3 + x^2 - 1)^2.2(2x + 1).2
⇔ y’ = 2(x^3 + x^2 - 1)(3x^2 + 2x).(2x + 1)^2 + (x^3 + x^2 - 1)^2.(8x + 4)
Bài tập 10: Tìm số nghiệm của phương trình y’ = 0 với hàm số y = 2x^3 – 6x^2 + 2000.
A. 0
B. 1
C. 2
D. 3
Giải
+ Đạo hàm của hàm số là: y’ = 6x^2 - 12x
+ Để phương trình y’ = 0 thì ta có 6x^2 - 12x = 0
Chọn C.
Bài tập 11: Xét hàm số y = x^4 + 2x^3 - kx^2 + x - 10. Tìm giá trị của k sao cho phương trình y’ = 1 có nghiệm x = 1?
A. k = 5
B. k = -5
C. k = 2
D. k = -3
Giải
+ Đạo hàm của hàm số là: y’ = 4x^3 + 6x^2 - 2kx + 1.
+ Để y’ = 1 thì 4x^3 + 6x^2 - 2kx + 1 = 1, suy ra 4x^3 + 6x^2 - 2kx = 0. ()
Vì phương trình y’ = 1 có nghiệm x = 1, nên phương trình () cũng có nghiệm x = 1.
Từ đó, 4.1^3 + 6.1^2 - 2k.1 = 0 suy ra 10 - 2k = 0, nên k = 5.
Chọn A.
Trân trọng!
