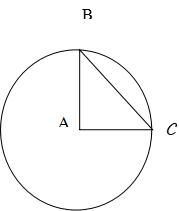
1. Khái niệm chu vi hình tròn
Hình tròn là một khái niệm cơ bản trong hình học, đại diện cho tập hợp các điểm nằm trên và trong đường tròn, tất cả đều cách điểm trung tâm một khoảng cách cố định. Với tính đồng đều và cân bằng, hình tròn thường được sử dụng để biểu thị sự hoàn hảo trong toán học và nhiều lĩnh vực khác.
Hình tròn và đường tròn là những khái niệm cơ bản trong hình học, với sự khác biệt chính nằm ở cách chúng được định nghĩa và mô tả.
Hình tròn là tập hợp tất cả các điểm nằm trên và bên trong một đường tròn. Nói cách khác, hình tròn gồm tất cả các điểm cách điểm trung tâm một khoảng cách không lớn hơn bán kính. Bán kính của hình tròn chính là khoảng cách từ trung tâm đến bất kỳ điểm nào trên đường tròn. Tức là, bán kính là độ dài của đoạn thẳng nối trung tâm với bất kỳ điểm nào trên hình tròn.
Trong khi đó, đường tròn được định nghĩa là tập hợp tất cả các điểm nằm trên một mặt phẳng và cách một điểm cố định (tâm đường tròn) một khoảng cách cố định bằng bán kính. Bán kính của đường tròn là khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn. Đường tròn không chỉ bao gồm các điểm trên nó, mà còn khác với hình tròn vì không có các điểm nằm bên trong.
Một điểm cần lưu ý là đường tròn không có diện tích, khác với hình tròn. Mặc dù đường tròn gần giống hình tròn, nhưng nó không có diện tích cụ thể.
Để mô tả một đường tròn, chúng ta cần hai yếu tố chính: tâm và bán kính. Đường tròn có tâm là O và bán kính là R, bao gồm tất cả các điểm cách tâm O một khoảng cách bằng R. Bất kỳ điểm nào nằm trên đường tròn và nối trực tiếp với tâm O đều là bán kính.
Quy tắc tính chu vi của hình tròn là nhân đường kính với số 3,14.
C = d x 3,14
(Trong đó, C là chu vi của hình tròn và d là đường kính của nó).
Hoặc: Để tính chu vi của hình tròn, ta nhân hai lần bán kính với số 3,14.
C = r x 2 x 3,14
(Trong đó, C là chu vi của hình tròn và r là bán kính của nó).
2. Giải bài tập Toán lớp 5, bài 95: Tính chu vi hình tròn một cách chi tiết
Bài 95, Vở bài tập Toán lớp 5, tập 2 - Câu 1
Điền số đo phù hợp vào các ô trống:
| Hình tròn | (1) | (2) | (3) |
| Đường kính | 1,2cm | 1,6dm | 0,45m |
| Chu vi |
Phương pháp giải:
Để tính chu vi của hình tròn, ta nhân đường kính với hằng số 3,14.
C = d × 3,14
(C đại diện cho chu vi hình tròn, d là đường kính của hình tròn).
Kết quả
Chu vi hình tròn (1): C = d × 3,14 = 1,2 × 3,14 = 3,768 cm
Chu vi hình tròn (2): C = 1,6 × 3,14 = 5,024 dm
Chu vi hình tròn (3): C = 0,45 × 3,14 = 1,413 m
Do đó, chúng ta có bảng kết quả như sau:
| Hình tròn | (1) | (2) | (3) |
| Đường kính | 1,2cm | 1,6dm | 0,45m |
| Chu vi | 3,768cm | 5,024dm | 1,413m |
Vở bài tập Toán lớp 5 tập 2 bài 95 Câu 2
Câu 2. Điền số thích hợp vào các ô trống:
| Hình tròn | (1) | (2) | (3) |
| Bán kính | 5m | 2,7dm | 0,45cm |
| Chu vi |
Cách giải:
Để tính chu vi hình tròn, chúng ta nhân gấp đôi bán kính với số 3,14.
C = r × 2 × 3,14
(C là chu vi hình tròn, r là bán kính của hình tròn)
Kết quả
Chu vi hình tròn (1): C = d × 3,14 = r × 2 × 3,14 = 5 × 2 × 3,14 = 31,4 m
Chu vi hình tròn (2): C = 2,7 × 2 × 3,14 = 16,956 dm
Chu vi hình tròn (3): C = 0,45 × 2 × 3,14 = 2,826 cm
Kết quả được tổng hợp như sau:
| Hình tròn | (1) | (2) | (3) |
| Bán kính | 5m | 2,7dm | 0,45cm |
| Chu vi | 31,4m | 16,956dm | 2,826cm |
Vở bài tập Toán lớp 5 tập 2 bài 95 Câu 3
Tính chu vi của bánh xe nhỏ trên đầu máy xe lửa, có đường kính 1,2m.
Cách giải quyết:
Để tính chu vi của bánh xe, chúng ta nhân đường kính với 3,14.
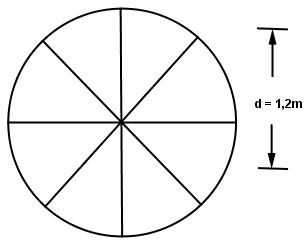
Giải quyết bài toán
Chu vi của bánh xe là:
1,2 × 3,14 = 3,768 (m)
Kết quả: 3,768m
3. Bài tập áp dụng tính chu vi hình tròn lớp 5
Bài 1: Tính chu vi của các hình tròn sau:
a, d = 3cm b, d = 4,5m
Bài 2: Tính chu vi của các hình tròn với các thông số sau:
a, r = 2,5cm b, r = 4cm
Bài 3: Một sợi dây thép được cuộn thành hình tròn với bán kính 7cm. Tính chiều dài của sợi dây thép.
Bài 4: Tính diện tích của các hình tròn sau:
a, r = 5 cm b, r = 3,3m
Bài 5: Tính diện tích của các hình tròn với các thông số sau:
a, d = 7cm b, d = 12dm
Bài 6: Xác định bán kính của các đường tròn có chu vi lần lượt là 18,84cm và 25,12dm.
Bài 7: Tìm đường kính của các hình tròn có chu vi lần lượt là 15,7dm và 21,98cm.
Bài 8: Một biển báo giao thông hình tròn có đường kính 40cm. Diện tích của mũi tên chỉ đường chiếm 1/5 diện tích của biển báo. Tính diện tích còn lại của biển báo.
Bài 9: Ở đầu xóm, một cái giếng có miệng hình tròn với đường kính 1,6m đã được đào. Xung quanh miệng giếng, người ta xây một thành rộng 0,3m. Tính diện tích của thành giếng.
Bài 10: Trong sân trường, có hai bồn hoa hình tròn. Bồn hoa cúc có đường kính 40dm, còn bồn hoa hồng có chu vi 9,42m. Hãy xác định bồn hoa nào có diện tích lớn hơn và hơn bao nhiêu dm².
Bài 11: Tính chu vi và diện tích của các hình tròn với các thông số sau:
a) r = 5cm ; r = 0,8cm ; r = 4/5 dm.
b) d = 5,2m ; d = 1,2m ; d = 3/5 dm.
Bài 12: Tính đường kính của các hình tròn với chu vi lần lượt là: C = 12,56cm; C = 18,84dm; C = 2,826m.
Bài 13: Xác định bán kính của các hình tròn có chu vi: C = 16,328dm; C = 8,792cm; C = 26,376m.
Bài 14: Tính diện tích của các hình tròn với chu vi: C = 6,908m; C = 25,12dm; C = 16,956cm.
Bài 15: Một bảng chỉ đường hình tròn có đường kính 50cm.
a. Tính diện tích của bảng chỉ đường này tính theo mét vuông?
b. Nếu sơn cả hai mặt của tấm bảng, mỗi mét vuông hết 7000 đồng. Tính tổng chi phí để sơn toàn bộ tấm bảng?
Bài 16: Một biển báo giao thông hình tròn với đường kính 40cm. Phần mũi tên trên biển báo chiếm 1/5 diện tích của biển báo. Tính diện tích của phần mũi tên?
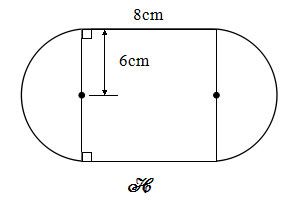
Bài 17: Diện tích hình H là tổng của diện tích hình chữ nhật và hai nửa hình tròn. Tính diện tích của hình H.
Bài 18: Xét hình vuông ABCD với cạnh dài 4cm. Tính diện tích của phần được tô đậm trong hình vuông ABCD (theo hình minh họa).
.jpg)
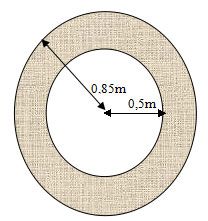
Bài 19: Tính diện tích của phần tô đậm giữa hai hình tròn đồng tâm O với bán kính lần lượt là 0,8m và 0,5m (xem hình minh họa).
Bài 20: Cho hình tròn với tâm O và đường kính AB dài 8cm.
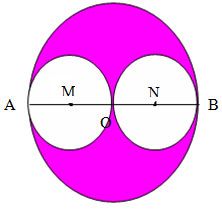
a) Tính chu vi của các hình tròn có tâm O với đường kính AB, tâm M với đường kính OA và tâm N với đường kính OB.
b) So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi của hình tròn tâm O.
Bài 21: Một cái nong hình tròn có chu vi 376,8cm. Tính diện tích của cái nong theo mét vuông.
Bài 22: Sân trường của bạn có hình chữ nhật với chiều dài 45m và chiều rộng lớn hơn 6,5m. Giữa sân có một bồn hoa hình tròn có đường kính 3,2m. Tính diện tích còn lại của sân trường.
Bài 23: Ở đầu xóm, có một cái giếng với miệng hình tròn đường kính 1,6m. Xung quanh miệng giếng có một thành rộng 0,3m. Hãy tính diện tích của thành giếng.
Bài 24: Tính diện tích của tam giác vuông ABC trong hình vẽ, biết rằng hình tròn với tâm A có chu vi 37,68 cm.