1. Khái niệm về hình thoi
Hình thoi là một loại hình học đặc biệt với bốn đỉnh tạo thành hai cặp đường chéo bằng nhau và tổng độ dài các cạnh đều bằng nhau. Điểm giao nhau của hai đường chéo là trung tâm của hình thoi, đồng thời là tâm đối xứng. Một số đặc điểm của hình thoi bao gồm:
- Các cạnh đối diện của hình thoi song song và bằng nhau; tổng các góc trong hình thoi là 360 độ, với mỗi góc đều bằng nhau và là 90 độ.
- Đường chéo của hình thoi kết nối các đỉnh đối diện và cắt nhau vuông góc tại trung tâm. Hình thoi có hai trục đối xứng, mỗi trục chia hình thoi thành hai phần bằng nhau.
- Diện tích của hình thoi được tính bằng một nửa tích của hai độ dài đường chéo. Công thức tính diện tích là: diện tích = (độ dài đường chéo 1 x độ dài đường chéo 2) / 2.
Hình thoi là một trong những hình học phổ biến và có nhiều ứng dụng trong các lĩnh vực khác nhau. Một số ứng dụng tiêu biểu bao gồm:
- Trang trí và nghệ thuật: Hình thoi thường được sử dụng như một yếu tố trang trí trong thiết kế nội thất, họa tiết trên vải, tranh vẽ đồ họa. Sự kết hợp của các hình thoi có thể tạo ra các mẫu thiết kế đẹp mắt và thu hút.
- Kỹ thuật và xây dựng: Trong ngành kỹ thuật và xây dựng, hình thoi thường xuất hiện trong các cấu trúc chịu lực như khung xương, hệ thống chịu tải, và các bề mặt đồng phẳng. Hình thoi cũng có thể được dùng làm hình dạng cho cửa sổ hoặc cửa trượt.
- Toán học: Trong toán học, hình thoi được nghiên cứu và ứng dụng trong nhiều vấn đề hình học như tính diện tích, chu vi, và các đặc điểm của nó như các góc vuông và các trục đối xứng.
- Địa lý: Hình thoi có thể được dùng để mô tả hình dạng của một số cấu trúc tự nhiên như mỏ kim cương hoặc hòn đảo.
- Kỹ thuật đo lường: Hình thoi có thể được áp dụng trong các thiết bị đo lường, chẳng hạn như đo diện tích không gian.
- Trò chơi: Hình thoi xuất hiện trong một số trò chơi như một phần của thiết kế trò chơi.
- Công nghệ thông tin: Trong công nghệ thông tin, hình thoi được áp dụng trong các thuật toán và mã hóa.
2. Vở bài tập toán lớp 4
Bài 1: Đánh dấu vào ô trống dưới hình thoi có diện tích nhỏ hơn 20 cm²
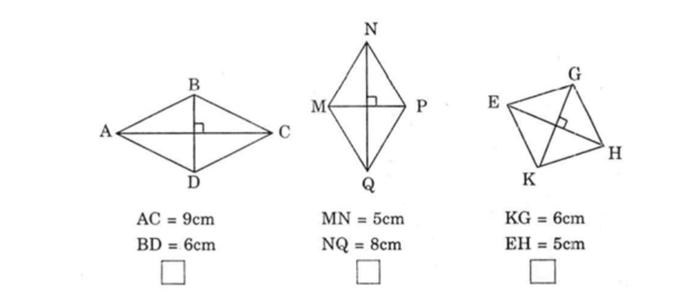
Phương pháp giải: Tính diện tích của hình thoi rồi so sánh với 20 cm² để chọn đúng.
Diện tích hình thoi được tính bằng cách nhân độ dài hai đường chéo rồi chia đôi, với công thức S = (m x n) / 2 hoặc S = (m x n) : 2
S đại diện cho diện tích của hình thoi
m và n là các độ dài của hai đường chéo
Kết quả:
Diện tích của hình thoi ABCD được tính là 9 x 6 : 2 = 27 cm².
Diện tích của hình thoi MNPQ được tính là 5 x 8 : 2 = 40 cm².
Diện tích hình thoi EGHK là 6 x 5 : 2 = 15 cm².
Do đó, hình thoi có diện tích nhỏ hơn 20 cm² là EGHK.
Bài 2:
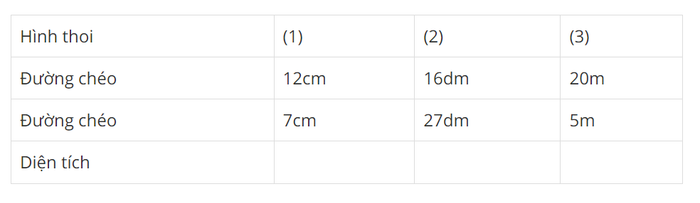
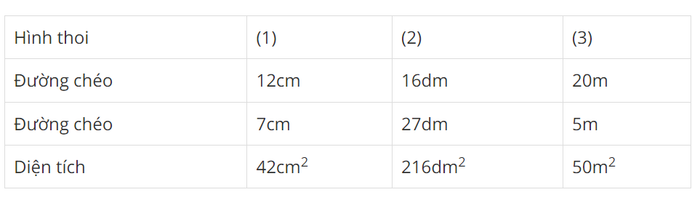
Bài 3: Tính diện tích của một mảnh bìa hình thoi có hai đường chéo dài 10 cm và 24 cm.
Để tính diện tích của mảnh bìa, ta nhân độ dài hai đường chéo với nhau và chia kết quả cho 2.
Diện tích của mảnh bìa là (10 x 24) / 2 = 120 cm².
3. Bài tập bổ sung
Câu 1: Đánh dấu Đ cho đúng và S cho sai.
Xem xét hình thoi ABCD
a. AB song song với DC
b. AB vuông góc với BC
c. Chỉ có một cặp cạnh đối diện song song là AB và CD
d. AB = BC = CD = DA
Câu 2: Xem xét các hình dưới đây
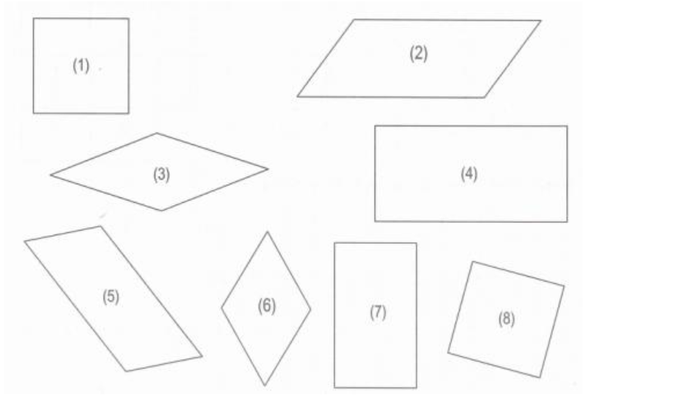
a. Hình nào là hình thoi?
b. Hình nào là hình bình hành?
c. Hình nào là hình chữ nhật?
d. Hình nào là hình vuông?
Câu 3: Điền vào chỗ trống
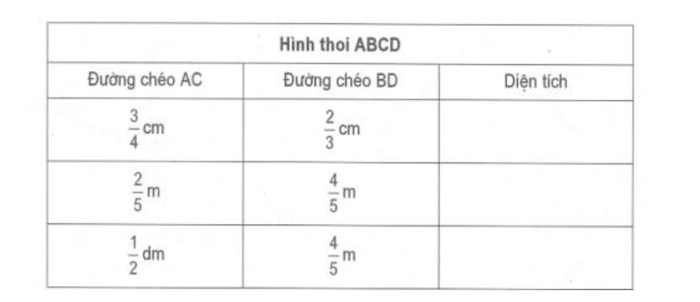
Câu 4: Một hình thoi có diện tích 4 dm² và một đường chéo dài 3/5 dm. Tìm độ dài của đường chéo còn lại.
Câu 5: Tính diện tích của một khu đất hình thoi với các đường chéo dài 70 m và 300 m.
Câu 6: Khoanh vào chữ đứng trước hình có diện tích lớn nhất.
A. Hình vuông có cạnh dài 5 cm
B. Hình chữ nhật có chiều dài 6 cm và chiều rộng 4 cm
C. Hình bình hành có diện tích 20 cm²
D. Hình thoi có các đường chéo dài 10 cm và 6 cm
Kết quả:
Câu 1: S, S, S, D
Câu 2: Các hình thoi là hình 3 và 6
Hình bình hành là các hình 2 và 5
Các hình chữ nhật là hình 4 và 7
Các hình vuông là hình 1 và 8
Câu 4: Các số diện tích lần lượt là 1/4 cm², 4/25 m², 2 dm²
Câu 5: Độ dài đường chéo còn lại là (4 x 2) : 3/5 = 40/3 dm
Câu 6: Diện tích khu đất là 70 x 300 / 2 = 10.500 m²
Câu 7: D
Câu 8: Tính diện tích của hình thoi khi biết độ dài hai đường chéo
a. 12 cm và 8 cm
b. 3 m 5 dm và 4 m
Đáp án:
a. Diện tích hình thoi được tính bằng công thức (12 x 8) / 2 = 48 cm².
b. Chuyển đổi 3 m 5 dm thành 35 dm.
4 m đổi thành 40 dm.
Diện tích hình thoi là (35 x 40) / 2 = 700 dm².
Câu 9: Một hình thoi có tổng chiều dài hai đường chéo là 45 cm. Nếu đường chéo thứ nhất bằng 3/2 đường chéo thứ hai, tính diện tích của hình thoi đó.
Tổng số phần bằng nhau là 3 + 2 = 5/4.
Độ dài đường chéo thứ nhất là 45 / 5 x 3 = 27 cm.
Chiều dài đường chéo thứ hai là 45 - 27 = 18 cm.
Diện tích hình thoi tính được là (27 x 18) / 2 = 243 cm².
Câu 10: Một khu đất hình thoi có cạnh dài 42 m. Để bao quanh khu đất bằng 4 dây kẽm gai, tổng chiều dài dây cần dùng là bao nhiêu mét?
Kết quả: Chu vi khu đất hình thoi là 42 x 4 = 168 m.
Tổng chiều dài dây kẽm cần thiết để rào xung quanh khu đất là 168 x 4 = 672 m.
Câu 11: Hình chữ nhật ABCD có chu vi là 22 m, với chiều dài nhiều hơn chiều rộng 3 m. Tính diện tích của hình thoi MNPQ.
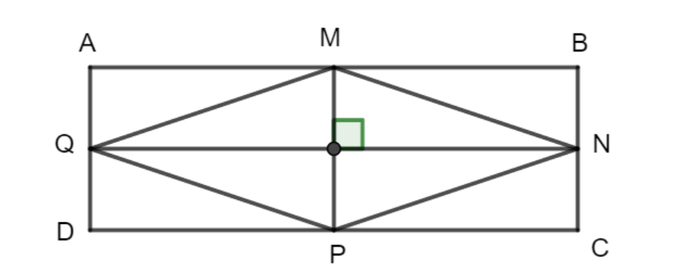
Đáp án
Nửa chu vi của hình chữ nhật là 22:2 = 11 m.
Chiều rộng của hình chữ nhật ABCD là 11 - 3/2 = 4 cm.
Chiều dài của hình chữ nhật ABCD là 4 + 3 = 7 cm.
Đối với hình thoi MNPQ, đường chéo QN = AB = 7 cm.
Với đường chéo MP = BC = 4 cm, diện tích hình thoi là (7 x 4) : 2 = 14 cm².
Câu 12: Xác định diện tích hình chữ nhật MPOA, biết rằng hình thoi ABCD có diện tích 48 cm² và đường chéo AC dài 12 cm.
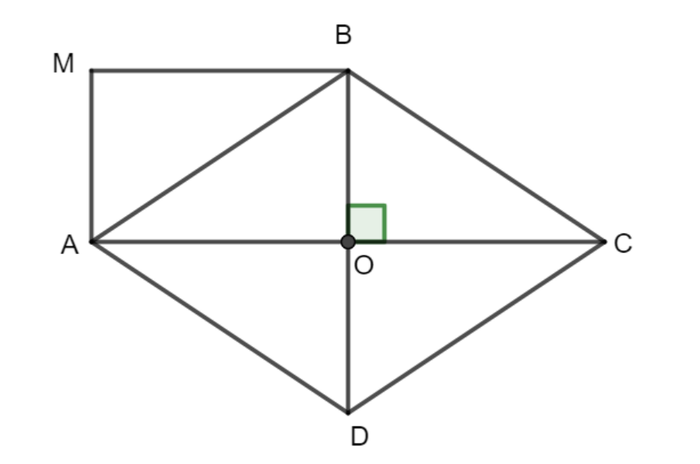
Đoạn đường chéo BD của hình thoi ABCD tính được là (48 x 2) / 12 = 8 cm.
Chiều dài đoạn BO là 8 : 2 = 4 cm.
Chiều dài đoạn AO là 12 : 2 = 6 cm.
Diện tích hình chữ nhật MBOA là 6 x 4 = 24 cm².
Câu 13: Xác định diện tích hình chữ nhật ABCD biết rằng hình thoi AMBN có diện tích 14 cm², đoạn MO dài 2 cm và chu vi hình chữ nhật ABCD là 22 cm.
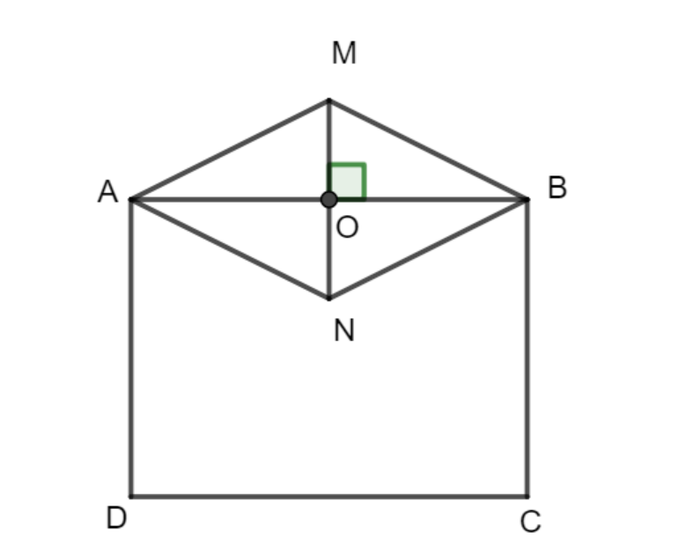
Đáp án:
Chiều dài đoạn MN được tính là 2 x 2 = 4 cm.
Chiều dài đoạn AB tính được là (14 x 2) : 4 = 7 cm.
Nửa chu vi của hình chữ nhật ABCD là 22 : 2 = 11 cm.
Chiều rộng AD của hình chữ nhật ABCD được tính là 11 - 7 = 4 cm.
Diện tích hình chữ nhật ABCD là 7 x 4 = 28 cm².
Câu 14: Trong hình thoi ABCD, O là giao điểm của hai đường chéo với OA = 9 cm và OB = 6 cm. Hãy xác định khẳng định đúng, biết rằng hai đường chéo của hình thoi vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường chéo.
A: Diện tích của hình thoi bằng diện tích của hình vuông.
B: Diện tích của hình thoi lớn hơn diện tích của hình vuông.
C: Diện tích của hình thoi nhỏ hơn diện tích của hình vuông.
D: Diện tích của hình thoi gấp đôi diện tích của hình vuông.
Đáp án: B
Khám phá Đề thi học kì 2 môn Toán lớp 4 của Mytour
