1. Tỉ số là gì?
Trong toán học, tỉ số hay tỷ lệ là một khái niệm quan trọng giúp chúng ta hiểu rõ hơn về mối quan hệ số học giữa các đối tượng hoặc đơn vị đo lường. Đây là công cụ hữu ích trong việc phân tích và so sánh dữ liệu, xuất hiện trong nhiều lĩnh vực từ tài chính đến khoa học xã hội và đời sống hàng ngày.
Tỉ số là cách biểu thị mức độ tương quan giữa hai giá trị số học. Nó cho biết một giá trị chiếm bao nhiêu lần giá trị kia. Ví dụ, nếu một giỏ trái cây có tám quả cam và sáu quả chanh, chúng ta sử dụng tỉ số để mô tả mối quan hệ giữa số cam và số chanh. Trong trường hợp này, tỉ số cam so với chanh là tám chia sáu, tương đương với 4:3. Tỉ số giúp chúng ta biểu thị và so sánh mối quan hệ giữa các số liệu một cách rõ ràng, đồng thời hỗ trợ trong việc thực hiện các phép tính và phân tích dữ liệu, từ đó ra quyết định hiệu quả trong nhiều tình huống phức tạp.
Tỉ số (hoặc tỉ lệ) là một khái niệm cốt lõi trong toán học và đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau. Dưới đây là những vai trò chính của tỉ số trong toán học:
- Biểu thị và phân tích mối quan hệ số học: Tỉ số là công cụ mạnh mẽ để biểu diễn và nghiên cứu mối quan hệ giữa các giá trị số. Nó cho phép chúng ta đánh giá mức độ ảnh hưởng của một giá trị đối với giá trị khác, hữu ích trong việc phân tích dữ liệu, nhận diện xu hướng, mối liên hệ và tương tác giữa các số liệu.
- Áp dụng trong phân số và toán tỷ lệ: Tỉ số là dạng đặc biệt của phân số, với tử số và mẫu số biểu thị hai giá trị và mối quan hệ của chúng. Tuy nhiên, khái niệm tỷ lệ cũng được mở rộng để tính toán các tỷ lệ phức tạp hơn trong hình học, vật lý và kỹ thuật, giúp so sánh kích thước, diện tích, thể tích và các thuộc tính khác.
- Tính toán tỷ lệ trong hình học: Trong hình học, tỉ số được sử dụng để tính toán tỷ lệ giữa các phần khác nhau của hình học như chiều dài, diện tích và thể tích. Điều này giúp xác định mối quan hệ giữa các yếu tố hình học, hỗ trợ trong việc vẽ biểu đồ, thiết kế và giải quyết các bài toán không gian.
- Ứng dụng trong tài chính và quản lý rủi ro: Tỉ số rất quan trọng trong tài chính, giúp đánh giá hiệu suất đầu tư, rủi ro tài chính và phân tích tài chính. Trong quản lý rủi ro, tỷ lệ cho phép đo lường và đánh giá các yếu tố liên quan đến lợi nhuận, nợ và các chỉ số quan trọng khác trong doanh nghiệp hoặc dự án.
- Ứng dụng trong dự đoán và lập kế hoạch chiến lược: Trong việc lập kế hoạch kinh doanh và dự đoán, tỉ số đóng vai trò quan trọng trong việc xác định xu hướng, dự báo kết quả và xây dựng chiến lược. Các tỷ số tài chính thường được dùng để đánh giá sự ổn định và bền vững của tổ chức trong tương lai. Tỉ số cũng hỗ trợ trong quản lý dự án và tài nguyên, dự đoán tình huống và nhận diện cơ hội.
- Ứng dụng đa dạng trong toán học ứng dụng và khoa học: Tỉ số có nhiều ứng dụng trong các lĩnh vực toán học ứng dụng như thống kê, khoa học xã hội, khoa học tự nhiên và công nghệ. Ví dụ, trong thống kê, tỉ số được dùng để thể hiện tỷ lệ phần trăm, xác định mối liên hệ giữa các biến và phân tích dữ liệu phức tạp. Trong khoa học xã hội, tỉ số giúp hiểu các xu hướng xã hội và kinh tế. Trong khoa học tự nhiên và công nghệ, tỉ số hỗ trợ đo lường các quá trình và hiện tượng phục vụ nghiên cứu và cải tiến.
2. Xác định hai số khi biết hiệu và tỉ số của chúng - bài 1
Điền số hoặc tỉ số vào chỗ trống:
a)
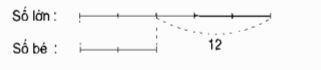
Hiệu giữa hai số là ….
Số lớn được chia thành … phần bằng nhau.
Số nhỏ được chia thành …. phần như vậy.
Tỉ lệ giữa số lớn và số nhỏ là ..........
Hiệu giữa các phần bằng nhau là … phần.
b)
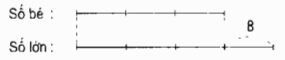
Hiệu của hai số là …
Số nhỏ được chia thành … phần bằng nhau.
Số lớn được chia thành …. phần tương ứng.
Tỉ lệ giữa số nhỏ và số lớn là …
Hiệu của các phần bằng nhau là … phần.
Hướng dẫn để hoàn thành bài tập:
Đầu tiên, hãy xem xét kỹ lưỡng sơ đồ được cung cấp để đảm bảo bạn hiểu rõ yêu cầu. Sau đó, áp dụng kiến thức và kỹ năng của bạn để giải quyết bài tập một cách logic và hiệu quả. Hãy thực hiện đầy đủ các bước cần thiết và kiểm tra kết quả cuối cùng để đảm bảo tính chính xác và hoàn chỉnh.
Giải pháp:
a) Trước tiên, chúng ta cần tìm hai số có hiệu là 12. Trong tình huống này, số lớn được chia thành 5 phần, trong khi số nhỏ được chia thành 2 phần. Để xác định tỷ lệ giữa số lớn và số nhỏ, ta chia số lớn cho số nhỏ, kết quả là 5 chia 2, tương đương với 5/2. Hiệu số giữa các phần bằng nhau là 3 phần.
b) Đầu tiên, cần xác định hiệu của hai số, theo bài toán là 8. Số nhỏ được chia thành 3 phần, trong khi số lớn được chia thành 4 phần. Để tính tỷ lệ giữa số nhỏ và số lớn, ta chia số nhỏ cho số lớn, kết quả là 3 chia 4, tương đương với 3/4. Hiệu số giữa các phần bằng nhau là 1 phần, điều này có thể được tính bằng cách lấy số nhỏ trừ số lớn, kết quả là 3 trừ 4 bằng 1.
3. Xác định hai số khi biết hiệu và tỷ lệ giữa chúng - bài 2
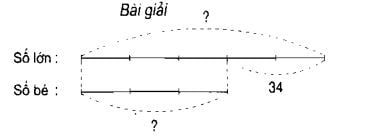
Hiệu giữa hai số là 34. Tỷ lệ giữa hai số là 5/3. Tìm hai số đó.
Dưới đây là sơ đồ:
Hướng dẫn giải bài toán:
Để giải bài toán này, chúng ta thực hiện các bước sau đây:
- Bước 1: Xác định hiệu của hai số, đây là yếu tố quan trọng trong bài toán. Bạn cần phải biết số phần bằng nhau của hiệu số.
- Bước 2: Sau khi đã biết hiệu của hai số, bạn sẽ tìm giá trị của một phần bằng cách chia hiệu của hai số cho số phần bằng nhau. Điều này giúp bạn xác định chính xác giá trị của từng phần trong tổng.
- Bước 3: Tiếp theo, xác định giá trị của số bé bằng cách nhân giá trị của một phần với số phần của số bé. Bước này giúp bạn tính ra số bé dựa trên hiệu và số phần đã biết.
- Bước 4: Cuối cùng, tính giá trị của số lớn bằng cách cộng số bé với hiệu của hai số. Điều này cho phép bạn xác định số lớn dựa trên các thông tin đã có từ các bước trước.
Lưu ý: Mặc dù bước 2 và bước 3 có thể được gộp lại, việc thực hiện chúng riêng biệt giúp quy trình giải bài toán trở nên rõ ràng và dễ hiểu hơn.
Kết quả:
- Từ sơ đồ, chúng ta tính hiệu số phần bằng nhau bằng cách lấy số phần của số lớn (5 phần) trừ đi số phần của số bé (3 phần), kết quả là 2 phần.
- Để tìm số lớn, ta nhân hiệu số phần (2 phần) với số phần của số lớn (5 phần). Kết quả là 2 nhân 5 bằng 10 phần. Sau đó, thêm số này vào số bé để xác định số lớn.
- Để xác định số bé, ta lấy hiệu của hai số (85 phần) trừ đi số lớn đã tính được (10 phần). Kết quả là 85 trừ 10 bằng 75, đó chính là số bé.
Kết quả cuối cùng: Số lớn là 85 và số bé là 75.
4. Xác định hai số khi biết hiệu và tỷ lệ giữa chúng - bài 3
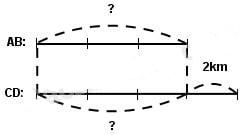
Đoạn đường AB ngắn hơn đoạn đường CD 2km. Xác định chiều dài của mỗi đoạn đường, biết rằng chiều dài của đoạn AB bằng 3/4 chiều dài đoạn CD.
Tóm tắt:
Hướng dẫn giải và tính toán:
- Bước 1: Dựa vào sơ đồ, chúng ta tính hiệu số phần bằng nhau bằng cách lấy số phần của số lớn (4 phần) trừ số phần của số bé (3 phần), kết quả là 1 phần.
- Bước 2: Để tìm chiều dài đoạn đường AB, ta sử dụng giá trị hiệu số phần đã tính và nhân với chiều dài của đoạn AB, là 3 km. Kết quả là 1 phần nhân với 3 km, tương đương 3 km.
- Bước 3: Để xác định chiều dài đoạn đường CD, ta cộng chiều dài đoạn AB (3 km) với chiều dài đoạn CD, là 6 km. Kết quả là 3 km cộng với 6 km, tổng cộng 9 km.
Kết quả cuối cùng:
Chiều dài đoạn đường AB là 3 km.
Chiều dài đoạn đường CD là 9 km.
Tham khảo thêm nội dung chi tiết tại: Giải bài tập Toán lớp 4, bài 134: Tìm hiểu về diện tích hình thoi. Cảm ơn bạn!
