1. Bài tập Toán lớp 5 bài 69: Luyện tập
Câu 1: Thực hiện phép tính và ghi kết quả
864 : 2,4
9 chia cho 0,25
108 chia cho 22,5
Phương pháp giải quyết:
Để chia một số nguyên cho một số thập phân, thực hiện theo các bước sau:
- Xác định số chữ số thập phân trong số chia và thêm số lượng chữ số 0 tương ứng vào bên phải số bị chia
- Loại bỏ dấu phẩy trong số chia và thực hiện phép chia như với các số nguyên
Kết quả:
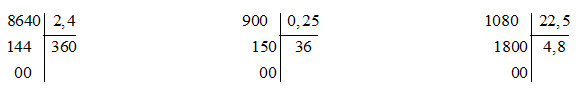
Câu 2: Tìm giá trị của X
a. X nhân với 4,5 = 72
b. 15 chia X = 0,85 cộng 0,35
Hướng dẫn giải:
- Tính giá trị của biểu thức bên phải (nếu cần thiết)
- Để tìm thừa số chưa biết, lấy tích chia cho thừa số đã biết
Kết quả:
a. X nhân 4,5 = 72
X = 72 chia 4,5
X = 16
b. 15 chia X = 0,85 cộng 0,35
15 chia X = 1,2
X = 1,2 chia 15
X = 12,5
Câu 3: Một mảnh đất hình chữ nhật có chiều rộng 7,2 m và diện tích bằng diện tích của sân hình vuông có cạnh 12m. Tính chiều dài của mảnh đất hình chữ nhật.
Tóm tắt:
Chiều rộng: 7,2 m
Diện tích của hình chữ nhật tương đương với diện tích của hình vuông có cạnh 12m
Chiều dài: ? m
Hướng dẫn giải:
- Tính diện tích hình vuông bằng cách nhân cạnh với chính nó
- Vì diện tích hình chữ nhật bằng diện tích của hình vuông có cạnh 12m, nên chúng ta có thể xác định diện tích hình chữ nhật từ đó
- Chiều dài của hình chữ nhật = diện tích chia cho chiều rộng
Kết quả:
Diện tích của sân hình vuông hay mảnh vườn hình chữ nhật là:
12 x 12 = 144 m²
Chiều dài của mảnh đất hình chữ nhật là:
144 chia 7,2 = 20 m
Kết quả: 20 m
Câu 4: Xác định ba giá trị của x sao cho: 5,5 < x < 5,52
Hướng dẫn giải:
Sử dụng phương pháp so sánh các số thập phân:
- Để so sánh hai số, trước tiên hãy so sánh phần nguyên của chúng như so sánh hai số tự nhiên. Số nào có phần nguyên lớn hơn thì số đó lớn hơn.
- Nếu phần nguyên của hai số bằng nhau, ta sẽ so sánh phần thập phân theo từng hàng từ hàng phần mười, phần trăm, phần nghìn,... Số nào có chữ số lớn hơn ở hàng tương ứng thì số đó lớn hơn.
- Nếu cả phần nguyên và phần thập phân của hai số đều giống nhau, thì hai số đó là bằng nhau.
Đáp án:
Tìm ba giá trị của x sao cho: 5,5 < x < 5,52
Các giá trị phù hợp là:
x = 5,501; 5,502; 5,503
Hoặc có thể giải theo cách khác:
Ta có: 5,5 < x < 5,52
5,50 < x < 5,52
x thuộc tập hợp { 5,51; 5,512; 5,513; ...}
Vì vậy, ba giá trị của x là: 5,51; 5,512; 5,513
2. Những kiến thức cần nhớ
Chia một số nguyên cho một số thập phân
Quy tắc: Để thực hiện phép chia một số nguyên cho một số thập phân, ta thực hiện theo các bước sau:
- Đếm số chữ số trong phần thập phân của số chia, sau đó thêm vào bên phải số chia số lượng chữ số 0 tương ứng.
- Loại bỏ dấu phẩy khỏi số chia, rồi thực hiện phép chia như với các số nguyên.
Ví dụ: Một mảnh vườn hình chữ nhật có diện tích 57 m² và chiều dài 9,5 m. Tìm chiều rộng của mảnh vườn.
Thực hiện phép chia:
57 : 9,5 = ? m
Ta có: 57 : 9,5 = (57 x 10) : (9,5 x 10)
57 : 9,5 = 570 : 95
Thông thường, ta đặt tính và thực hiện như sau:

Số 9,5 có một chữ số ở phần thập phân
Thêm một số 0 vào phía sau 57 thành 570; loại bỏ dấu phẩy trong số 9,5 để được 95
Thực hiện phép chia 570 chia cho 95
Vậy kết quả của 5,6 chia cho 9,5 là 6 m
Ví dụ 2:
99 chia cho 8,25 bằng bao nhiêu?
.jpg)
Số thập phân của 8,25 có hai chữ số
Thêm hai chữ số 0 vào sau số 99 để được 9900 và bỏ dấu phẩy trong 8,25 thành 825
Thực hiện phép chia 9900 cho 825
Để chia một số tự nhiên cho một số thập phân, làm theo các bước sau:
- Đếm số chữ số thập phân trong số chia, sau đó thêm cùng số lượng chữ số 0 vào phía sau số bị chia
Loại bỏ dấu phẩy trong số chia và thực hiện phép chia như với các số tự nhiên
- Các dạng bài tập liên quan bao gồm:
Dạng 1: Bài toán đơn giản về số thập phân
Phương pháp giải quyết:
- Đối với loại bài toán này, chúng ta thực hiện các bước giải giống như khi giải các bài toán liên quan đến số tự nhiên
- Chúng ta chỉ cần thực hiện các phép toán cộng, trừ, nhân, chia với số thập phân để tìm kết quả
Ví dụ 1: Mỗi bộ quần áo cần 2,8 mét vải. Tính số mét vải cần để may 20 bộ quần áo?
Số mét vải cần để may 20 bộ quần áo là:
2,8 x 20 = 56 m
Kết quả: 56 mét vải
Dạng 2: Bài toán tổng hợp về số thập phân
Phương pháp giải quyết:
- Đối với loại bài toán này, chúng ta thực hiện các bước giải tương tự như với bài toán số tự nhiên
- Tuy nhiên, cần thực hiện nhiều bước hơn để tìm ra kết quả so với bài toán đơn giản hơn
Ví dụ 1: Nếu 5,2 lít dầu có trọng lượng 3,952 kg, hỏi cần bao nhiêu lít dầu để đạt trọng lượng 5,32 kg?
Trọng lượng của một lít dầu là:
3,952 chia cho 5,2 = 0,76 kg
Với trọng lượng 5,32 kg, số lít dầu cần có là:
5,32 chia cho 0,76 = 7 lít
Kết quả: 7 lít
3. Các bài toán vận dụng để tự luyện tập
Câu 1: Một thùng chứa 31,2 kg đường. Sau khi lấy ra 10,2 kg ở lần đầu và 12,7 kg ở lần sau, thùng còn lại bao nhiêu kg đường?
Câu 2: Một người đi xe đạp, trong 3 giờ đầu di chuyển được 10,5 km mỗi giờ, và trong 4 giờ tiếp theo đi được 9,45 km mỗi giờ. Tổng quãng đường đã đi là bao nhiêu km?
Câu 3: Một cửa hàng bán 25,6 m vải cho ba người. Người thứ nhất mua 3,5 m vải, người thứ hai mua nhiều hơn người thứ nhất 1,8 m. Người thứ ba mua được bao nhiêu mét vải?
Câu 4: Có ba tổ công nhân tham gia vào việc đắp đường. Tổ một và tổ hai đã đắp tổng cộng 23,4 m đường, tổ hai và tổ ba đã đắp được 20,5 m đường, và tổng cộng cả ba tổ đã đắp được 36,2 m đường. Tính số mét đường mà mỗi tổ đã đắp được.
Câu 5: Một cửa hàng có ba thùng dầu. Thùng đầu tiên chứa 9,7 lít dầu, thùng thứ hai nhiều hơn thùng đầu tiên 3,5 lít. Sau khi bán 16,3 lít dầu, cửa hàng còn lại 22,2 lít dầu. Hãy tính lượng dầu trong thùng thứ ba.
Câu 6: Có hai bao gạo, bao thứ nhất nặng gấp ba lần bao thứ hai. Nếu thêm vào bao gạo thứ nhất 6,4 kg, thì bao gạo thứ nhất sẽ nặng hơn bao gạo thứ hai 18,8 kg. Tính trọng lượng của từng bao gạo.
Câu 7: Một cửa hàng bán đường có một số lượng đường nhất định. Ngày đầu tiên cửa hàng bán 9,5 tạ đường và số còn lại được chia đều thành 18 bao. Ngày hôm sau, cửa hàng bán 12 bao và còn lại 3,12 tạ đường. Tính tổng số tạ đường của cửa hàng trước khi bán.
Câu 8: Ba tổ công nhân tham gia đắp đường với các số liệu như sau: tổ một và tổ hai đắp tổng cộng 23,4 m đường, tổ hai và tổ ba đắp được 20,5 m đường, và ba tổ cùng đắp được 36,2 m đường. Xác định số mét đường mà mỗi tổ đã đắp.
Câu 9: Một cửa hàng có ba thùng dầu, trong đó thùng đầu tiên chứa 9,7 lít dầu và thùng thứ hai nhiều hơn thùng đầu tiên 3,5 lít. Sau khi bán 16,3 lít dầu, cửa hàng còn lại 22,2 lít dầu. Tính lượng dầu trong thùng thứ ba.
Câu 10: Bao gạo đầu tiên nặng gấp ba lần bao gạo thứ hai. Nếu thêm vào bao gạo đầu tiên 6,4 kg, thì bao gạo đầu tiên sẽ nặng hơn bao gạo thứ hai 18,8 kg. Xác định trọng lượng của mỗi bao gạo.
