1. Bất phương trình là gì?
Bất phương trình một ẩn là một mệnh đề so sánh hai hàm số f(x) và g(x) trên tập số thực dưới một trong các dạng sau:
f(x) < g(x)
f(x) > g(x)
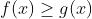
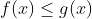
2. Phương pháp giải bất phương trình bậc nhất một ẩn
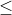
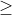
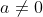
Giải bất phương trình ax + b > 0 (1)
Bất phương trình (1) tương đương với ax > -b
Nếu a > 0 thì (1) tương đương với x > -b/a
3. Bất phương trình bậc hai với một ẩn
222 2
2
Giải bất phương trình bậc hai ax2 + bx + c < 0 thực chất là xác định các khoảng mà trong đó f(x) = ax2 + bx + c < 0 có cùng dấu với hệ số a (khi a < 0) hoặc trái dấu với hệ số a (khi a > 0)
4. Tập nghiệm của bất phương trình
Số x = 0 được gọi là nghiệm của một bất phương trình nếu khi thay x = 0 vào bất phương trình, ta nhận được một bất đẳng thức đúng
Tập nghiệm của bất phương trình là tập hợp tất cả các giá trị x thỏa mãn bất phương trình đó.
Hai bất phương trình được coi là tương đương nếu chúng có cùng tập nghiệm.
5. Những quy tắc quan trọng cần nhớ:
- Quy tắc chuyển vế: Khi chuyển một hạng tử từ vế này sang vế kia của bất phương trình, phải đổi dấu của hạng tử đó.
- Quy tắc nhân với một số: Khi nhân cả hai vế của bất phương trình với cùng một số khác không, ta phải:
Giữ nguyên chiều của bất phương trình nếu số nhân là dương
Đổi chiều của bất phương trình nếu số nhân là âm
BÀI TẬP LUYỆN TẬP
Các dạng toán giải bất phương trình:
Dạng 1: Xác định nghiệm hoặc tập nghiệm của một bất phương trình và biểu diễn nghiệm hoặc tập nghiệm đó trên trục số
Dạng 2: Xác định hai bất phương trình tương đương
Dạng 3: Giải bất phương trình bậc hai
Dạng 4: Giải bất phương trình tích
Dạng 5: Giải bất phương trình có ẩn ở mẫu
Dạng 6: Tìm điều kiện của tham số để bất phương trình vô nghiệm, có nghiệm hoặc nghiệm đúng
Dạng 7: Giải hệ bất phương trình bậc hai
Bài 1: Giải bất phương trình -6x + 12 < 0
Hướng dẫn giải:
-6x + 12 < 0 ⇔ -6x < 12 ⇔ x > 2
Do đó, tập nghiệm của bất phương trình là S = {x | x > 2}
Bài 2: Giải bất phương trình -5x + 15 > 0
Hướng dẫn giải: -5x + 15 > 0 ⇔ -5x < -15 ⇔ x < 3
Vậy tập nghiệm của bất phương trình là S = {x | x < 3}
a, x - 4 > 4
B, 2x > x + 2
C, 2x - 2 < 3x - 2
D, 2 - 2x < -x - 3
E, 4x - 5 > 2(x - 1) + x
Lời giải:
A, Có x - 4 > 4 ⇔ x > 8
Do đó, tập nghiệm của bất phương trình là S = { x | x > 8}
B, Có 2x > x + 2 ⇔ x > 2
Vậy phương trình có tập nghiệm S = { x | x > 2}
C, Có 2x - 2 < 3x - 2 ⇔ 0 < x
Vậy tập nghiệm của bất phương trình là S = {x | x > 0}
D. Có 3 - 2x < -x - 3 ⇔ -2x + x < -6 ⇔ x < -6
Do đó, tập nghiệm của bất phương trình là S = { x | x < -6}
E. Có 4x - 5 > 2(x - 1) + x ⇔ 4x - 5 > 2x - 2 + x ⇔ 2x > 3 ⇔ x > 3/2
Vậy tập nghiệm của bất phương trình là S = { x | x > 3/2}
Bài 3: Tìm tập nghiệm S của bất phương trình 5x - 1 > (2x/5) + 3
A. S = R
B. x > 2
C. x > 5/2
D. x > 20/23
Đáp án: Chọn D. Bất phương trình có tập nghiệm S = {x | x > 20/23}
Bài 4: Bất phương trình [(3x + 5) / 2] - 1 < [(x + 2) / 3 + x] có bao nhiêu nghiệm nguyên lớn hơn 10?
A. 4 nghiệm nguyên lớn hơn 10
B. 5 nghiệm nguyên lớn hơn 10
C. 6 nghiệm nguyên lớn hơn 10
D. Có 7 nghiệm nguyên lớn hơn 10
Đáp án: Chọn B. Bất phương trình có 4 nghiệm nguyên lớn hơn 10.
Bài 5: Tìm giá trị m để x = 2 là nghiệm của bất phương trình mx + 2 < x + 3 + m
A. m = 2
B. m < 3
C. m > 1
D. m < -3
Đáp án: Chọn B. Để x = 2 là nghiệm của bất phương trình, m cần thỏa mãn m < 3
Bài 6: Những bất phương trình nào là bất phương trình một ẩn?
A. 2x - 3 < 0
B. 5 > 0
C. 5x - 5 > 0
D. x2 + 3 > 0
Đáp án: Các phương trình một ẩn bao gồm phương trình A và phương trình C.
Bài 7: Nghiệm x = 3 thuộc vào bất phương trình nào trong số những bất phương trình sau đây?
A. 6 - x < 1
B. 3x + 2 < 3
C. 4x - 10 > x
D. 2x - 1 > 3
Hướng dẫn giải: Chọn đáp án D. x = 3 là nghiệm của bất phương trình 2x - 1 > 3
Chúng ta có:
A. 6 - x < 1 ⇔ x > 5
B. 3x + 2 < 3 ⇔ 3x < 1 ⇔ x < 1/3
C. 4x - 10 > x ⇔ 3x > 10 ⇔ x > 10/3
D. 2x - 1 > 3 ⇔ 2x > 4 ⇔ x > 2
Bài 8: Xét bất phương trình x - 2 > 0. Trong các bất phương trình dưới đây, bất phương trình nào tương đương với bất phương trình đã cho?
A. 2x - 4 < 0
B. x - 4 > 0
C. 3x - 6 > 0
D. 1 - 3x < 3
Giải thích:
Chúng ta có: x - 2 > 0 tương đương với x > 2
A. 2x - 4 < 0 tương đương với x < 2
B. x - 4 > 0 tương đương với x > 4
C. 3x - 6 > 0 tương đương với 3x > 6 tương đương với x > 2
D. 1 - 3x < 3 tương đương với -3x < 2 tương đương với x > 2/3
Vậy bất phương trình 3x - 6 > 0 tương đương với bất phương trình x - 2 > 0
Bài 9: Lập bất phương trình cho bài toán sau:
Cô Mai chia đều 10 cái kẹo cho 2 bạn nhỏ. Hỏi mỗi bạn nhận bao nhiêu cái kẹo để cô Mai vẫn còn kẹo sau khi chia?
A. 2x < 10
B. 2x > 10
C. 10x < 2
D. 10x > 2
Trong đó, x là số kẹo mà mỗi bạn nhận được
Giải: Chọn đáp án A.
Gọi số kẹo mỗi bạn nhận được là x (cái kẹo)
Như vậy, tổng số kẹo của 2 bạn là 2x
Để sau khi chia xong còn kẹo, điều kiện là 2x < 10
Bài 10: Bạn Oanh có 15000 đồng, muốn mua x quyển vở và 1 cái bút giá 4000 đồng. Mỗi quyển vở giá 3000 đồng. Lập phương trình với ẩn x.
A. 4000 + 3000.x < 15000
B. 4000 + 3000x > 15000
C. 3000x < 15000
D. Tất cả các đáp án đều sai
Giải: Chọn đáp án B
Chi phí cho x quyển vở là 3000x (đồng)
Tổng chi phí cho 1 cây bút và x quyển vở là 4000 + 3000x (đồng)
Vì bạn Oanh có 15000 đồng, nên ta thiết lập bất phương trình: 4000 + 3000x < 15000
Bài 11: Kết luận nào sau đây đúng về nghiệm của bất phương trình (x + 4)(x + 4) > (x - 1)(x + 9) + 25
A. Bất phương trình vô nghiệm
B. Bất phương trình có vô số nghiệm
C. Bất phương trình có tập nghiệm S = {x > 0}
D. Bất phương trình có tập nghiệm S = {x < 0}
Lời giải: Chọn đáp án B
Ta có (x + 4)(x + 4) > (x - 2)(x + 10) + 25
<= x2 + 8x + 16 > x2 + 8x - 20 + 25
<= x2 + 8x + 16 - x2 - 8x + 20 - 25 > 0
<= 11 > 0
Vì 11 > 0 luôn đúng nên bất phương trình có vô số nghiệm.
Đây là bài viết của Mytour trả lời cho câu hỏi Cách giải bất phương trình dễ hiểu nhất, hy vọng bài viết này sẽ giúp bạn nắm vững kiến thức về bất phương trình.
