1. Kiến thức cơ bản về phương trình trùng phương
Phương trình trùng phương là một loại phương trình bậc bốn với các hệ số đứng trước x2 và x bằng 0. Theo định nghĩa, đây là phương trình có dạng:
ax4 + bx2 + c = 0 với a khác 0.
2. Phương pháp giải phương trình trùng phương
Hướng dẫn giải phương trình trùng phương:42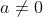 2
2 2
2
Bước 2: Giải phương trình bậc hai theo ẩn t
Bước 3: Giải phương trình x² = t để tìm nghiệm
Bước 4: Đưa ra kết luận
Xem xét số lượng nghiệm của phương trình trùng phương
- Nếu phương trình (1) có bốn nghiệm phân biệt, thì phương trình (2) sẽ có hai nghiệm dương phân biệt
- Nếu phương trình (1) có ba nghiệm phân biệt, thì phương trình (2) sẽ có một nghiệm dương và một nghiệm t = 0
- Nếu phương trình (1) có hai nghiệm phân biệt, thì phương trình (2) sẽ có hai nghiệm trái dấu hoặc một nghiệm kép dương
- Nếu phương trình (1) chỉ có một nghiệm duy nhất, thì phương trình (2) sẽ có nghiệm kép x = 0 hoặc một nghiệm x = 0 và một nghiệm âm
- Nếu phương trình (1) không có nghiệm, thì phương trình (2) cũng không có nghiệm hoặc có hai nghiệm âm
* Số nghiệm của phương trình trùng phương có dạng
ax⁴ + bX² + c = 0

Khi đó:
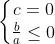
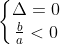

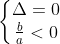

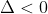

3. Bài tập thực hành
Bài 1: Tìm giá trị của m để phương trình x4 + 2mx2 + 8 = 0 có bốn nghiệm phân biệt sao cho tổng của bình phương các nghiệm bằng 32
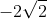
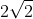
C. m = -8
D. m = 8
Giải đáp: Đáp án đúng là C
Gọi phương trình x4 + 2mx2 + 8 = 0 là (1)
2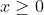
t2 + 2mt + 8 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt ⇔ phương trình (2) có hai nghiệm dương phân biệt

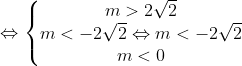
Gọi x1, x2, x3, x4 là bốn nghiệm phân biệt của phương trình (1), và t1, t2 là hai nghiệm dương phân biệt của phương trình (2). Ta có:
 1212
1212Dựa vào bài toán, chúng ta có:
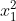
Do đó, m = -8
Bài 2: Điều kiện để các hệ số a và b sao cho phương trình x4 - 2x(a2 + b2)x2 + (a2 - b2)2 = 0 có ba nghiệm phân biệt là
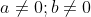
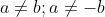
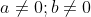
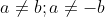
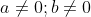
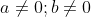
Bài 3: Giải các phương trình trùng phương:
a, x4 - 5x2 + 4 = 0
b, 2x4 - 3x2 - 2 = 0
c, 3x4 + 10x2 + 3 = 0
Giải pháp:
a, x4 - 5x2 + 4 = 0 (1)
2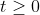
Vậy phương trình (1) trở thành t2 - 5t + 4 = 0 (2)
Giải phương trình (2) ta có: Với a = 1; b = -5; c = 4 => a + b + c = 0
=> Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4
Cả hai giá trị đều thỏa mãn điều kiện
+ Với t = 1 => x2 = 1 => x = 1 hoặc x = -1
+ Với t = 4 => x2 = 4 => x = 2 hoặc x = -2
Do đó, phương trình (1) có nghiệm S = {-2; -1; 1; 2}
b. 2x4 - 3x2 - 2 = 0 (1)
2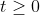 2
2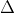 2
2=> Phương trình có hai nghiệm t1 = 2; t2 = -0,5
2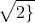
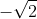
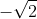
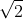
c, 3x4 + 10x2 + 3 = 0 (1)
12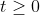 12
12Bài 4: Số nghiệm của phương trình 3x4 - 2x2 - 5 = 0 (1) là
A. 0
B. 1
C. 2
D. 4
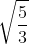
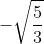
Bài 5: Số nghiệm âm của phương trình 3x4 + 10x2 + 3 = 0 là
A. 0
B. 4
C. 2
D. 3
Giải thích: Chọn đáp án A
2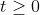 2
2 2
2Do đó, phương trình (2) có 2 nghiệm phân biệt
t = -1/3 < 0 (Loại)
t2 = -3 < 0 (Loại)
Vì vậy, phương trình (1) không có nghiệm âm, tức là phương trình (1) vô nghiệm
Bài 6: Số nghiệm của phương trình -15x4 - 26x2 + 10 = 0 là
A. 1 nghiệm
B. 2 nghiệm
C. 3 nghiệm
D. 4 nghiệm
Lời giải: Phương trình có 2 nghiệm phân biệt, trong đó t1 < 0 (loại) và t2 > 0 (hợp lệ). Do đó, phương trình có 2 nghiệm.
Bài 7: Tìm giá trị của m để phương trình (m + 1)4 + 5x2 - m - 1 = 0 có chính xác hai nghiệm phân biệt.
A. -1 < m < 1 và m khác 0
B. -1 < m < 1
C. -1 < m < 2
D. Không có giá trị m nào thỏa mãn
Giải: Lựa chọn đáp án D
- Trường hợp 1: Khi m = -1, phương trình (1) trở thành phương trình bậc 2 5x2 = 0 ⟹ x2 = 0 ⟹ x = 0.
Phương trình chỉ có một nghiệm nên m = -1 không phù hợp.
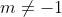 2
2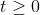 2
2Phương trình (1) có đúng 2 nghiệm trái dấu hoặc nghiệm kép dương
Tình huống phương trình (2) có nghiệm kép dương không xảy ra với mọi m.
- Phương trình (2) có hai nghiệm trái dấu: (m + 1)(-m -1) < 0 ⟹ (m + 1)2 < 0, không có m nào thỏa mãn.
Do đó, không tồn tại giá trị nào của m đáp ứng yêu cầu bài toán.
Bài 8: Xét phương trình m2x4 + x2 - m2 - 1 = 0 với m là tham số. Chọn khẳng định không đúng
A. Phương trình luôn có hai nghiệm phân biệt với mọi m khác 0
B. Phương trình luôn có hai nghiệm phân biệt với m khác 0
C. x = -1 và x = 1 đều là nghiệm của phương trình
D. X=2 không phải là nghiệm của phương trình
Giải thích: Chọn đáp án A. Phương trình luôn có nghiệm phân biệt với mọi m khác 0
- Trường hợp 1: m = 0, phương trình (1) trở thành phương trình bậc hai ⇔ x = 1 và x = -1
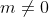
Bài 9: Các nghiệm của phương trình x4 + 5x2 - 6 = 0 là
A. x = -2
B. x = 3
C. x = 2 hoặc x = -3
D. Phương trình không có nghiệm
Bài 10: Số nghiệm của phương trình (x +1)4 - 5(x + 1)2 - 84 = 0 là
A. Phương trình không có nghiệm
B. Phương trình có một nghiệm
C. Phương trình có hai nghiệm
D. Phương trình có bốn nghiệm
2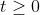 2
2 2
2Phương trình (2) có hai nghiệm phân biệt: t1 = -7 (không hợp lệ), t2 = 12 (hợp lệ)
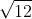
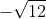
Trên đây là bài viết của Luật Mytour giải đáp câu hỏi về cách giải bài tập phương trình trùng phương. Hy vọng những kiến thức này sẽ giúp bạn đọc hiểu rõ và nắm vững kiến thức về phương trình trùng phương, cũng như áp dụng hiệu quả vào các bài tập. Xin chân thành cảm ơn!
