Hướng dẫn giải Toán 9 Bài 8: Phương pháp lập phương trình dễ hiểu

Buzz

Nội dung bài viết

Bài 41 trang 58 SGK Toán 9 Tập 2

Bài 42 (trang 58 SGK Toán 9 Tập 2)

Bài 43 trang 58 SGK Toán 9 Tập 2

Bài 44 (trang 58 SGK Toán 9 Tập 2)

Bài 45 (trang 59 SGK Toán 9 Tập 2)

Bài 46 (trang 59 SGK Toán 9 Tập 2)

Bài 47 (trang 59 SGK Toán 9 Tập 2)

Bài 48 (trang 59 SGK Toán 9 Tập 2)

Bài 49 (trang 59 SGK Toán 9 Tập 2)

Bài 50 (trang 59 SGK Toán 9 Tập 2)

Bài 51 (trang 59 SGK Toán 9 Tập 2)

Bài 52 (trang 60 SGK Toán 9 Tập 2)

Bài 53 (trang 60 SGK Toán 9 Tập 2)

Xem thêm

Với lời giải chi tiết cho SBT Toán 9 Bài 8: Phương pháp lập phương trình hiệu quả, học sinh lớp 9 sẽ hoàn thành bài tập trong sách một cách dễ dàng.

Bài 41 trang 58 SGK Toán 9 Tập 2

Trong buổi học nhóm, bạn Hùng yêu cầu Minh và Lan chọn hai số sao cho chúng cách nhau 5 đơn vị và tích của chúng là 150. Vậy hai số đó là gì?

Giải chi tiết

Gọi x là số mà một bạn đã chọn

⇒ Số còn lại sẽ là x + 5.

⇒ Tích của hai số là x(x+5).

Theo bài toán, ta thiết lập phương trình:

x(x + 5) = 150

$x^{2}$ $x^{2}$

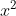
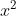
Phương trình (*) có: a = 1; b = 5; c = -150

⇒ Δ = 5^{2} - 4.1.(-150) = 625 > 0

⇒ Phương trình (*) có hai nghiệm

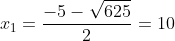
${x_1}= \dfrac{{ - 5 + \sqrt {625} }}{2}=10,$ ${x_1}= \dfrac{{ - 5 - \sqrt {625} }}{2}= -15$

Vậy hai số Minh và Lan cần chọn là 10 và 15.

Hoặc hai số các bạn chọn là -10 và -15.

Bài 42 (trang 58 SGK Toán 9 Tập 2)

Bác Thời vay 2.000.000 đồng từ ngân hàng để phát triển kinh tế gia đình trong vòng một năm. Dự kiến, cuối năm bác sẽ phải hoàn trả cả vốn và lãi. Tuy nhiên, ngân hàng đã đồng ý kéo dài thời gian thêm một năm nữa, số lãi năm đầu sẽ được cộng vào vốn để tính lãi cho năm sau và lãi suất không thay đổi. Sau hai năm, tổng số tiền bác phải trả là 2.420.000 đồng. Tính lãi suất cho vay hàng năm là bao nhiêu phần trăm?

Hướng dẫn giải:

Gọi lãi suất cho vay hàng năm là x (%), với x > 0.

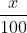
$\dfrac{x}{100}$

Sau 1 năm, tổng số tiền bao gồm cả vốn và lãi là: 2.000.000 + 20.000x (đồng)

Lãi suất phải trả riêng trong năm thứ hai là:

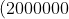
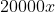
$(2.000.000 + 20.000x) \dfrac{x}{100}$ $20.000x + 200x^{2}$

Tổng số tiền bác Thời phải thanh toán sau hai năm là:

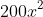
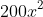
$200x^{2}$ $200x^{2}$

Dựa vào đề bài, ta thiết lập phương trình:

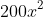
$200x^{2}$ $x^{2}$

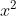
Giải phương trình trên:

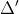
$\Delta'$ $100^{2}$

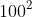
= 10.000 + 2.100 = 12.100 > 0

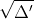
$\sqrt{\Delta'}$ ${x_1}=\dfrac{-100-110}{1} = -210, {x_2}=\dfrac{-100+110}{1}$ ${x_1}$

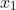
Lãi suất hàng năm là 10%.

Bài 43 trang 58 SGK Toán 9 Tập 2

Một xuồng du lịch di chuyển từ thành phố Cà Mau đến Đất Mũi theo một con đường sông dài 120km. Trên đường đi, xuồng dừng lại 1 giờ tại thị trấn Năm Căn. Khi trở về, xuồng đi theo con đường khác dài hơn 5km và với vận tốc chậm hơn 5km/h so với lúc đi. Tính vận tốc của xuồng lúc đi, biết rằng thời gian đi và thời gian về là như nhau.

Hướng dẫn giải:

Gọi vận tốc của xuồng khi đi là x (km/h), thì vận tốc khi về sẽ là x - 5 (km/h), với x > 5.

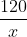
$\dfrac{120}{x}$

Quãng đường về dài: 120 + 5 = 125 (km)

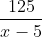
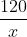
$\dfrac{125}{x-5}$ $\dfrac{120}{x} + 1 = \dfrac{125}{x-5}$

Giải phương trình sau:

$x^2 - 5x + 120x - 600 = 125x \Leftrightarrow x^2 - 10x - 600 = 0$

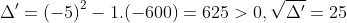
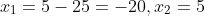
${x_1} = \dfrac{10 - 25}{2} = -20, {x_2} = \dfrac{10 + 25}{2} = 30$ ${x_1}$

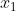
Vận tốc của xuồng khi đi là 30 km/h.

Bài 44 (trang 58 SGK Toán 9 Tập 2)

Tìm một số sao cho một nửa của nó trừ đi một nửa đơn vị rồi nhân với một nửa của nó bằng một nửa đơn vị.

Hướng dẫn giải:

Gọi số cần tìm là x.

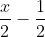
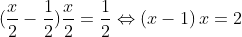
$\dfrac{x}{2} - \dfrac{1}{2}$ $\left( \dfrac{x}{2} - \dfrac{1}{2} \right) \dfrac{x}{2} = \dfrac{1}{2} \Leftrightarrow (x - 1)x = 2$

Hay x^2 - x - 2 = 0, với a - b + c = 1 - (-1) - 2 = 0, nên phương trình có hai nghiệm là: x_1 = -1 và x_2 = 2

Vậy số cần tìm là -1 hoặc 2.

Bài 45 (trang 59 SGK Toán 9 Tập 2)

Tích của hai số nguyên dương liên tiếp vượt quá tổng của chúng là 109. Tìm hai số đó.

Hướng dẫn giải:

Gọi hai số nguyên dương liên tiếp cần tìm là x và x + 1 (x ∈ N).

Tích của hai số là: x(x + 1) = x^2 + x.

Tổng của hai số là: x + (x + 1) = 2x + 1.

Theo đề bài, ta có phương trình: x^2 + x = 2x + 1 + 109

⇔ x^2 – x – 110 = 0

Với a = 1; b = -1; c = -110, ta có Δ = (-1)^2 – 4.1.(-110) = 441.

⇒ Phương trình có hai nghiệm là:

${x_1} = \dfrac{-(-1) + \sqrt{441}}{2} = 11, {x_2} = \dfrac{-(-1) - \sqrt{441}}{2} = -10$

Trong hai nghiệm, chỉ có nghiệm x = 11 phù hợp với yêu cầu.

Do đó, hai số tự nhiên cần tìm là 11 và 12.

Bài 46 (trang 59 SGK Toán 9 Tập 2)

Một mảnh đất hình chữ nhật có diện tích 240 m². Nếu ta tăng chiều rộng thêm 3m và giảm chiều dài đi 4m, thì diện tích của mảnh đất vẫn giữ nguyên. Tính kích thước của mảnh đất.

Hướng dẫn giải:

Gọi chiều rộng của mảnh đất là x (m), với x > 0.

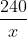
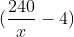
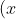
$Chiều dài của mảnh đất là \dfrac{240}{x}.$ $Khi chiều rộng tăng thêm 3m và chiều dài giảm đi 4m, chiều dài mới sẽ là (\dfrac{240}{x} - 4).$ $Diện tích mới của mảnh đất sẽ là (x + 3)\left(\dfrac{240}{x} - 4\right) = 240 - 4x + \dfrac{720}{x} - 12 (m^2).$

Ta có phương trình từ bài toán như sau:

$\begin{array}{l} 240 - 4x + \dfrac{720}{x} - 12 = 240\\ \Rightarrow -4x^2 + 720 - 12x = 0\\ \Leftrightarrow x^2 + 3x - 180 = 0 \end{array}$ $\Delta = 3^2 + 4 \cdot 180 = 729, \sqrt{\Delta} = 27$ $Nghiệm phương trình: {x_1} = \dfrac{-3 + 27}{2} = 12, {x_2} = \dfrac{-3 - 27}{2} = -15.$

Vì x phải dương, nên x = -15 không hợp lệ. Do đó, chiều rộng là 12m và chiều dài là: 240 : 12 = 20 (m).

Kết luận, mảnh đất có chiều rộng 12m và chiều dài 20m.

Bài 47 (trang 59 SGK Toán 9 Tập 2)

Bác Hiệp và cô Liên cùng khởi hành từ làng đến tỉnh trên quãng đường dài 30km. Bác Hiệp đi nhanh hơn cô Liên 3km/h, vì vậy bác Hiệp đến nơi sớm hơn cô Liên nửa giờ. Xác định vận tốc của mỗi người.

Hướng dẫn giải:

Đặt vận tốc của bác Hiệp là x (km/h). Vậy vận tốc của cô Liên là x - 3 (km/h), với x > 3.

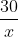
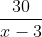
$Thời gian đi của bác Hiệp là \dfrac{30}{x} giờ.$ $Thời gian đi của cô Liên là \dfrac{30}{x-3} giờ.$

Vì bác Hiệp đến trước cô Liên nửa giờ, tức là thời gian đi của bác Hiệp ngắn hơn thời gian của cô Liên nửa giờ, ta thiết lập phương trình:

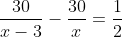
$\dfrac{30}{x-3} - \dfrac{30}{x} = \dfrac{1}{2}$

Giải phương trình:

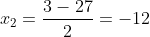
$Nghiệm x_1 = \dfrac{3 + 27}{2} = 15$ $Nghiệm x_2 = \dfrac{3 - 27}{2} = -12$

Vì vận tốc phải lớn hơn 3 km/h nên nghiệm x_2 = -12 không phù hợp.

Do đó, vận tốc của bác Hiệp là 15 km/h

Vận tốc của cô Liên là 12 km/h

Bài 48 (trang 59 SGK Toán 9 Tập 2)

Một miếng tôn hình chữ nhật có bốn góc bị cắt đi bốn hình vuông với cạnh 5dm để tạo thành một cái thùng hình hộp chữ nhật không có nắp với thể tích 1500dm³ (h.15). Tính kích thước ban đầu của miếng tôn, biết rằng chiều dài gấp đôi chiều rộng.

Hướng dẫn giải:

Gọi chiều rộng của miếng tôn là x (dm), với x > 10.

Chiều dài của miếng tôn là 2x (dm)

Khi tạo thành thùng hình hộp chữ nhật không có nắp, chiều dài của thùng là 2x - 10 (dm), chiều rộng là x - 10 (dm), và chiều cao là 5 (dm).

Thể tích của thùng được tính bằng công thức 5(2x - 10)(x - 10) (dm³).

Theo đề bài, ta có phương trình:

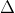
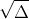
$\begin{array}{l} 5\left( {2x - 10} \right)\left( {x - 10} \right) = 1500\\ \Leftrightarrow 5\left( {2{x^2} - 20x - 10x + 100} \right) = 1500\\ \Leftrightarrow 2{x^2} - 30x + 100 = 300\\ \Leftrightarrow {x^2} - 15x - 100 = 0 \end{array}$ $\Delta$ $\sqrt{\Delta}$

Từ đó, ta có nghiệm x1 = 20 và x2 = -5 (loại bỏ).

Do đó, kích thước miếng tôn là chiều rộng 20 dm và chiều dài 40 dm.

Bài 49 (trang 59 SGK Toán 9 Tập 2)

Hai đội thợ quét sơn một ngôi nhà. Nếu làm chung thì họ hoàn tất trong 4 ngày. Nếu làm riêng, đội I hoàn thành sớm hơn đội II 6 ngày. Tính số ngày mỗi đội cần để hoàn thành công việc một mình.

Hướng dẫn giải:

Gọi số ngày đội I cần để hoàn thành công việc một mình là x (ngày), với x > 0.

Do đội II mất thêm 6 ngày so với đội I, nên thời gian để đội II hoàn thành công việc một mình là x + 6 (ngày).

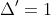
$\dfrac{1}{x}$ $\dfrac{1}{x+6}$ $\dfrac{1}{4}$ $\dfrac{1}{x} + \dfrac{1}{x+6} = \dfrac{1}{4}$ $\begin{array}{l} \Rightarrow 4\left( {x + 6} \right) + 4x = x\left( {x + 6} \right)\\ \Leftrightarrow 4x + 24 + 4x = {x^2} + 6x\\ \Leftrightarrow {x^2} - 2x - 24 = 0 \end{array}$ $\Delta' = 1 + 24 = 25 = 5^2$

Do đó, x1 = 1 + 5 = 6, x2 = 1 - 5 = -4

Vì x > 0 nên x2 = -4 không đáp ứng yêu cầu.

Do đó, đội I sẽ hoàn thành công việc trong 6 ngày khi làm một mình.

Đội II sẽ cần 12 ngày để hoàn thành công việc nếu làm một mình.

Bài 50 (trang 59 SGK Toán 9 Tập 2)

Miếng kim loại thứ nhất có khối lượng 880g, miếng thứ hai là 858g. Thể tích miếng thứ nhất kém thể tích miếng thứ hai 10cm³, và khối lượng riêng của miếng thứ nhất vượt khối lượng riêng của miếng thứ hai 1 g/cm³. Xác định khối lượng riêng của từng miếng kim loại.

Hướng dẫn giải:

Gọi khối lượng riêng của miếng kim loại đầu tiên là x (g/cm³).

Khối lượng riêng của miếng kim loại thứ hai là x - 1 (g/cm³), với điều kiện x > 1.

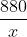
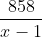
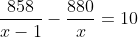
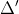
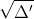
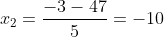
$\dfrac{880}{x}$ $\dfrac{858}{x-1}$ $\dfrac{858}{x-1} - \dfrac{880}{x} = 10$ $\begin{array}{l} \Rightarrow 858x - 880\left( {x - 1} \right) = 10x\left( {x - 1} \right)\\ \Leftrightarrow 858x - 880x + 880 = 10{x^2} - 10x\\ \Leftrightarrow 10{x^2} + 12x - 880 = 0\\ \Leftrightarrow 5{x^2} + 6x - 440 = 0 \end{array}$ $\Delta'$ $\sqrt{\Delta' }$ ${x_1} = \dfrac{{ - 3 + 47}}{5}= 8,8$ ${x_2} = \dfrac{{ - 3 - 47}}{5}= -10$

Vì x phải lớn hơn 1, nên x2 = -10 không hợp lệ

Khối lượng riêng của miếng kim loại thứ nhất là: 8,8 g/cm³

Khối lượng riêng của miếng kim loại thứ hai là: 7,8 g/cm³

Bài 51 (trang 59 SGK Toán 9 Tập 2)

Khi thêm 200g nước vào dung dịch chứa 40g muối, nồng độ của dung dịch giảm 10%. Tìm khối lượng nước có trong dung dịch trước khi thêm nước.

Hướng dẫn giải:

Đặt khối lượng nước trong dung dịch trước khi thêm nước là x (g), với x > 0.

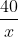
$\dfrac{40}{x + 40}$

Sau khi thêm 200 g nước, tổng khối lượng dung dịch là: x + 40 + 200 (g).

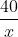
$\dfrac{40}{x + 40}$

Do nồng độ muối giảm 10%, ta thiết lập phương trình sau:

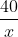
$\dfrac{40}{x + 40} - \dfrac{40}{x + 240} = \dfrac{10}{100}$

Giải phương trình như sau:

(x + 40)(x + 240) = 400(x + 240 - x - 40)

x^2 + 280x - 70400 = 0

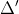
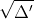
$\Delta'$ $\sqrt{\Delta'}$ ${x_1}$ ${x_2}$ ${x_2}$

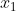
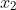
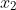
Trước khi thêm nước, dung dịch chứa 160 g nước.

Bài 52 (trang 60 SGK Toán 9 Tập 2)

Khoảng cách giữa hai bến sông A và B là 30 km. Một canô khởi hành từ bến A đến bến B, dừng lại 40 phút tại bến B rồi trở về bến A. Tổng thời gian từ lúc khởi hành đến khi về đến bến A là 6 giờ. Xác định vận tốc của canô trong nước yên lặng, biết rằng tốc độ dòng nước là 3 km/h.

Hướng dẫn giải:

Đặt vận tốc thực sự của canô là x (km/h), với x > 3.

Vận tốc của canô khi đi xuôi dòng là: x + 3 (km/h).

Vận tốc của canô khi đi ngược dòng là: x – 3 (km/h).

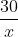
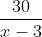
$\dfrac{30}{x + 3}$ $\dfrac{30}{x - 3}$ $\frac{2}{3}$

Tổng thời gian từ khi khởi hành đến khi về bến A là 6 giờ, do đó ta có:

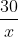
$\frac{30}{x + 3} + \frac{30}{x - 3} + \frac{2}{3} = 6$

⇔ 30 \cdot 3 \cdot (x - 3) + 30 \cdot 3 \cdot (x + 3) + 2 \cdot (x + 3) \cdot (x - 3) = 6 \cdot 3 \cdot (x + 3) \cdot (x - 3)

$x^{2}$ $x^{2}$ $x^{2}$ $x^{2}$ $x^{2}$ $x^{2}$ $x^{2}$

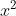
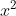
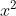
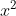
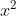
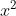
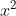
Với a = 4, b = -45, c = -36

$(-45)^{2}$

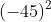
Phương trình có hai nghiệm là:

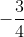
$-\frac{3}{4}$

Do đó, vận tốc của canô trong nước yên lặng là 12 km/h.

Bài 53 (trang 60 SGK Toán 9 Tập 2)

Hãy chia đoạn AB thành hai đoạn sao cho tỷ lệ giữa đoạn lớn và đoạn AB bằng tỷ lệ giữa đoạn nhỏ và đoạn lớn (h.16). Tìm tỷ lệ này.

Đây là bài toán do Ơ-clít đưa ra từ thế kỉ III trước Công nguyên. Tỷ số trong bài toán được gọi là tỷ số vàng, và phép chia này gọi là phép chia vàng hoặc phép chia hoàng kim.

Hướng dẫn: Giả sử M là điểm chia đoạn AB và AM lớn hơn MB. Ta gọi tỷ lệ cần tìm là x.

Hướng dẫn giải:

Giả sử M là điểm chia đoạn AB sao cho AM lớn hơn MB, và chiều dài của AB là a.

Đặt độ dài của AM là x; 0 < x < a. Khi đó, MB sẽ là a - x.

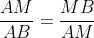
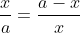
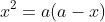
$\displaystyle{\frac{AM}{AB}} = \frac{MB}{AM}$ $\frac{x}{a} = \frac{a - x}{x}$ $x^2 = a \cdot (a - x)$

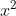
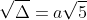
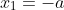
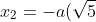
$\Delta = a^2 + 4a^2 = 5a^2$ $\sqrt{\Delta} = a \sqrt{5}$ $\displaystyle x_1 = \frac{-a + a\sqrt{5}}{2} = \frac{a(\sqrt{5} - 1)}{2}$ $x_2 = \frac{-a(\sqrt{5} + 1)}{2}$

Vì x > 0 nên x_2 không đáp ứng yêu cầu của ẩn.

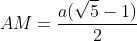
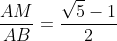
$\displaystyle AM = \frac{a(\sqrt{5} - 1)}{2}$ $\displaystyle \frac{AM}{AB} = \frac{\sqrt{5} - 1}{2}$

Đây là bài viết từ Mytour, hy vọng thông tin trong bài sẽ hữu ích cho bạn. Cảm ơn bạn đã đọc!

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]