Hướng dẫn tính đường chéo của hình vuông và hình chữ nhật

Bạn đang muốn tính đường chéo của hình vuông và hình chữ nhật nhưng lại quên cách tính? Đừng lo, hãy tham khảo ngay bài viết dưới đây để tìm hiểu cách tính đường chéo của hai hình này.

Dưới đây là hướng dẫn cách tính đường chéo cho hình vuông và hình chữ nhật, hãy cùng theo dõi nhé!

Cách tính đường chéo cho hình vuông

Hình vuông trong hình học Euclid được xem như là hình tứ giác đều. Nó có thể coi như là hình chữ nhật với các cạnh bằng nhau hoặc là hình thoi có 2 đường chéo bằng nhau.

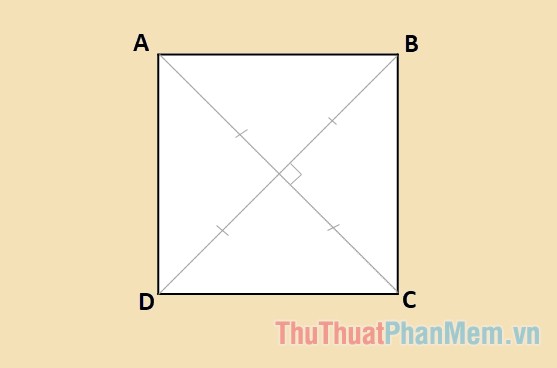
Tính chất của hình vuông

• Trong hình vuông, 2 đường chéo bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
• Có một đường tròn nội tiếp và ngoại tiếp đồng thời tâm của cả hai đường tròn trùng nhau và là giao điểm của hai đường chéo của hình vuông.
• 1 đường chéo sẽ chia hình vuông thành hai phần có diện tích bằng nhau.
• Giao của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.
• Có tất cả tính chất của hình chữ nhật, hình bình hành và hình thoi.

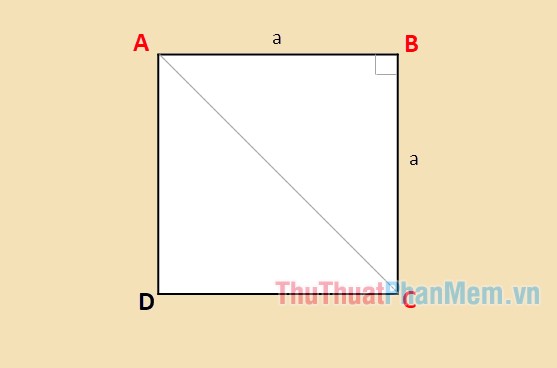
Cách tính đường chéo cho hình vuông

Hai đường chéo hình vuông bằng nhau và chia hình vuông thành hai phần có diện tích bằng nhau. Đường chéo hình vuông chính là cạnh huyền của 2 tam giác vuông cân.

Áp dụng định lý Pythagoras cho tam giác vuông cân ABC:

AC2=AB2+BC2$A{C}^2=A{B}^2+B{C}^2$

HayAC2=a2+a2=2a

Đường chéo hình vuông có độ dài cạnh a là a√2.

Vậy đường chéo hình vuông có độ dài cạnh a là a√2.

Tính đường chéo hình chữ nhật

Hình chữ nhật là một hình tứ giác lồi có bốn góc vuông, là hình bình hành có hai đường chéo bằng nhau.

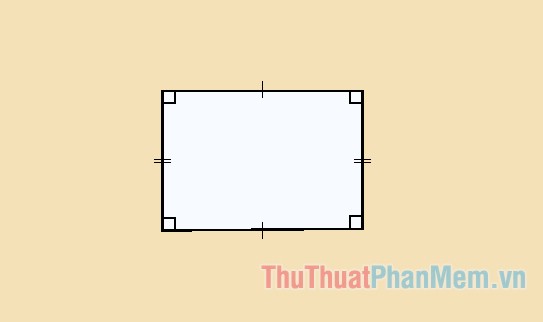
Tính chất của hình chữ nhật

• Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
• Có tất cả các tính chất của hình thang cân và hình bình hành.
• Các đường chéo trong hình chữ nhật cắt nhau tạo thành 4 tam giác cân.

Cách tính đường chéo của hình chữ nhật

Hình chữ nhật có 4 góc vuông, hai đường chéo bằng nhau. Một đường chéo chia hình chữ nhật thành 2 tam giác vuông, và đường chéo chính là cạnh huyền, hai cạnh còn lại là 2 cạnh góc vuông. Để tính đường chéo hình chữ nhật, bạn có thể áp dụng định lý Pythagoras.

Giả sử bạn có hình chữ nhật ABCD, với chiều dài a và chiều rộng b, và đường chéo AC như trong hình.

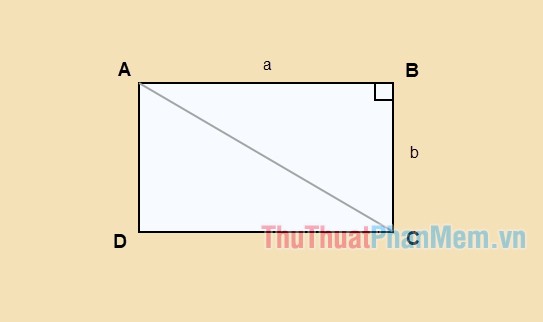
Áp dụng định lý Pythagoras cho tam giác ABC:

AC2=AB2+BC2$A{C}^2=A{B}^2+B{C}^2$

⇔AC2=a2+b2$\iff A{C}^2=a^2+b^2$

Đường chéo hình chữ nhật với chiều dài a và chiều rộng b là √(a2+b2)$\sqrt{\left(a^2+b^2\right)}$

Đường chéo hình chữ nhật với chiều dài a và chiều rộng b là √(a2+b2)$\sqrt{\left(a^2+b^2\right)}$

Chúng ta đã biết cách tính đường chéo hình chữ nhật dễ dàng thông qua định lý Pythagoras. Chúc bạn thành công trong việc tính toán!