1. Hướng dẫn sử dụng máy tính Casio để tính nguyên hàm và tích phân
Nguyên hàm là phép toán ngược của đạo hàm trong phép tính vi phân. Nguyên hàm của một hàm số là hàm số khác mà khi đạo hàm ra sẽ trở về hàm số ban đầu. Ví dụ: Nguyên hàm của hàm số f(x) = 2x là F(x) = x² + C, trong đó C là một hằng số bất kỳ.
Tích phân là phép toán dùng để tính diện tích dưới đồ thị của một hàm số trong khoảng xác định. Tích phân của hàm số từ a đến b là diện tích của vùng nằm giữa đồ thị hàm số, trục hoành và các đường x = a và x = b. Ví dụ: Tích phân của hàm số f(x) = x² từ 0 đến 1 là ∫0,1 dx = (x³/3)|[0,1] = (1/3) - (0/3) = 1/3.
Máy tính Casio có khả năng tính nguyên hàm và tích phân một cách nhanh chóng và chính xác. Để thực hiện chức năng này, hãy làm theo các bước hướng dẫn dưới đây:
Đầu tiên, đặt máy tính ở chế độ MathIO và chọn đơn vị radian.
Tiếp theo, nhấn phím OPTN, sau đó chọn tích phân (ký hiệu ∫) hoặc nguyên hàm (ký hiệu ∫dx).
Sau đó, nhập hàm số cần tính, thiết lập giới hạn dưới và trên (nếu có), biến số (thường là x), và nhấn phím EXE.
Cuối cùng, xem kết quả hiển thị trên màn hình máy tính.
Ví dụ: Để tính nguyên hàm và tích phân của hàm số f(x) = x² + 3x - 5 bằng máy tính Casio, thực hiện như sau:
Nguyên hàm: Nhấn OPTN, chọn ∫dx, nhập x² + 3x - 5, nhấn EXE. Kết quả là F(x) = (x³/3) + (3x²/2) - 5x + C. Tích phân: Nhấn OPTN, chọn ∫, nhập x² + 3x - 5, thiết lập giới hạn dưới là -1, giới hạn trên là 2, biến số x, nhấn EXE. Kết quả là ∫−1,2dx = 0.5
2. Một số bài tập về tính nhanh nguyên hàm và tích phân bằng máy tính Casio
Thiết lập máy: Sai số cực nhỏ 9 chữ số thập phân - Nhấn Shift - mod - 9
Đơn vị radian thường dùng - Nhấn Shift - mod - 4
Thực hiện trên máy tính như sau: d/dx (DA)|= x-X -DB
Tích phân hữu tỷ
Dạng ∫ P(x)/Q(x) với bậc của p(x) >= bậc của Q(x). Thực hiện phép chia đa thức và áp dụng phương pháp CALC 100.
Giả sử Q(x) = (x - x1)(x - x2)(x - x3) (có thể nhiều hơn, nhưng cách làm tương tự):
Biểu thức (x) / Q(x) = A / (x - x1) + B / (x - x2) + C / (x - x3) + R(x) là phần dư của phép chia
Tính A = d/dx (P(x) / ((x - x2)(x - x3))) tại x = x1
Tính B = d/dx (P(x) / ((x - x1)(x - x3))) tại x = x2
Tính C = d/dx (P(x) / ((x - x1)(x - x2))) tại x = x3
Tìm R(x) = d/dx (P(x) / ((x - x1)(x - x2)(x - x3))) - A / (x - x1) - B / (x - x2) - C / (x - x3)) tại x = 100 bằng phương pháp tách 100
Dạng f(x) = (ax + b) / ((x - x1)(x - x2)) cần được tách thành A / (x - x1) + B / (x - x2)
Cách 1. Nhập: (aX + b) /( d/dx (X - x1)(X - x2))|x = X
TÍNH X = x1 -> A
TÍNH X = x2 -> B
Cách 2. Nhập: (aX + b) /(X - x1)(X - x2) x (X - x1)
TÍNH X = x1 + 0,0000001 -> A
TÍNH X = x2 + 0,0000001 -> B
Tách phân thức (ax + b)/(cx + d) thành a/c + K/(cx + d)
Nhập vào máy tính: (aX + b / cX + d - a/c)(cX + d) TÍNH X = 10
Khi đó: ∫ (ax + b) / (cx + d) dx = ∫ (a/c + K / (cx + d)) dx = ax/c + Kc Ln |cx + d|
Bài toán 1: Tìm nguyên hàm F(x) của hàm số f(x)
Cú pháp: f(A) - d/dx(Fi(x))|x = A
Trong đó: f(A) là giá trị của f(x) tại x = A (A là hằng số bất kỳ trong tập xác định, thường lấy giá trị nhỏ như 0,1; 0,2; 0,3...1; 1,1)
F(x) là các kết quả nguyên hàm
Ví dụ:

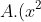
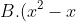
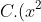
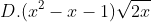
Bước 1: Nhập 5(A² + A) / (sqrt{2A + 1}) - d/dx(x² + x + 1) sqrt{2x+1} | x = A (RCL - A; Shift)
Bước 2: Đặt x = A = 1 hoặc 0,1 (nhấn CALC -> A). Nếu kết quả khác 0, loại ngay đáp án đó -> Loại A
Thay F1(x) bằng đáp án B và gán A như trên, nếu kết quả khác 0 -> Loại B
Thay F1(x) bằng đáp án C và gán A như trên, nếu kết quả bằng 0; để chắc chắn, kiểm tra thêm với các giá trị A như 0; 0,2; 0,5; 1
-> Chọn C (Tránh gán x = A với giá trị quá lớn, máy có thể bị treo)
Bài toán 2: Tìm một nguyên hàm F(x) của hàm số f(x), biết rằng F(x0) = M
Cú pháp: F1(A) - M - ∫(x0->A) f(x) dx
Ví dụ: Tìm nguyên hàm F(x) của hàm số f(x) = (x³ + 3x² + 3x - 1) / (x² + 2x + 1), biết F(1) = 1/3
A. F(x) = x²/2 + x + 2/(x+1) - 6/13
B. F(x) = x²/2 + x + 2/(x+1)
C. F(x) = x²/2 + x + 2/(x+1) + 13/6
D. F(x) = x²/2 + x + 2/(x+1) - 13/6
A²/2 + A + 2/(A+1) - 6/13 - ∫(1-> A) (x³ + 3x² + 3x -1)/(x² + 2x + 1) với A = 0,1; 1 đều cho kết quả khác 0 => loại đáp án A
A²/2 + A + 2/(A+1) - 13/6 - ∫(1-> A) (x³ + 3x² + 3x - 1)/(x² + 2x + 1) với A = 0,1; 1 cho kết quả 0, kiểm tra thêm => chọn D
Bài toán 3: Tính tích phân ∫(a->b) f(x)dx (Các đáp án đều là số vô tỷ, dạng căn, số e, số pi; nên bấm máy để ghi nhận kết quả)
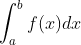
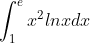
A. (e² + 1)/4
B. (2e³ + 1)/9
C. (3e³ + 2)/8
D. (2e² + 3)/3
(e2 + 1)/4 gần bằng 2,097264025
(2e3 + 1)/9 gần bằng 4,574563716
(3e3 + 2)/8 gần bằng 7,782076346
(2e3 + 3)/3 gần bằng 5,926037399
Bài toán 4: Tính diện tích hình phẳng và thể tích khối tròn xoay
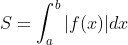
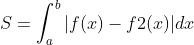
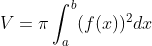
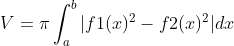
Ví dụ: Diện tích vùng hình phẳng được giới hạn bởi các đồ thị hàm số y = x2 - 2x và y = x là
A. 9/4
B. 9/2
C. 13/4
D. 7/4
Phương trình để tìm hoành độ giao điểm của f1(x) và f2(x) là f1(x) - f2(x) = 0, tương đương với x2 - 3x = 0, nên x = 0 và x = 3
S = ∫(0->1)|x (e^x - e)|dx = e/2 - 1 = 0,35140914
Ví dụ: Khu vực (H) được giới hạn bởi các đường thẳng y = x^2 - 2x; y = 0; x = -1; x = 2. Tính thể tích của hình tròn xoay khi (H) xoay quanh trục Ox
A. 18 π/5 B. 17 π/5
C. 5 π/18 D. 16 π/5
V = π x ∫(-1->2)(x^2 - 2x)^2 dx = 18 π/5
Bài toán 5: Cho hàm số y = f(x) với điều kiện f'(x) = (x + 1) e^x và ∫ f(x)dx = (ax + b). e^x + C, trong đó a và b là các số thực. Tính giá trị của a + b
A. 0
B. 3
C. 2
D. 1
Hàm F(x) = (ax + b)e^x + C là nguyên hàm của f(x) và f'(x) = (x + 1)e^x
Xét F''(x) = f'(x)
∫ f'(x)dx = ∫(x + 1)e^xdx = x.e^x + C = f(x)
∫f(x)dx = ∫x.e^x dx = (x - 1)e^x + C
Do đó, a = 1 và b = -1 nên a + b = 0
Bài toán 6: Cho F(x) là nguyên hàm của hàm số f(x) = 2^x, với điều kiện F(x) = 1/Ln2. Tính giá trị của biểu thức T = F(0) + F(1) + F(2) + ... + F(2017)
A. T = 1009. (2^2017 + 1)/Ln2
B. T = 2^2017.2018
C. T = (2^2017 - 1) / Ln2
D. T = (2^2018 - 1)/Ln2
F(x) = ∫2^xdx = 2^x / Ln2
T = F(0) + F(1) + F(2) + ... + F(2017) = 2^0/Ln2 + 2^1/Ln2 + ... + 2^2017/Ln2 = 1/Ln2 * (2^2018 - 1) = (2^2018 - 1)/Ln2
Sử dụng máy tính: ta có F(x) = 2^x/Ln2
Nhấn SHIFT LOG
Gán kết quả vào A, sau đó trừ đi đáp án đã rút gọn. Chọn D
