Hướng dẫn viết phương trình đường thẳng đi qua hai điểm một cách dễ hiểu và đơn giản

Buzz

Nội dung bài viết

1. Phương pháp viết phương trình đường thẳng qua hai điểm

2. Bài tập về việc xác định phương trình đường thẳng đi qua hai điểm

Xem thêm

Bài viết chi tiết về cách viết phương trình đường thẳng đi qua hai điểm, cung cấp phương pháp giải rõ ràng giúp học sinh ôn tập và thực hành hiệu quả.

1. Phương pháp viết phương trình đường thẳng qua hai điểm

a) Áp dụng định nghĩa

Vấn đề: Cho hai điểm A(a, b) và B(c, d). Tìm phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.

Phương pháp thực hiện:

Bước 1: Tính vectơ chỉ phương của đường thẳng d: AB = (c - a; d - b)

Bước 2: Xác định vectơ pháp tuyến của đường thẳng d: n = (b - d; c - a)

Bước 3: Viết phương trình đường thẳng d: (b - d).(x - a) + (c - a).(y - b) = 0

b) Áp dụng phương trình tổng quát

Bài toán: Xét hai điểm A(a, b) và B(c, d). Viết phương trình tổng quát của đường thẳng đi qua hai điểm này.

Phương pháp thực hiện:

Bước 1: Giả sử phương trình tổng quát của đường thẳng là y = mx + n (*)

Bước 2: Thay tọa độ của các điểm A và B vào phương trình tổng quát để lập hệ phương trình với các ẩn m và n

b = am + n; d = cm + n => (m; n) = (?; ?)

Thay các giá trị m và n vừa tính vào phương trình (*) để tìm ra phương trình đường thẳng mong muốn.

2. Bài tập về việc xác định phương trình đường thẳng đi qua hai điểm

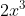
$2x^{3} + 3.(m-1).x^{2} + 6.(m-2).x - 1.$

Bài 2: Với hai điểm A(-2, 3) và B(4, -1), xác định phương trình tổng quát của đường thẳng AB.

Bài 3: Xét phương trình tổng quát 2x - 3y + 6 = 0. Tìm các điểm cắt của đường thẳng với trục hoành và trục tung.

$-x^{2}$

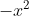
Bài 5: Trong không gian với hệ tọa độ Oxyz, đường thẳng d đi qua hai điểm A (-2; 0; 3) và B (1; 1; 5). Tìm mệnh đề không đúng?

A. Phương trình tham số của d là: Cách đơn giản để viết phương trình đường thẳng qua hai điểm.

B. Phương trình chính tắc của d là: Phương pháp đơn giản để xác định phương trình đường thẳng qua hai điểm.

C. Đường thẳng d đi qua điểm H (-5; -1; 1).

D. Đường thẳng d đi qua điểm K (-11; -3; -3).

Bài 6: Xét tam giác ABC với các đỉnh A (2; -1; 3), B (0; 5; 3), C (2; 1; 4). Chọn mệnh đề không đúng về phương trình đường trung tuyến CN.

A. Phương trình tham số của CN được viết đơn giản: Phương pháp để xác định đường thẳng qua hai điểm.

B. Phương trình chính tắc của CN được xác định dễ dàng: Phương pháp viết phương trình đường thẳng qua hai điểm.

C. Phương trình tham số của CN có thể viết dễ dàng: Phương pháp đơn giản để xác định đường thẳng qua hai điểm.

D. Phương trình chính tắc của CN là: Phương pháp xác định đường thẳng qua hai điểm một cách dễ dàng và rõ ràng.

Bài 7: Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai điểm O (0; 0; 0) và A (-1; 2; -4)?

A. Phương pháp viết phương trình đường thẳng qua hai điểm đơn giản và dễ hiểu.

B. Phương pháp đơn giản để xác định phương trình đường thẳng đi qua hai điểm.

C. Cách viết phương trình đường thẳng qua hai điểm một cách dễ dàng và dễ hiểu.

D. Tất cả các mệnh đề đều sai.

Bài 8: Trong mặt phẳng tọa độ Oxyz, xét tam giác ABC với các đỉnh A (2; 3; 5), B (0; -1; -3) và C (4; -1; -3). Gọi M và N là các trung điểm của AB và AC. Hãy viết phương trình của đường thẳng MN.

A. Phương pháp viết phương trình đường thẳng qua hai điểm một cách đơn giản và dễ hiểu.

B. Cách viết phương trình đường thẳng qua hai điểm theo phương pháp dễ hiểu và đơn giản.

C. Phương pháp dễ dàng để viết phương trình đường thẳng qua hai điểm.

D. Phương pháp viết phương trình đường thẳng qua hai điểm một cách đơn giản và dễ hiểu.

3. Hướng dẫn chi tiết cách viết phương trình đường thẳng qua hai điểm.

Giải thích chi tiết:

Bài 1.

Phương pháp giải:

Cách viết phương trình đường thẳng qua hai điểm một cách đơn giản và dễ hiểu

$(m - 3)^{2}$

Để đường thẳng qua hai điểm cực trị song song với đường thẳng y = -4x + 1, hệ số góc của nó phải là -4

Sử dụng công thức tính nhanh, hệ số góc của đường thẳng đi qua hai điểm cực trị được xác định như sau:

Cách viết phương trình đường thẳng qua hai điểm một cách đơn giản và dễ hiểu

Bài 2.

Để xác định phương trình tổng quát của đường thẳng, có thể dùng hệ số góc của nó:

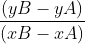
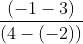
$\frac{(yB - yA)}{(xB - xA)}$ $\frac{(-1 - 3)}{(4 - (-2))}$

Vì điểm A(-2, 3) nằm trên đường thẳng AB, ta có thể dùng điểm này để tính hệ số b của đường thẳng:

y = mx + b => 3 = -0.5 (-2) + b => b = 2

Phương trình tổng quát của đường thẳng AB là: y = -0.5x + 2, hoặc có thể viết dưới dạng chuẩn: 0.5x + y - 2 = 0.

Bài 3

Để xác định điểm giao với trục hoành và trục tung, ta thay x = 0 và y = 0 vào phương trình tổng quát của đường thẳng:

Điểm giao với trục tung: x = 0, 2x - 3y + 6 = 0 => y = 2

Điểm giao với trục hoành: y = 0, 2x - 3y + 6 = 0 => x = 3

Do đó, đường thẳng cắt trục tung tại (0, 2) và cắt trục hoành tại (3, 0).

Bài 4:

Trong bài toán này, tọa độ của các điểm A và B chưa được xác định rõ. Tuy nhiên, chúng ta biết rằng A và B nằm trên đường (P) và đã biết hoành độ. Nhiệm vụ còn lại là tìm tung độ của các điểm A và B.

Tìm tọa độ của điểm A và B:

$-(1)^{2}$ $-(2)^{2}$

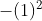
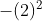
Xét phương trình đường thẳng cần tìm có dạng d: y = ax + b. Vì đường thẳng d đi qua hai điểm A và B nên ta có hệ phương trình:

- 1 = 1.a + b; - 4 = a.2 + b => a = -3; b = 2

Thay giá trị a = -3 và b = 2 vào phương trình d, ta có: y = -3x + 2. Do đó, phương trình đường thẳng qua hai điểm A và B là: y = -3x + 2

Bài 5:

Cách viết phương trình đường thẳng qua hai điểm một cách đơn giản và dễ hiểu

Vì đường thẳng d đi qua hai điểm A và B, vectơ chỉ phương của d được xác định theo cách viết phương trình đường thẳng qua hai điểm đơn giản và dễ hiểu

Do đó, phương trình tham số của d được viết như sau: cách viết phương trình đường thẳng qua hai điểm đơn giản và dễ hiểu

Phương trình chính tắc của d là: cách viết phương trình đường thẳng qua hai điểm đơn giản và dễ hiểu

Khi t = -1, ta có điểm H (-5; -1; 1) nằm trên đường thẳng d.

Khi t = -3, ta có điểm M (-11; -3; -3) thuộc đường thẳng d.

Chọn điểm A.

Bài 6:

Trung điểm A của đoạn AB là N(1; 2; 3)

Cách viết phương trình đường thẳng đi qua hai điểm đơn giản, dễ hiểu => vectơ chỉ phương của CN là u→ = (1; -1; 1)

Do đó, phương trình tham số của đường thẳng CN là: cách viết phương trình đường thẳng đi qua hai điểm đơn giản và dễ hiểu

Phương trình chính tắc của đường thẳng CN là: cách viết phương trình đường thẳng đi qua hai điểm đơn giản và dễ hiểu

Vì vectơ u→ (-1; 1; -1) là vectơ chỉ phương của đường thẳng CN, nên vectơ v→ (-1; 1; -1) cũng là vectơ chỉ phương của đường thẳng CN.

Do đó, đường thẳng CN cũng có phương trình chính tắc là: cách viết phương trình đường thẳng đi qua hai điểm đơn giản và dễ hiểu

Chọn điểm D

Bài 7:

Đường thẳng OA đi qua hai điểm O và A, vì vậy vectơ chỉ phương của nó là: cách viết phương trình đường thẳng đi qua hai điểm đơn giản và dễ hiểu

Do đó, phương trình chính tắc của đường thẳng AB là: cách viết phương trình đường thẳng đi qua hai điểm đơn giản và dễ hiểu

Chọn điểm B

Bài 8:

+ Vì M là trung điểm của đoạn AB, nên tọa độ của M là:

+ Phương trình đường thẳng đi qua hai điểm đơn giản và dễ hiểu => M(1; 1; 1).

+ Tương tự, vì N là trung điểm của đoạn AC, nên tọa độ của N là (3; 1; 1)

+ Đường thẳng MN đi qua điểm M(1; 1; 1) và có vectơ chỉ phương: cách viết phương trình đường thẳng đi qua hai điểm đơn giản và dễ hiểu làm vectơ chỉ phương

=> Phương trình tham số của đường thẳng d là: cách viết phương trình đường thẳng đi qua hai điểm đơn giản và dễ hiểu

Đường thẳng d không có phương trình chính tắc.

Chọn điểm A.

Các câu hỏi thường gặp

Phương trình đường thẳng đi qua hai điểm được viết như thế nào?

Để viết phương trình đường thẳng đi qua hai điểm A(a, b) và B(c, d), bạn cần tính vectơ chỉ phương AB = (c - a; d - b) và vectơ pháp tuyến n = (b - d; c - a). Sau đó, sử dụng công thức để viết phương trình dưới dạng (b - d)(x - a) + (c - a)(y - b) = 0.

Có thể tìm phương trình tổng quát từ tọa độ hai điểm không?

Có, bạn có thể tìm phương trình tổng quát bằng cách giả định y = mx + n, sau đó thay tọa độ của hai điểm vào để lập hệ phương trình tìm ra m và n. Việc này sẽ giúp xác định phương trình tổng quát cần thiết.

Làm thế nào để xác định các điểm cắt của đường thẳng với trục tọa độ?

Để xác định điểm cắt với trục tung và trục hoành, bạn cần thay x = 0 để tìm điểm cắt với trục tung và y = 0 để tìm điểm cắt với trục hoành. Thực hiện các phép tính này trên phương trình tổng quát của đường thẳng.

Có cách nào đơn giản để viết phương trình đường thẳng trong không gian không?

Có, bạn có thể sử dụng phương trình tham số hoặc chính tắc. Đầu tiên, xác định các vectơ chỉ phương và tọa độ của các điểm, từ đó dễ dàng viết phương trình cho đường thẳng trong không gian.

Nội dung từ Mytour nhằm chăm sóc khách hàng và khuyến khích du lịch, chúng tôi không chịu trách nhiệm và không áp dụng cho mục đích khác.

Nếu bài viết sai sót hoặc không phù hợp, vui lòng liên hệ qua email: [email protected]