1. Khái niệm về tiếp tuyến của đồ thị hàm số
Tiếp tuyến là một khái niệm cơ bản trong hình học, đặc biệt khi thảo luận về sự tiếp xúc giữa một đường tròn và một đường thẳng. Tiếp tuyến là đường thẳng duy nhất chạm vào đường tròn tại một điểm duy nhất và vuông góc với bán kính tại điểm đó.
Tiếp tuyến có một đặc điểm quan trọng khác là nó chỉ chạm vào đồ thị tại một điểm duy nhất và không cắt qua đồ thị ở bất kỳ điểm nào khác. Điểm tiếp xúc này là điểm quan trọng trong việc nghiên cứu các thuộc tính và sự tương tác giữa đường tròn và đường thẳng, thể hiện sự giao điểm độc nhất và tương tác đặc biệt giữa hai đối tượng hình học này.
Tiếp tuyến của một đường cong tại bất kỳ điểm nào trên đường cong là một đường thẳng chỉ tiếp xúc với đường cong tại điểm đó. Leibniz đã mô tả tiếp tuyến là đường thẳng nối hai điểm gần nhau vô hạn trên đường cong. Một đường thẳng được coi là tiếp tuyến của đường cong y = f(x) tại điểm x = c nếu nó đi qua điểm (c, f(c)) trên đường cong và có độ dốc f'(c), với f' là đạo hàm của f.
Tiếp tuyến của đồ thị hàm số tại một điểm là một đường thẳng chạm trực tiếp vào đồ thị hàm số tại điểm đó. Để xác định phương trình tiếp tuyến tại điểm M(x1, y1), công thức sử dụng là: y = f'(x1)(x - x1) + y1.
Dựa vào công thức trên, ta thấy rằng đạo hàm bậc nhất của hàm số tại hoành độ của điểm chính là hệ số góc của đường tiếp tuyến.
2. Ý nghĩa hình học của đạo hàm và phương pháp giải
Đạo hàm của hàm số y = f(x) tại điểm x0 là hệ số góc của đường tiếp tuyến với đồ thị (C) của hàm số tại điểm M0(x0; f(x0)).
Phương trình tiếp tuyến của đường cong (C) tại điểm M0 được xác định bằng:
y – y0 = f'(x0) * (x – x0)
Phương pháp giải
Bài toán 1. Xác định phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; f(x0)).
- Tính đạo hàm của hàm số y = f(x)
⇒ f'(x0).
- Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) được cho bởi:
y - y0 = f'(x0) * (x - x0)
Bài toán 2. Xác định phương trình tiếp tuyến của đồ thị hàm số y = f(x) khi biết hoành độ điểm tiếp xúc x = x0.
+ Tính giá trị y0 = f(x0).
+ Tính đạo hàm của hàm số để có f'(x0).
⇒ Phương trình tiếp tuyến là: y - y0 = f'(x0) * (x - x0)
Bài toán 3. Xác định phương trình tiếp tuyến của đồ thị hàm số y = f(x) khi biết tung độ của điểm tiếp xúc là y0.
+ Đặt M(x0; y0) là điểm tiếp xúc.
+ Giải phương trình f(x) = y0 để tìm các giá trị x0.
+ Tính đạo hàm của hàm số để có f'(x0).
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm cụ thể.
3. Xác định phương trình tiếp tuyến của đồ thị hàm số tại một điểm.
Ví dụ 1. Cho hàm số y = x^3 - 2x + 1. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M(0; 1).
A. y = 2x + 3 B. y = -2x + 1 C. y = 4x + 1 D. y = -4x + 1
Hướng dẫn giải quyết bài toán
+ Đạo hàm của hàm số đã cho là: y' = 3x^2 - 2
⇒ y'(0) = -2
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm M(0; 1) được xác định là:
y - 1 = -2(x - 0) hay y = -2x + 1
Chọn đáp án B.
Ví dụ 2. Cho hàm số y = x^2 + 2x - 6. Xác định phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1.
A. y = 2x + 1 B. y = -6x + 1 C. y = 4x - 7 D. y = 3x -
Hướng dẫn cách giải
+ Tính giá trị tại x = 1: y(1) = 1^2 + 2*1 - 6 = -3
+ Đạo hàm của hàm số được cho là: y'(x) = 2x + 2
⇒ y'(1) = 2*1 + 2 = 4
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1 được xác định là:
y + 3 = 4(x - 1) hay y = 4x - 7
Chọn đáp án C.
Ví dụ 3. Cho hàm số y = x^3 + 4x + 2. Xác định phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ y = 2.
A. y = 4x + 2 B. y = -2x + 1 C. y = 3x + 1 D. y = 6x + 1
Hướng dẫn cách giải
+ Giải phương trình: x^3 + 4x + 2 = 2
⇔ x^3 + 4x = 0 ⇔ x = 0
+ Đạo hàm của hàm số đã cho là: y' = 3x^2 + 4
⇒ y'(0) = 4
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ y = 2 là:
y - 2 = 4(x - 0) hay y = 4x + 2
Chọn A.
Ví dụ 4. Cho hàm số y = -x^3 + 2x^2 + 2x + 1 có đồ thị (C). Gọi A là điểm giao nhau của đồ thị (C) với trục tung. Tìm phương trình tiếp tuyến của đồ thị hàm số tại điểm A?
A. y = -2x + 1 B. y = 3x - 2 C. y = 4x + 1 D. y = 2x + 1
Hướng dẫn giải
+ Vì A là điểm giao nhau của đồ thị (C) với trục tung nên tọa độ của A là (0; 1).
+ Đạo hàm của hàm số là y' = -3x^2 + 4x + 2
⇒ y'(0) = 2
⇒ Phương trình tiếp tuyến tại điểm A là:
y - 1 = 2(x - 0) hay y = 2x + 1
Chọn D.
Ví dụ 5. Cho hàm số y = x^2 - 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm giao nhau của đồ thị với trục hoành?
A. y = -x + 1 và y = x - 2 B. y = x + 1 và y = -x + 3
C. y = -2x + 1 và y = x - 2 D. Đáp án khác
Hướng dẫn giải
+ Các giao điểm của đồ thị hàm số với trục hoành là các nghiệm của phương trình:
x^2 - 3x + 2 = 0
Do đó, đồ thị hàm số cắt trục hoành tại hai điểm A(1; 0) và B(2; 0).
+ Đạo hàm của hàm số là: y' = 2x - 3
+ Tại điểm A(1; 0), ta tính được: y'(1) = -1
⇒ Phương trình tiếp tuyến tại điểm A là:
y - 0 = -1(x - 1) hay y = -x + 1
+ Tại điểm B(2; 0), đạo hàm là y'(2) = 1
⇒ Phương trình tiếp tuyến tại điểm B là:
y - 0 = 1(x - 2) hay y = x - 2
Vậy, các tiếp tuyến thỏa mãn là: y = -x + 1 và y = x - 2
Chọn A.
Ví dụ 6. Xét hai đường thẳng d1: 2x + y - 3 = 0 và d2: x + y - 2 = 0. Điểm A là giao điểm của hai đường thẳng này. Cho hàm số y = x² + 4x + 1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm A.
A. y = 3x - 5 B. y = 6x + 1 C. y = 6x - 5 D. y = 2x + 1
Hướng dẫn giải
+ Điểm A là nghiệm của hệ phương trình từ hai đường thẳng d1 và d2.
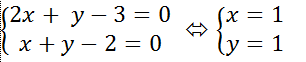
Vậy hai đường thẳng đã cho giao nhau tại điểm A(1; 1).
+ Đạo hàm của hàm số là: y’ = 2x + 4
⇒ y’(1) = 6.
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm A(1; 1) là:
y - 1 = 6(x - 1) hay y = 6x - 5
Chọn đáp án C.
Ví dụ 7: Xét hàm số y =x^4 + 2x^2 + 1 với đồ thị (C). Gọi d là tiếp tuyến của đồ thị tại điểm có hoành độ nguyên dương nhỏ nhất. Đường thẳng d sẽ song song với đường thẳng nào dưới đây?
A. y = -6x B. y = 8x C. y = -10x D. y = 12x
Hướng dẫn giải bài tập
+ Đạo hàm của hàm số là: y’ = 4x^3 + 4x
+ Điểm có hoành độ nguyên dương nhỏ nhất là 1. Ta xác định phương trình tiếp tuyến của đồ thị (C) tại điểm này.
+ Tính toán cho ta: y’(1) = 8 và y(1) = 4
⇒ Phương trình tiếp tuyến của đồ thị hàm số (C) tại điểm hoành độ 1 là:
y - 4 = 8(x - 1) hay y = 8x - 4
⇒ Đường thẳng d sẽ song song với đường thẳng y = 8x
Chọn đáp án B.
Ví dụ 8: Phương trình của tiếp tuyến tại điểm có hoành độ x = 2 của đồ thị hàm số y = (x - 1)^2(x - 2) là
A. y = -2x - 1 B. y = x + 1 C. y = 3x + 1 D. y = x - 2
Hướng dẫn giải bài toán
+ Gọi M(x0; y0) là tọa độ của điểm tiếp xúc.
Với x0 = 2 thì y0 = 0
+ Ta có: y = (x - 1)^2(x - 2) = (x^2 - 2x + 1)(x - 2)
Vậy y = x^3 - 4x^2 + 5x - 2
⇒ Đạo hàm của hàm số là: y’ = 3x^2 - 8x + 5
⇒ y’(2) = 1
Vậy phương trình của tiếp tuyến là:
y - 0 = 1(x - 2) hay y = x - 2
Chọn đáp án D.
