1. Hàm số chẵn là gì?
Một cách trực quan, hàm số chẵn hoặc lẻ có đồ thị mà trục tung là trục đối xứng (đối với hàm số chẵn) hoặc gốc tọa độ là tâm đối xứng (đối với hàm số lẻ). Điều này có nghĩa là tập xác định của hàm số cần phải đối xứng qua điểm x=0. Tức là, với mọi giá trị thuộc tập xác định của hàm số, giá trị đối của nó cũng phải nằm trong tập xác định.
Ví dụ:
Tập số (−1;1) có tính đối xứng qua điểm x=0.
Tập số [−1;1) không có tính đối xứng qua điểm x=0.
Hàm số y = f(x) với tập xác định D được gọi là hàm số chẵn nếu nó thỏa mãn hai điều kiện sau đây:
Điều kiện 1: ∀ x ∈ D ⇒ −x ∈ D
Điều kiện 2: ∀ x ∈ D : f(−x) = f(x)
Ví dụ: Hàm số y = x² là một hàm số chẵn.
Đồ thị của hàm số chẵn có trục tung Oy là trục đối xứng. Vì vậy, nếu bạn chọn một điểm bất kỳ với tọa độ (x; f(x)) trên đồ thị, thì điểm đối xứng qua trục tung, (-x; f(−x)), cũng nằm trên đồ thị của hàm số y = f(x), và rõ ràng là f(−x) = f(x).
Các hàm số chẵn thường gặp
y = ax² + bx + c khi và chỉ khi b = 0
Hàm số bậc 4 có dạng trùng phương
y = cos(x)
2. Hàm số lẻ là gì?
Hàm số y = f(x) với tập xác định D được gọi là hàm số lẻ nếu nó thỏa mãn các điều kiện sau đây:
Điều kiện 1: ∀ x ∈ D ⇒ −x ∈ D
Chú ý: Điều kiện này còn được gọi là tập xác định đối xứng qua gốc tọa độ. Ví dụ, D = (-2;2) là tập đối xứng qua gốc tọa độ, trong khi D' = [-2;3] không phải là tập đối xứng qua 0. Tập R = (−∞;+∞) là tập đối xứng.
Điều kiện 2: ∀ x ∈ D : f(−x) = −f(x)
Ví dụ: Hàm số y = x là một hàm số lẻ.
Đồ thị của hàm số lẻ có gốc tọa độ O là tâm đối xứng. Do đó, nếu chọn một điểm bất kỳ (x; f(x)) trên đồ thị, thì điểm đối xứng qua gốc tọa độ, (-x; f(−x)), cũng nằm trên đồ thị của hàm số y = f(x). Vì hai điểm này đối xứng qua gốc tọa độ, nên f(−x) = −f(x).
Các hàm số lẻ thường gặp
y = ax + b khi và chỉ khi b = 0
y = ax³ + bx² + cx + d khi và chỉ khi b = d = 0
y = sin(x); y = tan(x); y = cot(x)
Hàm số không chẵn và không lẻ là gì?
Không phải tất cả các hàm số đều có thể được phân loại là hàm số chẵn hoặc lẻ. Một số hàm số không thuộc loại chẵn cũng không thuộc loại lẻ, ví dụ như: y = x² + x, y = tan(x-1), …
Ví dụ: Hàm số y = 2x + 1 không phải là hàm số chẵn cũng như không phải là hàm số lẻ vì:
Khi x = 1, ta có f(1) = 2.1 + 1 = 3
Khi x = -1, ta có f(-1) = 2.(-1) + 1 = -1
→ Hai giá trị f(1) và f(-1) không bằng nhau và cũng không phải là giá trị đối nhau.
Ngoài ra, cũng tồn tại một loại hàm số đặc biệt vừa chẵn vừa lẻ, ví dụ như hàm y = 0.
Chứng minh:
Dễ dàng nhận thấy hàm số y = 0 là một hàm số xác định trên toàn bộ R, đồng thời vừa là hàm số chẵn, vừa là hàm số lẻ. Giả sử hàm số y = f(x) có các tính chất như vậy. Khi đó, với mọi x thuộc R, ta có:
F(–x) = f(x) (vì f là hàm số chẵn);
F(–x) = –f(x) (vì f là hàm số lẻ).
Do đó, với mọi x thuộc R, ta có f(x) = –f(x), tức là f(x) = 0. Vậy, hàm số y = 0 là hàm số duy nhất trên R vừa chẵn vừa lẻ.
3. Xác định tính chất chẵn lẻ của hàm số
3.1. Một số đặc điểm của hàm số chẵn và lẻ để nhận diện
- Nếu F(x) là hàm số chẵn và có đạo hàm trên tập xác định, thì đạo hàm của nó sẽ là hàm số lẻ.
- Nếu F(x) là hàm số lẻ và có đạo hàm trên tập xác định, thì đạo hàm của nó sẽ là hàm số chẵn.
- Các hàm số đa thức có bậc lẻ không thể là hàm số chẵn.
- Các hàm số đa thức có bậc chẵn không thể là hàm số lẻ.
3.2. Cách nhận diện hàm số chẵn và hàm số lẻ dựa trên các điều kiện cơ bản
Để xác định xem một hàm số có phải là hàm chẵn hoặc lẻ hay không, ta thực hiện các bước sau đây:
Bước 1: Xác định tập xác định: D
Nếu với mọi x ∈ D thì -x cũng thuộc D, chuyển sang bước tiếp theo.
Nếu tồn tại x0 ∈ D sao cho -x0 không thuộc D, thì hàm số không phải là hàm chẵn cũng không phải là hàm lẻ.
Bước 2: Thay x bằng -x và tính giá trị f(-x)
Bước 3: So sánh giá trị (so sánh f(x) với f(-x)):
- Nếu f(-x) = f(x), thì hàm số f là hàm chẵn
- Nếu f(-x) = -f(x), thì hàm số f là hàm lẻ
- Trong các trường hợp khác, hàm số f không thuộc loại hàm chẵn hay lẻ
Ví dụ: (Bài 4 trang 39 Sách giáo khoa Đại số 10) Xem xét tính chẵn lẻ của các hàm số dưới đây:
a) y = |x|; b) y = (x + 2)2; c) y = x3 + x; d) y = x2 + x + 1.
Hướng dẫn giải:
a) Xét y = f(x) = |x|.
+ Tập xác định: D = R, vì vậy với mọi x ∈ D thì -x cũng thuộc D.
+ f(-x) = |-x| = |x| = f(x).
→ Do đó, hàm số y = |x| là một hàm số chẵn.
b) Xét y = f(x) = (x + 2)2.
+ Tập xác định: D = R, vì vậy với mọi x ∈ D thì –x cũng nằm trong D.
+ f(-x) = (-x + 2)^2 = (x - 2)^2 ≠ (x + 2)^2 = f(x)
+ f(-x) = (-x + 2)^2 = (x - 2)^2 ≠ - (x + 2)^2 = -f(x).
→ Do đó, hàm số y = (x + 2)^2 không phải là hàm số chẵn cũng không phải là hàm số lẻ.
c) Xét y = f(x) = x^3 + x.
+ Tập xác định: D = R, vì vậy với mọi x ∈ D thì –x cũng thuộc D.
+ f(-x) = (-x)^3 + (-x) = -x^3 - x = - (x^3 + x) = -f(x)
→ Do đó, y = x^3 + x là hàm số lẻ.
d) Xét y = f(x) = x^2 + x + 1.
+ Tập xác định: D = R, vì vậy với mọi x ∈ D thì –x cũng nằm trong D.
+ f(-x) = (-x)^2 + (-x) + 1 = x^2 - x + 1 ≠ x^2 + x + 1 = f(x)
+ f(-x) = (-x)^2 + (-x) + 1 = x^2 – x + 1 ≠ -(x^2 + x + 1) = -f(x)
→ Do đó, hàm số y = x^2 + x + 1 không phải là hàm số chẵn cũng không phải là hàm số lẻ.
3.3. Phương pháp xác định hàm số chẵn lẻ qua đồ thị hàm số
Dựa vào đồ thị hàm số: Như đã biết, đồ thị của hàm số chẵn (hoặc lẻ) có tính đối xứng qua trục tung (hoặc gốc tọa độ), vì vậy chúng ta có thể nhận diện qua quan sát đồ thị.
3.4. Phương pháp xác định hàm số chẵn lẻ bằng máy tính
Sử dụng máy tính Casio để kiểm tra bằng cách so sánh giá trị f(x) và f(-x) để thấy sự tương đương hoặc đối ngược. Để thực hiện, sử dụng chức năng Table trong chế độ hai hàm số.
Ví dụ: Xem xét tính chẵn lẻ của hàm số y = x³ + 2x² - 3
Giải: Trên máy tính cầm tay Vinacal 570 ES Plus II, thực hiện các bước sau (các máy tính bỏ túi khác cũng làm tương tự):
MODE 7 Nhập hàm số được cho trong đề bài.
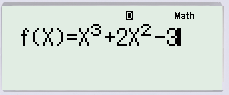
Tiếp theo, nhập hàm số g(x)=f(−x) (Tức là thay x bằng −x trong hàm số).
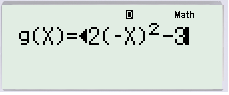
Các mục START, END, STEP có thể để mặc định để tiết kiệm thời gian (có thể thay đổi nếu muốn). Kết quả thu được như sau:
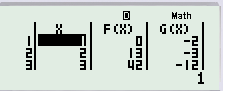
Khi so sánh hai cột giá trị F(X) và G(X) tại x=1, thấy rằng các giá trị không bằng nhau và cũng không đối nhau. Vì vậy, hàm số đã cho không phải là hàm chẵn cũng không phải là hàm lẻ. Phương pháp này chỉ mang tính chất ước lượng và không thể thay thế cho chứng minh chính thức, nhưng có thể áp dụng trong các bài toán trắc nghiệm.
