1. Số phức là gì?
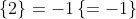
Trong công thức này, phần a được gọi là phần thực và phần b là phần ảo của số phức. Số phức có thể được biểu diễn trên mặt phẳng phức với trục x là trục thực và trục y là trục ảo, vì vậy số phức a + b tương ứng với điểm (a, b) trên mặt phẳng đó.
Một số phức có phần thực bằng 0 được gọi là số thuần ảo, trong khi số phức có phần ảo bằng 0 trở thành số thực. Số phức được mở rộng để giải quyết các bài toán không thể giải trong tập số thực.
- Công thức lượng giác
- Diện tích tam giác
Số phức có dạng a + bi
Trong đó: a, b là các số thực
i là đơn vị ảo trong số phức
Với i^2 = -1
i^2 = -1
Khi ta lấy phần thực của số phức, kết quả là a. Khi ta lấy phần ảo của số phức, kết quả là b.
Ví dụ: Số phức là
Với số phức 2 + 3i, phần thực là 2 và phần ảo là 3
Số 4.4 = 4.4 + 0i cho thấy hệ số của phần ảo b bằng 0 trong trường hợp này
Như vậy, số phức có thể coi là một dạng tổng quát hơn của số thực. Số thực là một trường hợp đặc biệt của số phức khi b = 0.
2. Lý thuyết về số phức
1. Số phức liên hợp
Định nghĩa: Số phức liên hợp có dạng Z = a + bi, trong đó số phức
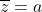
Số phức liên hợp có những đặc điểm như sau:
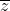
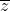
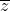
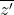
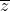
2. Số phức nghịch đảo
Số phức nghịch đảo, ký hiệu là Z⁻¹, là số phức sao cho khi nhân với số phức Z sẽ cho kết quả bằng 1.
- Nghịch đảo của số phức Z = a + bi được tính bằng Z⁻¹ = 1 / (a + bi)
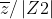
3. Số phức thuần ảo
Định nghĩa: Số phức thuần ảo là số có phần thực a = 0, tức là Z = bi, trong đó Z thuộc tập số ảo. Khi đó, Z được gọi là số thuần ảo.
4. Độ lớn của số phức
Modun của số phức Z = a + bi chính là độ dài của vector (a, b) đại diện cho số phức đó.
Theo một cách định nghĩa khác, modun của số phức Z = a + bi, với a và b thuộc R, là căn bậc hai của tổng bình phương a² + b².
Ví dụ: Modun của 3 + 4i là 5
Modun của 3 + 4i là 5
Trị tuyệt đối của số thực chính là modun của nó. Vì vậy, đôi khi modun của số phức cũng được gọi là trị tuyệt đối của số phức.
Về mặt hình học, mỗi số phức Z = a + bi với a và b thuộc R được biểu diễn bằng điểm M(z) = (a, b) trên mặt phẳng tọa độ O(xy). Modun của Z là độ dài của đoạn thẳng OM(z). Modun của z là một số thực không âm và chỉ bằng 0 khi z = 0.
3. Một số bài tập cơ bản về số phức
Dạng 1: Các quỹ tích đơn giản cơ bản:
Đường thẳng: Quỹ tích của các điểm M biểu diễn số phức z = x + yi là một đường thẳng nếu tọa độ M(x; y) thỏa mãn phương trình đường thẳng: Ax + By + C = 0
Đường tròn: Quỹ tích của các điểm M biểu diễn số phức z = x + yi là một đường tròn nếu tọa độ M(x; y) thỏa mãn phương trình đường tròn: (x - a)² + (y - b)² = R², trong đó I(a; b) là tâm và R là bán kính của đường tròn.
Đường elip là tập hợp tất cả các điểm M biểu thị số phức z = x + yi nằm trên đường elip nếu M(x; y) thỏa mãn phương trình (E): x²/a² + y²/b² = 1, trong đó a và b lần lượt là các bán trục lớn và bán trục nhỏ của elip.
Dạng 2: Các bài toán tìm phần thực hoặc phần ảo của số phức.
Chuyển số phức đã cho về dạng z = a + bi, trong đó a và b là các số thực. Phần thực của z là a và phần ảo của z là b. Lưu ý rằng khi đề bài yêu cầu tìm phần ảo của số phức, có thể xuất hiện các phương án gây nhiễu.
Dạng 3: Bài tập với số phức có mũ cao.
Để tính số phức với mũ cao, chúng ta sử dụng dạng lượng giác hoặc dạng mũ của số phức. Áp dụng công thức lượng giác tương ứng để giải quyết bài toán.
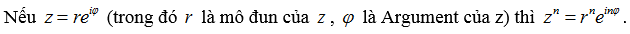
Dạng 4: Các bài toán liên quan đến phương trình bậc 2 với hệ số thực trong tập số phức.
Đối với phương trình bậc 2 với hệ số thực trong tập số phức, chúng ta phân loại thành hai nhóm: nhóm bài tập tìm nghiệm và nhóm bài tập áp dụng định lý Viet. Đối với phương trình không có tham số, thường dùng máy tính bỏ túi để tính toán, còn khi có tham số, ta tính delta rồi áp dụng công thức nghiệm hoặc định lý Viet.
Câu 1: Xác định phần thực và phần ảo của các số phức sau đây:
a. z = -3 + 5i
b. z = 12
c. z = (4 - i) + (2 + 3i)
d. z = (2 + i) - (1 + 4i)
e. z = (11 - 6i) - (2 - 4i)
f. z = (1 + i)² - (1 - i)²
g. z = (11 - 6i) - (2 - i)
Câu 2: Tìm các giá trị thực x, y thỏa mãn:
a. (2x + 1) + 5i = -4 + (3y - 2)i
b. (x - 2) - 4i = 3 - (y + i)
Câu 3: Tìm số phức liên hợp của mỗi số phức và tính giá trị module của chúng.
a. z = 2 - 5i
b. z = 7i
c. x = 6 + i
d. z = 4 - i
Câu 4: Biểu diễn các số phức sau dưới dạng đại số
a. z = 1 / (i + 1) + (4 - 3i)
b. z = 1 / (2 - 3i)
c. z = (3 + 4i) / (4 - i)
d. a = 1 / (2 - 3i)
Câu 5: Trên mặt phẳng phức, xác định tập hợp các điểm biểu diễn số phức z thoả mãn điều kiện sau:
a. Phần thực của số phức z gấp đôi phần ảo của nó
b. Phần thực của số phức z nằm trong khoảng từ -2 đến 1
c. Phần thực của số phức z nằm trong khoảng từ -2 đến 1 và phần ảo của nó nằm trong khoảng từ 1 đến 3
Câu 6: Cho số phức z = a + bi. Điều kiện nào cần để a và b thỏa mãn?
a. Điểm biểu diễn của số phức phải nằm giữa hai đường thẳng x = -2 và x = 2
b. Điểm biểu diễn của chúng nằm giữa hai đường thẳng y = -3i và y = 3i
c. Điểm biểu diễn nằm trong vòng tròn có tâm O và bán kính 2
Câu 7: Tìm tập hợp các điểm biểu diễn của các số phức z trên mặt phẳng tọa độ sao cho chúng thỏa mãn các điều kiện sau:
a. Phần thực của số phức z bằng 2
b. Phần ảo của số phức z nằm trong khoảng (-1; 3)
Phần thực và phần ảo của số phức z nằm trong khoảng [-2; 2]
Câu 8: Tính giá trị biểu thức T = x + y với x và y là số thực, sao cho (x + i) (1 + yi) - (2 + 3yi) là số thuần ảo và (2x - 3) (i + 1) - 3 + y là số thực
Câu 9: Tìm số phức liên hợp của z = i (3i + 1)
Câu 10: Cho số phức z = a + bi với a, b thuộc R, thỏa mãn (1 + i)z + 2z = 3 + 2i. Tính P = a + b
Câu 11: Cho số phức z = a + bi với a, b thuộc R. Biết tập hợp các điểm A biểu diễn số phức z là hình tròn (C) có tâm I(4; 3) và bán kính R = 3. Xác định giá trị lớn nhất M và giá trị nhỏ nhất m của F = 4a + 3b - 1. Tính M + m
Bài viết trên Mytour đã cung cấp cho bạn đọc thông tin chi tiết về số phức, bao gồm định nghĩa, lý thuyết và các dạng bài tập cơ bản. Bài viết cũng trình bày rõ ràng đáp án và các nội dung liên quan. Cảm ơn bạn đã quan tâm theo dõi.
