 Khái niệm thuật toán là gì? Chức năng và đặc điểm của thuật toán
Khái niệm thuật toán là gì? Chức năng và đặc điểm của thuật toánHiện nay, các công ty công nghệ và điện tử xem thuật toán như một tiêu chí quan trọng để đánh giá kiến thức của ứng viên. Đây cũng là chủ đề mà lập trình viên cần nắm vững để làm việc hiệu quả trong nghề. Bài viết này sẽ cung cấp cho bạn những kiến thức cơ bản về thuật toán: Khái niệm thuật toán, vai trò và đặc điểm của thuật toán, cũng như nhận diện 12 loại thuật toán dành cho lập trình viên.
I. Khái niệm thuật toán là gì?
Thuật toán được hiểu là một tập hợp các quy tắc và hướng dẫn mà ta cần tuân theo để thực hiện các phép tính hoặc giải quyết các vấn đề khác. Nó cũng có thể được coi là một quy trình để giải quyết một bài toán thông qua một số bước nhất định, thường bao gồm các phép toán đệ quy.
 Khái niệm về thuật toán là gì
Khái niệm về thuật toán là gìVì vậy, thuật toán là một chuỗi các bước hữu hạn nhằm giải quyết một vấn đề cụ thể. Độ phức tạp của các thuật toán có thể khác nhau, tùy thuộc vào mục tiêu bạn muốn đạt được. Chẳng hạn: Khi muốn nấu một món ăn mới, người ta thường đọc và thực hiện từng bước trong hướng dẫn. Nhờ vậy, món ăn mới sẽ hoàn tất.
Mỗi khi bạn sử dụng điện thoại, máy tính, laptop hay máy tính bỏ túi, bạn đều đang áp dụng thuật toán. Hơn nữa, các thuật toán cũng giúp thực hiện các nhiệm vụ trong lập trình để đạt được kết quả đầu ra như mong đợi. Thuật toán được phát triển một cách độc lập với ngôn ngữ lập trình, nghĩa là chúng chỉ là những hướng dẫn đơn giản có thể được thực hiện bằng bất kỳ ngôn ngữ nào và kết quả sẽ luôn giống nhau.
II. Ý nghĩa của thuật toán
 Ý nghĩa của thuật toán là gì
Ý nghĩa của thuật toán là gìThuật toán giữ một vai trò thiết yếu trong các chương trình máy tính và phần mềm. Ý nghĩa của thuật toán là gì:
Quản lý tài nguyên hiệu quả: Phần mềm máy tính sử dụng nhiều tài nguyên, bao gồm cơ sở dữ liệu, bộ nhớ, thư viện và bộ đệm. Thuật toán giúp điều phối các hoạt động trong phần mềm và bảo đảm rằng chương trình máy tính vận hành một cách mượt mà.
Quản lý năng lượng tiêu thụ: Mọi chương trình máy tính đều cần điện để hoạt động. Một số ứng dụng tiêu tốn nhiều năng lượng hơn so với những ứng dụng khác. Thuật toán có nhiệm vụ điều chỉnh lượng điện năng mà các chương trình cần sử dụng trong một khoảng thời gian nhất định.
Tối ưu hóa hiệu suất của các chương trình máy tính: Thuật toán xem xét các nguồn lực hiện có, nhu cầu năng lượng và thời gian cần thiết để giải quyết vấn đề.
 Ý nghĩa của thuật toán là gì: Nâng cao trải nghiệm của người dùng
Ý nghĩa của thuật toán là gì: Nâng cao trải nghiệm của người dùngTăng cường tốc độ thực hiện: Các thuật toán được thiết kế để nâng cao tốc độ hoạt động một cách đáng kể. Mục tiêu là đảm bảo rằng các nhiệm vụ hiện tại không mất quá nhiều thời gian để hoàn thành và không gây ra sự chậm trễ không cần thiết. Chính nhờ đặc điểm này, các thuật toán và máy tính nói chung có thể xử lý nhiều nhiệm vụ đồng thời mà không gặp khó khăn lớn.
Cải thiện trải nghiệm trên mạng xã hội: Thuật toán quyết định bài viết nào sẽ được hiển thị và quảng cáo nào là phù hợp trên nguồn cấp dữ liệu của người dùng. Chẳng hạn, thuật toán của Facebook phân tích các loại bài viết và trang mà mỗi người dùng tương tác. Từ đó, nó lựa chọn và hiển thị các bài viết cũng như quảng cáo có chủ đề tương tự.
III. Phân loại thuật toán
1. Phân loại theo đặc điểm
Theo cách phân loại này, thuật toán được chia thành ba loại cơ bản: thuật toán tìm kiếm, thuật toán sắp xếp và thuật toán đồ thị. Cụ thể:
- Thuật toán tìm kiếm: là loại thuật toán được sử dụng để truy xuất thông tin và dữ liệu trong một tập hợp bao gồm nhiều phần tử khác nhau.
- Thuật toán sắp xếp: giúp tổ chức các phần tử trong một tập hợp theo thứ tự hợp lý và khoa học.
- Thuật toán đồ thị: là loại thuật toán dùng để giải quyết các vấn đề liên quan đến đồ thị.
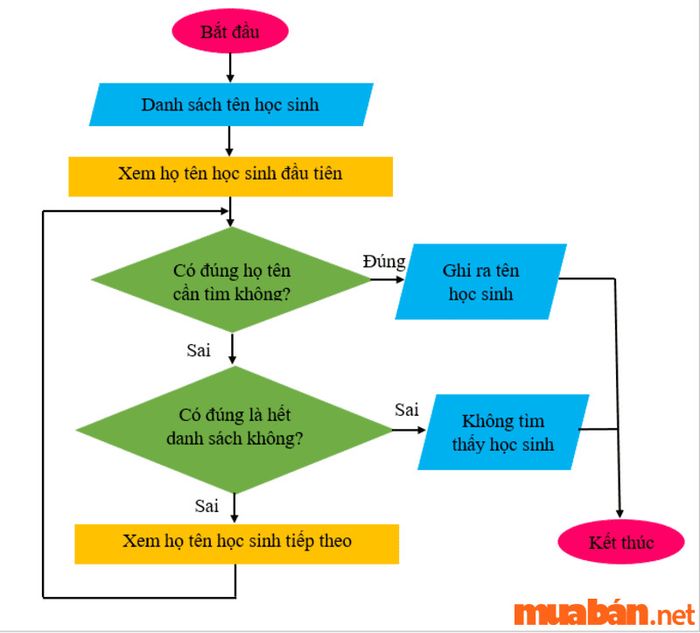 Một ví dụ minh họa cho cách THUẬT TOÁN TÌM KIẾM hoạt động
Một ví dụ minh họa cho cách THUẬT TOÁN TÌM KIẾM hoạt động2. Phân loại theo phương pháp thực hiện
Theo phân loại thuật toán dựa trên phương pháp thực hiện, có hai loại chính: thuật toán chia để trị và thuật toán tham lam. Vậy hai thuật toán này là gì và có ý nghĩa như thế nào?
- Thuật toán chia để trị: phân chia bài toán lớn thành những phần nhỏ hơn, xử lý từng vấn đề nhỏ để giải quyết dần dần.
- Thuật toán tham lam: giúp thay đổi trạng thái của bài toán thông qua những hành động cụ thể, cho phép người giải quyết tiếp cận vấn đề từ từ để tìm ra giải pháp hiệu quả nhất.
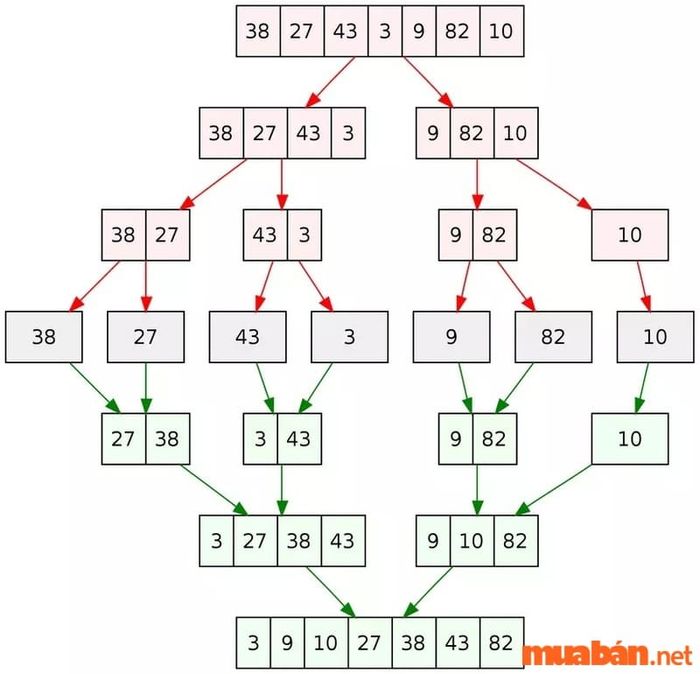 thuật toán là gì: Thuật toán chia để trị
thuật toán là gì: Thuật toán chia để trịIV. Các đặc điểm của thuật toán
1. Độ chính xác
Độ chính xác là một trong những đặc tính nổi bật khi nói đến thuật toán. Sự chính xác cao của thuật toán đảm bảo rằng các kết quả đạt được là hiệu quả và khả thi hơn trong việc giải quyết các bài toán và công thức.
2. Độ rõ ràng và minh bạch
Đặc tính thứ hai của thuật toán là gì? Đó chính là độ rõ ràng và minh bạch. Tính rõ ràng được thể hiện qua các nguyên tắc lệnh. Mỗi câu lệnh trong thuật toán cần được diễn đạt một cách rõ ràng, dễ hiểu và được sắp xếp theo một trình tự hợp lý.
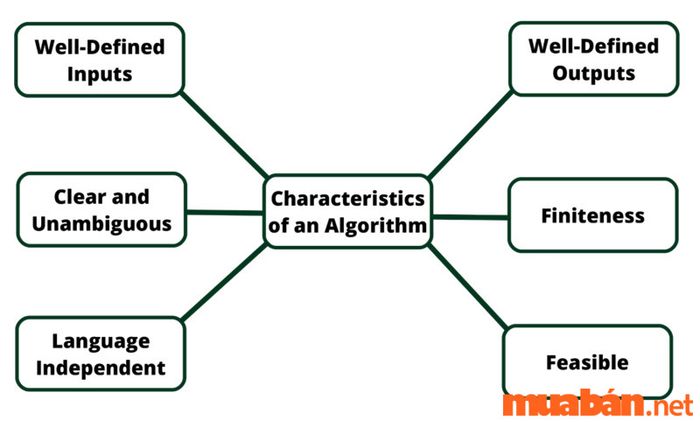 Đặc tính của thuật toán là gì?
Đặc tính của thuật toán là gì?3. Tính khách quan
Tính khách quan là một đặc điểm nổi bật của thuật toán. Dù được thực hiện theo cách nào, kết quả nhận được vẫn phải giống nhau. Nếu kết quả từ hai phương pháp khác nhau không tương thích, người thực hiện cần xem xét lại, vì điều đó chứng tỏ thuật toán có thể sai hoặc không hợp lý.
4. Tính ứng dụng rộng rãi
Tính ứng dụng rộng rãi cũng là một đặc điểm quan trọng của thuật toán. Thuật toán không chỉ được dùng để giải quyết một bài toán đơn lẻ mà còn có khả năng áp dụng vào nhiều vấn đề khác nhau trong cuộc sống.
5. Tính kết thúc
Mỗi thuật toán đều phải có tính kết thúc hay kết quả đầu ra. Bởi vì thuật toán là một tập hợp hữu hạn, nó luôn có một điểm kết thúc. Điểm kết thúc của thuật toán chính là kết quả phù hợp đã được tìm ra.
V. Khám phá 12 loại thuật toán cơ bản dành cho lập trình viên (IT)
 thuật toán là gì
thuật toán là gìViệc tìm kiếm một thuật toán tốt nhất và chính xác là điều cần thiết để giúp chương trình máy tính đạt được thành công. Sau khi hiểu rõ thuật toán là gì, Mytour xin giới thiệu 12 loại thuật toán hàng đầu thường được sử dụng trong lập trình và phát triển web:
1. Thuật toán Hashing
Hashing là một thuật toán giúp phát hiện và xác định dữ liệu thích hợp thông qua các key và ID. Vai trò chính của hashing bao gồm phát hiện lỗi, quản lý bộ nhớ cache, tra cứu và bảo mật. Hàm hashing hoạt động như một định danh duy nhất cho các tập dữ liệu và thực hiện tính toán để tạo ra các giá trị dữ liệu không trùng lặp. Thông thường, hàm hashing được áp dụng trong các bộ định tuyến để lưu trữ địa chỉ IP.
Nếu bạn làm việc trong lĩnh vực bảo mật, việc nắm rõ các thông tin chi tiết về bảo vệ là rất quan trọng. Thuật toán Hashing là một lựa chọn xuất sắc để đảm bảo rằng dữ liệu hoặc mật khẩu của bạn không bị đánh cắp bởi những kẻ xấu. Về cơ bản, hàm hashing chuyển đổi một dữ liệu đầu vào có độ dài bất kỳ thành một chuỗi đầu ra có độ dài cố định.
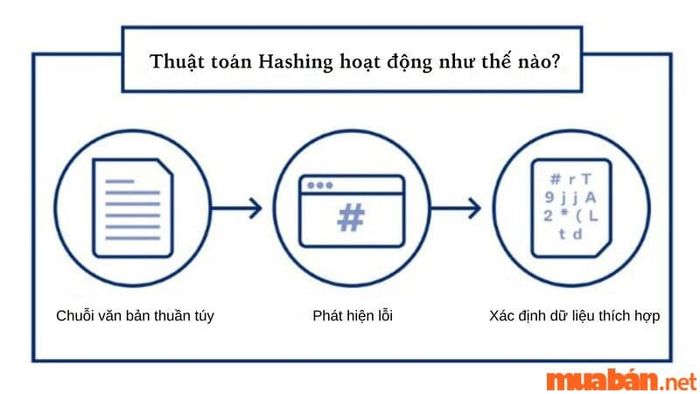 thuật toán là gì: Thuật toán Hashing
thuật toán là gì: Thuật toán HashingVí dụ: Giả sử chúng ta muốn sử dụng hàm băm cho một câu hỏi bảo mật. Chúng ta hỏi, “Nhà đầu tiên của bạn ở đâu?” Câu trả lời nhận được là “Tầng thượng của tòa Vinhomes Ocean Park.” Đây chính là cách mà thuật toán Hashing hoạt động:
- MD5: 72b003ba1a806c3f94026568ad5c5933
- SHA-256: f6bf870a2a5bb6d26ddbeda8e903f3867f729785a36f89bfae896776777d50af
Với câu hỏi tương tự, chúng tôi nhận được câu trả lời từ một người khác là “Chicago”. Kết quả khi áp dụng hàm băm sẽ như sau:
- MD5: 9cfa1e69f507d007a516eb3e9f5074e2
- SHA-256: 0f5d983d203189bbffc5f686d01f6680bc6a83718a515fe42639347efc92478e
Cần lưu ý rằng các tin nhắn ban đầu không có cùng độ dài ký tự. Nhưng các thuật toán vẫn tạo ra giá trị băm với độ dài nhất quán mỗi lần. Và cũng cần chú ý rằng các giá trị băm này hoàn toàn không thể phục hồi.
2. Thuật toán tìm kiếm
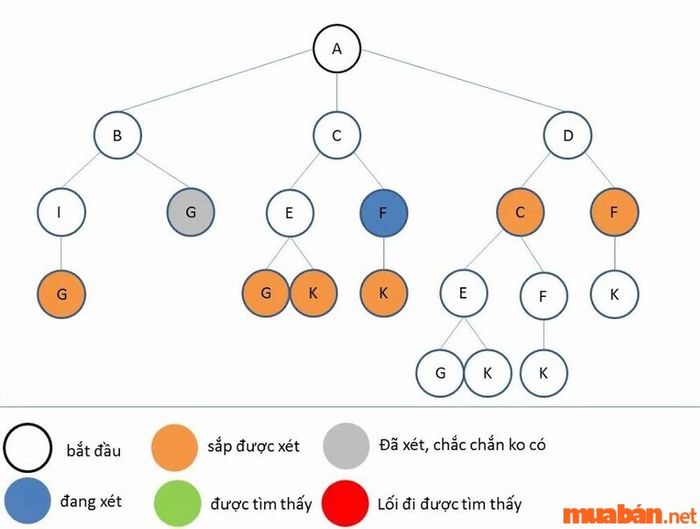 Thuật toán tìm kiếm
Thuật toán tìm kiếmThuật toán tìm kiếm được phát triển để kiểm tra hoặc truy xuất một phần tử từ bất kỳ cấu trúc dữ liệu nào mà nó được lưu trữ. Thuật toán này có thể áp dụng cho các dãy cấu trúc dữ liệu tuyến tính và cấu trúc dữ liệu đồ thị. Nó cũng được gọi là thuật toán tìm kiếm nhị phân và thường được sử dụng để tìm kiếm trong các tập dữ liệu đã được sắp xếp với độ phức tạp là hàm log N.
Cơ chế hoạt động của thuật toán tìm kiếm nhị phân là chia danh sách tìm kiếm thành hai nửa cho đến khi tìm thấy mục tiêu yêu cầu. Sau đó, nó sẽ thực hiện gỡ lỗi, đặc biệt là những lỗi liên quan đến git bisection.
3. Thuật toán sắp xếp
Thuật toán sắp xếp được sử dụng để tổ chức lại một mảng hoặc danh sách các phần tử dựa trên một toán tử so sánh cho các phần tử đó. Toán tử so sánh này sẽ quyết định thứ tự mới của các phần tử trong cấu trúc dữ liệu tương ứng. Chẳng hạn, danh sách các ký tự dưới đây sẽ được sắp xếp theo thứ tự tăng dần dựa trên giá trị ASCII của chúng. Nghĩa là, ký tự có giá trị ASCII thấp hơn sẽ đứng trước ký tự có giá trị cao hơn.
 Thuật toán sắp xếp
Thuật toán sắp xếpCác thuật toán sắp xếp cũng rất quan trọng trong các lĩnh vực phát triển nhanh chóng như trí tuệ nhân tạo (machine learning). Trong thời đại của dữ liệu lớn, khả năng lớn nhất của hệ thống công nghệ thông tin là làm việc với các tập dữ liệu khổng lồ. Điều này liên quan chặt chẽ đến quy trình phân loại. Trong lĩnh vực trí tuệ nhân tạo, nơi máy học từ những tập dữ liệu huấn luyện lớn, thuật toán sắp xếp mang lại nhiều lợi ích cho việc xây dựng và triển khai hệ thống AI.
Vì vậy, việc hiểu rõ các thuật toán sắp xếp cơ bản là rất cần thiết cho một số công việc liên quan đến khoa học máy tính. Nói chung, nhà khoa học máy tính cần phải là một nhà toán học – có hiểu biết về thuật ngữ và ngôn ngữ chuyên ngành của toán học và thống kê. Đồng thời, họ cần nắm vững cách sử dụng từng loại thuật toán sắp xếp một cách hiệu quả.
4. Thuật toán lập trình động
Thuật toán lập trình động (Kadane) là một công cụ được sử dụng để giải quyết những bài toán phức tạp liên quan đến trí tuệ nhân tạo. Nguyên tắc hoạt động là phân tách vấn đề lớn thành những bài toán con nhỏ hơn. Sau khi các bài toán này được giải quyết, Kadane sẽ đưa ra giải pháp cho vấn đề phức tạp ban đầu.
 Thuật toán lập trình động
Thuật toán lập trình động5. Thuật toán Dijkstra
Thuật toán Dijkstra là một trong những thuật toán kinh điển được phát triển để tìm kiếm đường đi ngắn nhất từ một điểm đã chỉ định tới tất cả các điểm khác trong một đồ thị có trọng số. Đây là cơ sở cho hầu hết các ứng dụng tìm kiếm đường đi và được sử dụng trong nhiều lĩnh vực, từ trí tuệ nhân tạo đến thiết kế game.
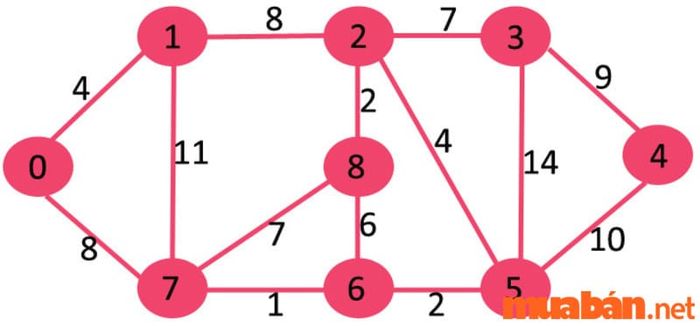 Thuật toán Dijkstra
Thuật toán Dijkstra6. Thuật toán phân tích liên kết
Thuật toán phân tích liên kết chủ yếu được áp dụng trong lĩnh vực mạng. Thuật toán này tạo ra mối tương quan trong cùng một tên miền với nhiều thực thể khác nhau. Phân tích liên kết sử dụng ma trận phức tạp và biểu đồ để kết nối các dữ liệu tương tự trong cùng một miền hiện tại. Loại thuật toán cơ bản này thường được áp dụng trong các công cụ như Google, Facebook và Twitter.
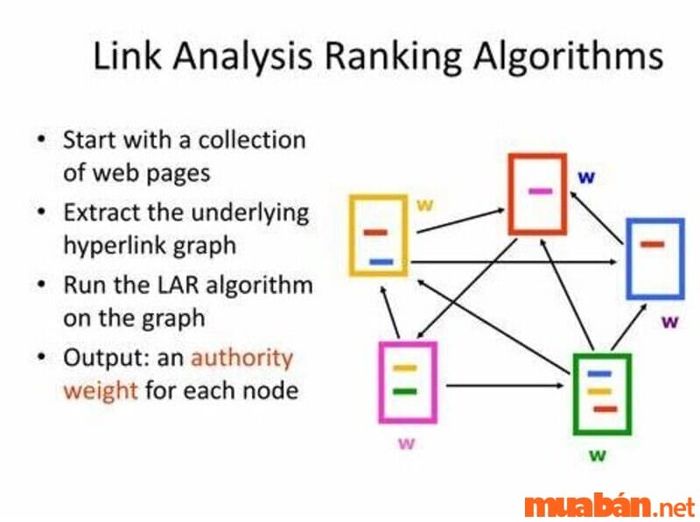 Thuật toán phân tích liên kết
Thuật toán phân tích liên kết7. Thuật toán Mô-đun
Nhiều thuật toán mã hóa phức tạp trở nên rất đơn giản khi được phân tích qua số học mô-đun. Trong số học mô-đun, chỉ các số nguyên được xử lý và các phép toán được áp dụng bao gồm cộng, trừ, nhân và chia. Tất cả các hoạt động trong số học mô-đun đều liên quan đến số nguyên dương.
 Thuật toán mô-đun
Thuật toán mô-đun8. Thuật toán phân tích cú pháp và chuỗi ký tự
Quy trình tạo ra chuỗi tương ứng luôn rất quan trọng, đặc biệt trong miền và các phần tử mạng. Thuật toán chuỗi ký tự phát huy hiệu quả cao trong những trường hợp cần khớp các chuỗi trong một dãy dài và xác nhận chuỗi thông qua phân tích cú pháp với các giới hạn đã được xác định. Loại thuật toán này thường được áp dụng trong phát triển web URL.
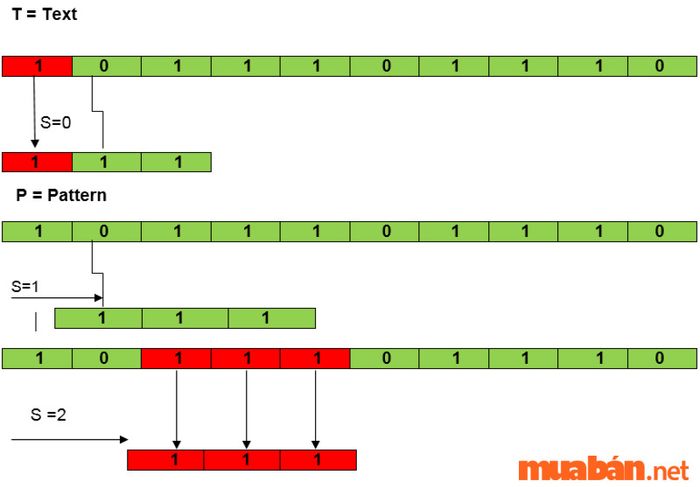 Thuật toán phân tích cú pháp và chuỗi ký tự
Thuật toán phân tích cú pháp và chuỗi ký tự9. Thuật toán biến đổi Fourier
Thuật toán biến đổi Fourier được coi là một thuật toán đơn giản nhưng rất hiệu quả. Nó được sử dụng để chuyển đổi tín hiệu từ miền thời gian sang miền tần số và ngược lại. Hiện nay, các mạng kỹ thuật số như wifi, internet, máy tính, điện thoại, bộ định vị và vệ tinh đều áp dụng thuật toán Fourier để hoạt động.
Biến đổi Fourier nhanh là một thuật toán dùng để tính toán biến đổi Fourier rời rạc của một dãy số hoặc nghịch đảo của nó. Phân tích Fourier giúp chuyển đổi tín hiệu từ miền gốc (thường là thời gian hoặc không gian) sang biểu diễn trong miền tần số và ngược lại. DFT được tạo ra bằng cách phân chia dãy giá trị thành các thành phần với tần số khác nhau.
 thuật toán là gì: Thuật toán Fourier
thuật toán là gì: Thuật toán Fourier[1] Biến đổi Fourier mang lại nhiều lợi ích trong nhiều lĩnh vực, nhưng việc tính toán trực tiếp từ định nghĩa thường quá chậm để áp dụng thực tế. Một thuật toán FFT giúp tính toán nhanh chóng các phép biến đổi này bằng cách phân tích ma trận DFT thành các thừa số thưa thớt (đa số là 0).
[2] Thuật toán này giảm độ phức tạp của việc tính toán DFT từ {\textstyle O\left(N^{2}\right)}{\textstyle O\left(N^{2}\right)}. Điều này xảy ra nếu chỉ đơn giản áp dụng định nghĩa DFT, cho {\textstyle O(N\log N)}{\textstyle O(N\log N)}, trong đó {\displaystyle N}N là kích thước dữ liệu.
Độ khác biệt về tốc độ có thể rất lớn, đặc biệt đối với các tập dữ liệu lớn, trong đó N có thể lên đến hàng nghìn hoặc triệu. Khi xảy ra lỗi làm tròn, nhiều thuật toán FFT chính xác hơn nhiều so với việc đánh giá trực tiếp hoặc gián tiếp định nghĩa DFT. Có nhiều thuật toán FFT khác nhau dựa trên nhiều lý thuyết đã được phát triển, từ số học số phức đơn giản đến lý thuyết nhóm và lý thuyết số.
10. Thuật toán mã hóa Huffman
Mã hóa Huffman là một thuật toán nén dữ liệu không mất thông tin. Trong thuật toán này, mỗi ký tự khác nhau được gán một mã có độ dài không cố định. Độ dài mã tương ứng với tần suất xuất hiện của các ký tự. Các ký tự thường gặp nhất sẽ có mã ngắn nhất, trong khi các ký tự ít phổ biến hơn sẽ có mã dài hơn.
Người sáng tạo đầu tiên của cây Huffman, cùng với người khác, sẽ duyệt qua cây để tìm mã tương ứng. Ví dụ: với chuỗi “YYYZXXYYX”, tần suất xuất hiện của ký tự Y cao hơn ký tự X, trong khi ký tự Z có tần suất thấp nhất. Do đó, mã cho Y sẽ ngắn hơn mã cho X, và mã cho X sẽ ngắn hơn mã cho Z. Độ phức tạp trong việc gán mã cho từng ký tự dựa trên tần suất của chúng là O(n log n).
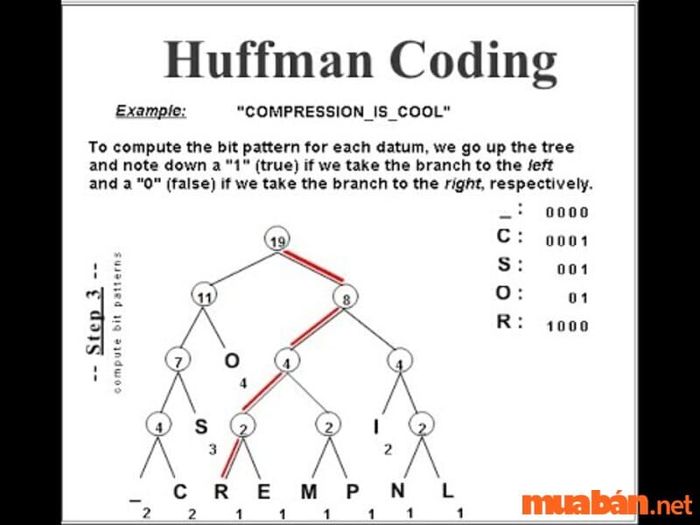 Huffman
Huffman11. Thuật toán các tập không giao nhau
Hai tập hợp được gọi là không giao nhau khi chúng không chia sẻ bất kỳ phần tử nào, tức là giao của chúng là tập rỗng. Cấu trúc dữ liệu lưu trữ các tập hợp không chồng chéo hoặc tách biệt của các phần tử được gọi là cấu trúc dữ liệu tập hợp rời rạc.
Cấu trúc dữ liệu tập hợp rời rạc hỗ trợ các thao tác sau: Thêm các tập hợp mới vào tập hợp rời rạc, hợp nhất các tập hợp rời rạc thành một tập hợp duy nhất thông qua thao tác Union, tìm đại diện cho một tập hợp rời rạc bằng thao tác Find, và kiểm tra xem hai tập hợp có thực sự không giao nhau hay không.
Chúng ta sẽ xem xét một tình huống với một số đối tượng và các nhiệm vụ sau sẽ được thực hiện đối với tập hợp không giao nhau: Thêm một mối quan hệ bạn bè mới, nghĩa là một người x trở thành bạn với người khác y, tức là thêm một phần tử mới vào tập hợp. Tìm hiểu xem cá nhân x có phải là bạn của cá nhân y (bạn trực tiếp hay gián tiếp) hay không.
 thuật toán là gì: Thuật toán các tập không giao nhau
thuật toán là gì: Thuật toán các tập không giao nhau12. Hệ số tích phân
Thuật toán lũy thừa số nguyên là một phương pháp toán học cung cấp các bước chi tiết để phân tích các thừa số nguyên tố của một số composite. Thuật toán này hữu ích trong việc giải quyết các vấn đề phức tạp trong các nền tảng mã hóa, nơi cần xử lý các số nguyên lớn phức tạp.
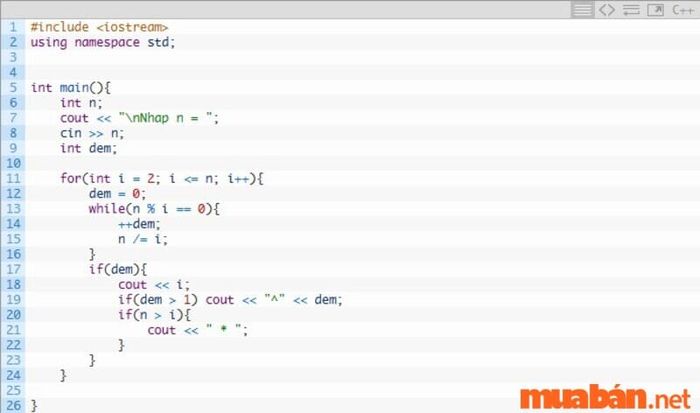 Cách thực hiện thuật toán lũy thừa số nguyên trong C++
Cách thực hiện thuật toán lũy thừa số nguyên trong C++