1. Tổng hợp và phân tích lực
1.1. Định nghĩa lực và cân bằng lực
Lực là gì?
Lực là một đại lượng véc tơ thể hiện sự tác động của một vật lên vật khác, dẫn đến việc vật bị gia tốc hoặc bị biến dạng.
Lực được mô tả bằng một mũi tên (véc-tơ)
- Gốc của mũi tên cho biết vị trí tác dụng của lực.
- Phương và chiều của mũi tên phản ánh phương và chiều của lực.
- Độ dài của mũi tên đại diện cho độ lớn của lực, theo tỷ lệ nhất định.
Khi nào thì hai lực được coi là cân bằng?
Hai lực cân bằng là hai lực tác động lên cùng một vật, cùng phương, cùng cường độ và ngược chiều nhau.
Đơn vị đo lực là gì?
Đơn vị đo lực là Niutơn (N).
Tổng hợp lực là gì?
Tổng hợp lực là quá trình thay thế các lực tác động đồng thời lên một vật bằng một lực duy nhất có tác dụng tương đương. Lực duy nhất này gọi là hợp lực.
Cách tìm hợp lực được gọi là phương pháp tổng hợp lực.
Các quy tắc tổng hợp lực
Quy tắc hình bình hành: Nếu hai lực đồng quy tạo thành hai cạnh của một hình bình hành, thì đường chéo từ điểm đồng quy biểu diễn hợp lực của chúng.
(1).jpg)
(Quy tắc hình bình hành trong vật lý lớp 10)
Tổng hợp ba lực F1→, F2→, và F3→
- Chọn hai cặp lực theo thứ tự ưu tiên: cùng chiều, ngược chiều, hoặc vuông góc để tổng hợp chúng thành một lực tổng hợp F12→
- Tiếp tục tổng hợp lực F12→ với lực F3→ còn lại để tìm ra lực tổng hợp cuối cùng F→
Công thức để tính tổng hợp lực
Theo công thức của quy tắc hình bình hành
F² = F1² + F2² + 2.F1.F2.cos(alpha)
1.2. Phân tích lực
Phân tích lực là gì?
Phân tích lực là quá trình thay thế một lực bằng hai hoặc nhiều lực có tác dụng tương đương. Các lực thay thế này được gọi là các lực thành phần.
Phân tích một lực thành hai lực thành phần trên hai phương đã cho
(1).jpg)
(Phân tích một lực thành hai lực thành phần theo hai phương đã cho)
Điều kiện để một chất điểm đạt trạng thái cân bằng
Để một chất điểm ở trạng thái cân bằng, hợp lực của tất cả các lực tác dụng lên nó phải bằng không.
(2).png)
Các dạng bài tập liên quan đến tổng hợp và phân tích lực
Tổng hợp các lực tác động lên một vật.
Cách giải:
- Nếu các lực có cùng phương và cùng chiều, thì lực tổng hợp sẽ là: F = F1 + F2 và có chiều giống như hai lực này.
- Nếu hai lực có cùng phương nhưng ngược chiều, lực tổng hợp sẽ là: F = |F1 - F2| và có chiều giống với lực có độ lớn lớn hơn.
- Nếu hai lực không cùng phương, lực tổng hợp sẽ được tính bằng: F² = F1² + 2F1.F2.cos(alpha) và có phương theo quy tắc hình bình hành.
2. Bài tập ứng dụng tổng hợp lực
LOẠI 1: TỔNG HỢP HAI LỰC
- Áp dụng quy tắc hình bình hành
- Áp dụng quy tắc khi hai lực có cùng phương và cùng chiều
- Áp dụng quy tắc khi hai lực có cùng phương nhưng ngược chiều
LOẠI 2: TỔNG HỢP BA LỰC
Bước 1: Chọn hai cặp lực theo thứ tự ưu tiên: cùng chiều, ngược chiều, hoặc vuông góc và tổng hợp chúng thành một lực duy nhất

Bước 2: Tiếp tục tổng hợp lực còn lại để xác định lực tổng hợp cuối cùng
Phương pháp: áp dụng quy tắc hình bình hành

Bài 1: Cho hai lực đồng quy có độ lớn lần lượt là 4 (N) và 5 (N), hợp thành một góc alpha. Tính góc alpha nếu hợp lực của hai lực này có độ lớn là 7,8 (N)
Hướng dẫn giải:
F1 = 4 N
F2 = 5 N
Hợp lực F = 7,8 N
Tính góc alpha
Áp dụng công thức quy tắc hình bình hành:
F² = F1² + F2² + 2.F1.F2.cos(alpha)
Tính được góc alpha = 60°15'
Bài 2: Ba lực đồng quy nằm trên cùng một mặt phẳng, mỗi lực có độ lớn F1 = F2 = F3 = 20 N, và mỗi cặp lực hợp với nhau một góc 120°. Tính độ lớn của hợp lực của chúng.
Hướng dẫn giải:
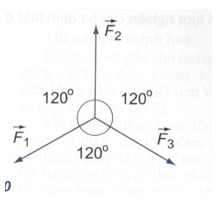
Hợp lực F → = F1 → + F2 → + F3 →
Hoặc F → = F1 → + F23 →
Theo hình vẽ, F23 có độ lớn F23 = 2F2.cos(60°) = F1
Do F23 cùng phương nhưng ngược chiều với F1, nên Fhl = 0
Bài 3: Tính hợp lực của hai lực đồng quy với F1 = 16 N và F2 = 12 N, khi góc giữa hai lực lần lượt là alpha = 0°; 60°; 120°; 180°. Xác định góc hợp lực để lực tổng hợp có độ lớn 20 N.
Hướng dẫn giải:
F² = F1² + F2² + 2.F1.F2.cos(alpha)
Khi góc alpha = 0°, lực tổng hợp F = 28 N
Khi góc alpha = 60°, lực tổng hợp F = 24,3 N
Khi góc alpha = 120°, lực tổng hợp F = 14,4 N
Khi góc alpha = 180°, lực tổng hợp F = F1 - F2 = 4 N
Khi F = 20 N, thì góc alpha = 90°
Bài 4: Một vật nằm trên mặt phẳng nghiêng 30° so với phương ngang, chịu tác dụng của trọng lực 50 N. Tính độ lớn các thành phần của trọng lực theo hai phương vuông góc và song song với mặt nghiêng.
Hướng dẫn giải:
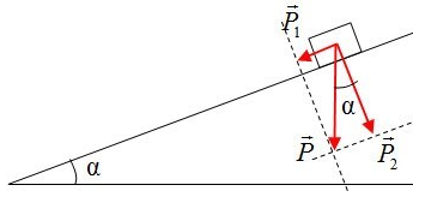
P1 = P.sin(alpha) = 25 N
P2 = P.cos(alpha) = 25√3 N
Bài 5: Một lực F có độ lớn 100 N, tạo với trục Ox góc 36,87° và với trục Oy góc 53,13°. Xác định độ lớn các thành phần của lực F trên các trục Ox và Oy.
Hướng dẫn giải:
36,87° = 53,13° = 90°
Fx = F.cos(36,87°) = 80 N
Fy = F.sin(53,13°) = 60 N
Bài 5: Một lực F có độ lớn 100 N, tạo với trục Ox góc 36,87° và với trục Oy góc 53,13°. Xác định độ lớn các thành phần của lực F theo trục Ox và Oy.
Hướng dẫn giải:
36,87° + 53,13° = 90°. Fx = F.cos(36,87°) = 80 N; Fy = F.sin(53,13°) = 60 N
Bài 6: Cho hai lực F1 = 6 N và F2 = 8 N. Tính độ lớn hợp lực của F1 và F2 trong các trường hợp góc kẹp giữa chúng như sau:
a. α = 0°
b. α = 180°
c. α = 90°
d. α = 120°
e. α = 60°
f. α = 30°
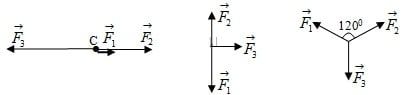
Bài 7: Cho ba lực đồng phẳng như trong hình vẽ, xác định độ lớn của hợp lực F và vẽ hình minh họa.
a. F1 = 1 N; F2 = 3 N; F3 = 5 N
b. F1 = 7 N; F2 = 4 N; F3 = 3 N
c. F1 = F2 = F3 = √3 N; các góc giữa các lực đều là 120°
Bài 8: Hai lực F1 = 9 N và F2 = 4 N tác dụng vào một vật. Xác định hợp lực của hai lực này.
a. 2 N
b. 4 N
c. 6N
d. 15N
LOẠI 3: SỰ CÂN BẰNG LỰC (thường xuất hiện trong các bài kiểm tra)
a. Các lực cân bằng: Các lực này khi tác động đồng thời lên một vật sẽ không làm vật thay đổi vận tốc.
b. Điều kiện cân bằng của điểm vật
ĐỀ BÀI VỀ CÂN BẰNG LỰC VÀ CÁC PHƯƠNG PHÁP GIẢI QUYẾT
.jpg)
