Khám phá sức mạnh số nguyên tố trong chương trình toán học. Tìm hiểu về bảng số nguyên tố, dãy số nguyên tố và siêu nguyên tố.
Bí mật của số nguyên tố
Số nguyên tố là tập hợp các số lớn hơn 1 chỉ chia hết cho nó và 1. Ví dụ: 3 chỉ chia hết cho 1 và nó. Các số như 11, 13, 17, 19,... đều là số nguyên tố.
 Khám phá sức mạnh số nguyên tố: Bảng và ví dụ
Khám phá sức mạnh số nguyên tố: Bảng và ví dụ
Đặc điểm quan trọng của số nguyên tố
Đặc tính nổi bật của số nguyên tố:
- Không bao gồm số 1.
- Các số nguyên tố đều không chia hết cho 2 trừ số 2.
- Dãy số nguyên tố là vô hạn và không có giới hạn tương tự như tập N.
- Ước bé nhất của số bất kỳ thuộc tập N luôn là số nguyên tố. Ví dụ: 15 chia hết cho 3 (ước nhỏ nhất), 3 là số nguyên tố.
- Số X có ước nhỏ nhất là số dương, khác 1 và nhỏ hơn căn bậc hai của X thì đó chính là số nguyên tố. Ví dụ: 30 có ước nhỏ nhất là 5, tính chất của 5 khác 1 và nhỏ hơn căn bậc 2 của 30, nên 5 là số nguyên tố.
 Tính chất cơ bản của số nguyên tố: Số 2 là số nguyên tố duy nhất là số chẵn.
Tính chất cơ bản của số nguyên tố: Số 2 là số nguyên tố duy nhất là số chẵn.
Bảng số nguyên tố trong toán học
Dãy số nguyên tố không có giới hạn cụ thể vì tính chất vô hạn của số tự nhiên. Tuy nhiên, vẫn có những số phổ biến được sử dụng. Dưới đây là bảng số nguyên tố với các số bé hơn 1000:

| 2 | 79 | 191 | 311 | 439 | 577 | 709 | 857 |
| 3 | 83 | 193 | 313 | 443 | 587 | 719 | 859 |
| 5 | 89 | 197 | 317 | 449 | 593 | 727 | 863 |
| 7 | 97 | 199 | 331 | 457 | 599 | 733 | 877 |
| 11 | 101 | 211 | 337 | 461 | 601 | 739 | 881 |
| 13 | 103 | 223 | 347 | 463 | 607 | 743 | 883 |
| 17 | 107 | 227 | 349 | 467 | 613 | 751 | 887 |
| 19 | 109 | 229 | 353 | 479 | 617 | 757 | 907 |
| 23 | 113 | 233 | 359 | 487 | 619 | 761 | 911 |
| 29 | 127 | 239 | 367 | 491 | 631 | 769 | 919 |
| 31 | 131 | 241 | 373 | 499 | 641 | 773 | 929 |
| 37 | 137 | 251 | 379 | 503 | 643 | 787 | 937 |
| 41 | 139 | 257 | 383 | 509 | 647 | 797 | 941 |
| 43 | 149 | 263 | 389 | 521 | 653 | 809 | 947 |
| 47 | 151 | 269 | 397 | 523 | 659 | 811 | 953 |
| 53 | 157 | 271 | 401 | 541 | 661 | 821 | 967 |
| 59 | 163 | 277 | 409 | 547 | 673 | 823 | 971 |
| 61 | 167 | 281 | 419 | 557 | 677 | 827 | 977 |
| 67 | 173 | 283 | 421 | 563 | 683 | 829 | 983 |
| 71 | 179 | 293 | 431 | 569 | 691 | 839 | 991 |
| 73 | 181 | 307 | 433 | 571 | 701 | 853 | 997 |
Bài tập thực hành về số nguyên tố
Để hiểu rõ hơn về số nguyên tố và các khái niệm như bảng, dãy số nguyên tố, hãy tham khảo những bài tập sau đây:
Bài tập phân tích thừa số nguyên tố
Phân tích thừa số nguyên tố là quá trình tìm con số không thể chia hết cho ước chung nhỏ nhất. Xem xét số A, kiểm tra chia hết cho 2, sau đó 3, 5,... trên bảng số nguyên tố. Cuối cùng, lấy các thừa số và nhân cho nhau.

Ví dụ: Phân tích số 140 thành thừa số nguyên tố, chia 140 cho 2 được 70. Tiếp tục chia 70 cho 2 được 35. 35 chia cho 5 là 7, số này chỉ chia hết cho 1 và chính nó. Thừa số nguyên tố: 140 = 2 x 2 x 5 x 7 x 1.
Bài tập tìm ước số chung lớn nhất
Trong bài toán tìm ước chung lớn nhất, số được cho có nhiều ước chung (ký hiệu là ƯCLN(a,b)). Giải bằng cách lập tích các thừa số nguyên tố và lấy số mũ nhỏ nhất.
Ví dụ, bài toán yêu cầu tìm ước chung lớn nhất của số 120 và 80. Phân tích như sau: 80 = 2^4 x 5 và 120 = 2^3 x 3 x 5.
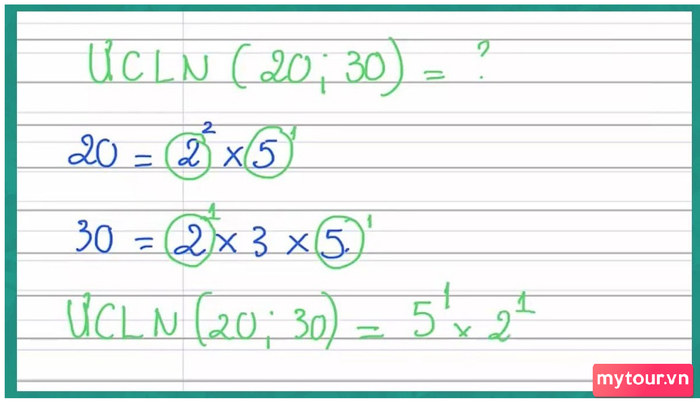
Kết quả thấy ước chung của 120 và 80 là 2 và 5. Phân tích số mũ, 2 có số mũ nhỏ nhất là 3, 5 có số mũ nhỏ nhất là 1. ƯCLN (80, 120) = 2^3 x 5 = 40.
Một số định nghĩa khác
Ngoài các khái niệm cơ bản về số nguyên tố là gì, hãy tìm hiểu thêm về số nguyên tố cùng nhau, số siêu nguyên tố, và tính chất của số 1, 2.
1, 2 có phải số nguyên tố không?
Theo định nghĩa, số lớn hơn 1 và không chia hết cho số nào ngoài chính nó được coi là số nguyên tố. Trong hai số 1 và 2, chỉ có số 2 thỏa điều kiện số nguyên tố.
 Số 1 không thuộc dãy số nguyên tố
Số 1 không thuộc dãy số nguyên tố
Số nguyên tố cùng nhau là gì?
Số nguyên tố cùng nhau khi số lớn nhất mà cả hai cùng chia hết là 1. Ví dụ 2 và 3 là số nguyên tố cùng nhau vì chỉ chia hết cho 1. Hoặc 18 và 54 không là số nguyên tố cùng nhau vì chia hết cho 9.

Số siêu nguyên tố là gì?
Số siêu nguyên tố là số khi thêm chữ số bên cạnh vẫn là số nguyên tố. Ví dụ 73 là số nguyên tố, thêm số 3 là 733 vẫn là số nguyên tố. Thêm số 7, dạng số 7337 vẫn là số nguyên tố.
Kiến thức cơ bản về số nguyên tố là gì, cùng một số dạng toán phổ biến liên quan đến bảng, dãy số nguyên tố, siêu nguyên tố. Hi vọng bạn có thể áp dụng trong học tập. Để biết thêm về toán học, đọc các bài sau trên Mytour.
- Khám phá thêm: Thuật ngữ chuyên ngành, ngôn ngữ công nghệ
