1. Dao động điều hòa là gì?
Dao động điều hòa là loại dao động cơ học, trong đó vật chuyển động qua lại quanh một vị trí cân bằng (thường là vị trí đứng yên của vật). Ví dụ gồm dao động của thuyền neo tại chỗ, chuyển động đung đưa của chiếc lá, hoặc dây đàn rung khi nghệ sỹ chơi đàn.
Dao động điều hòa có quỹ đạo là đoạn thẳng và li độ của vật được mô tả bằng hàm cos (hoặc sin) theo thời gian.
Đồ thị của dao động điều hòa có dạng đường hình sin, vì thế dao động điều hòa còn được gọi là dao động hình sin.
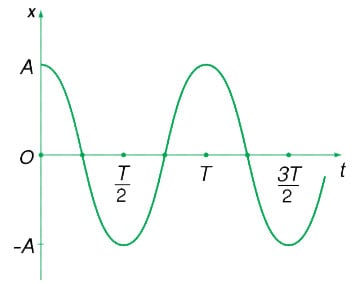
Ví dụ về dao động điều hòa: Một điểm dao động điều hòa trên đoạn thẳng có thể xem như hình chiếu của một điểm đang chuyển động tròn đều lên đoạn thẳng đó, như trong hình minh họa.
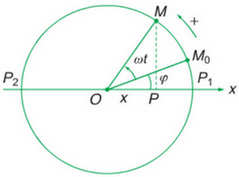
- Giả sử tại thời điểm t = 0, điểm M ở vị trí M được xác định bởi góc φ.
Tại thời điểm t, vị trí của điểm M được xác định bởi (ωt + φ).
Lúc này, tọa độ x của hình chiếu P của M trên đoạn thẳng OP có phương trình như sau:
x = OM.cos(ωt + φ)
- Nếu đặt OM = A, phương trình tọa độ x trở thành:
x = A.cos(ωt + φ)
Trong đó, A, ω, và φ là các hằng số.
Vì hàm sin và cos đều là hàm điều hòa, nên dao động của điểm P được gọi là dao động điều hòa.
2. Phương trình động lực học của dao động điều hòa đơn giản
2.1. Phương trình li độ
Phương trình li độ thường có dạng chuẩn như sau:
x = A.cos(ωt + φ)
Trong đó:
A, ω, φ là các hằng số xác định dao động.
x: li độ của vật, đo bằng mét (m) hoặc xăng-ti-mét (cm).
A: biên độ của dao động (giá trị cực đại của li độ), đo bằng mét (m) hoặc xăng-ti-mét (cm).
ω: tần số góc của dao động, đo bằng rad/s.
φ: pha ban đầu của dao động, đo bằng rad.
(ωt + φ): pha của dao động tại thời điểm t, hay còn gọi là pha li độ, đo bằng rad.
2.2. Chu kỳ
Chu kỳ của dao động điều hòa là thời gian cần thiết để vật thực hiện một chu kỳ đầy đủ (hoặc thời gian ngắn nhất để vật thực hiện một dao động hoàn chỉnh), ký hiệu T, đo bằng giây (s).
Công thức liên hệ giữa chu kỳ và tần số góc là T = 2π / ω
2.3. Tần số
Tần số là số lần dao động toàn phần mà vật thực hiện trong một giây, là nghịch đảo của chu kỳ, ký hiệu f, đo bằng Hertz (Hz).
Công thức liên hệ giữa tần số và chu kỳ là: f = 1 / T
Công thức liên hệ giữa tần số và tần số góc là: f = ω / 2π
2.4. Vận tốc
Vận tốc trong dao động điều hòa là đạo hàm của li độ x theo thời gian t:
v = x' = -ωA.sin(ωt + φ)
Vận tốc là một đại lượng dao động điều hòa:
- Tại các vị trí biên x = +A hoặc x = -A, vận tốc bằng 0
- Tại vị trí cân bằng x = 0, vận tốc đạt giá trị cực đại v = Aω
Trong dao động điều hòa, vì vận tốc v và li độ x vuông pha nhau, nên chúng có mối quan hệ độc lập, được chứng minh qua việc bình phương tỉ số x/A và cộng với bình phương của tỉ số v / vmax.
(x/A)^2 + (v / vmax)^2 = 1
<=> A^2 = x^2 + (v / ω)^2
2.5. Gia tốc
Gia tốc trong dao động điều hòa là đạo hàm bậc hai của li độ x theo thời gian, tương đương với đạo hàm của vận tốc: a = x''
Dù phương trình li độ có dạng sin hay cos, mối quan hệ giữa gia tốc và li độ luôn là:
a = v' = -ω^2.x = -ω^2.A.cos(ωt + φ)
Như vậy:
- Tại vị trí cân bằng x = 0, gia tốc a = 0 và lực tổng hợp F = 0
- Gia tốc trong dao động điều hòa luôn ngược pha (đối pha) với li độ, tức là sớm pha π/2 so với vận tốc.
- Gia tốc trong dao động điều hòa đạt giá trị cực đại khi vật ở một trong hai vị trí biên (x = +A hoặc x = –A). Vì gia tốc a cũng vuông pha với vận tốc v, nên giữa a và v có mối quan hệ độc lập như sau:
(v / vmax)^2 + (a / a max)^2 = 1
2.6. Cơ năng dao động
Cơ năng của một chất điểm dao động điều hòa được bảo toàn (không thay đổi) và tỷ lệ với bình phương biên độ dao động của vật, ký hiệu W, đo bằng Jun (J).
W = Wt + Wđ = 1/2.k.A^2 = 1/2.m.ω^2 . A^2
Cụ thể là:
Wt biểu thị thế năng, có giá trị Wt = 1/2.k.x^2
Wđ biểu thị động năng, có giá trị Wđ = 1/2.m.v^2
2.7. Lực kéo hồi phục
Lực kéo tác động lên vật dao động điều hòa được tính theo công thức sau:
Fkv = m.a
Trong đó:
a đại diện cho gia tốc của vật, đơn vị tính là m/s²
m đại diện cho khối lượng của vật, đơn vị tính là kg
Fkv là đại lượng đại số với đơn vị đo là Jun (J)
3. Các bài tập ứng dụng về dao động điều hòa
Bài tập 1: (Xem Bài 6 trang 8 Sách giáo khoa Vật lý 12) Một vật dao động điều hòa theo phương trình x = Acos(ωt + φ).
a) Xác định công thức tính vận tốc và gia tốc của vật.
b) Tại các vị trí nào vận tốc bằng 0? Gia tốc bằng 0 ở đâu?
c) Vận tốc đạt độ lớn cực đại ở vị trí nào? Gia tốc đạt giá trị cực đại ở đâu?
Hướng dẫn giải:
a) Công thức tính vận tốc là v = x'(t) = -ωAsin(ωt + φ)
Gia tốc được tính theo công thức a = v'(t) = -ω².Acos(ωt + φ) hay a = -ω².x
b) Vận tốc v = 0 tại các vị trí biên x = A hoặc x = -A.
Tại điểm cân bằng x = 0, gia tốc a là 0.
Tại điểm cân bằng x = 0, vận tốc v bằng ωA.
Tại các vị trí biên x = A hoặc x = -A, gia tốc a bằng ω^2.A.
Bài tập 2: (Bài 7 trang 9 Sách giáo khoa Vật lý 12) Một vật dao động điều hòa có quỹ đạo dài 12cm. Biên độ của dao động này là bao nhiêu?
A. 12cm; B. – 12cm; C. 6cm; D. – 6cm;
Bài tập 3: (Bài 9 trang 9 Sách giáo khoa Vật Lý 12) Xét phương trình dao động điều hòa x = - 5cos(4πt) (cm). Xác định biên độ và pha ban đầu của dao động.
A. 5cm; 0 rad;
B. 5 cm; 4π rad;
C. 5 cm; (4π.t) rad;
D. 5cm; π rad;
Hướng dẫn giải:
Chọn Đáp án: D. 5 cm; π rad;
- Đặt phương trình x = -5cos(4πt) = 5cos(4πt + π) - Biên độ dao động là A = 5cm.
- Pha ban đầu của dao động là φ = π (rad)
Bài tập 4: (Bài 10 trang 9 Sách giáo khoa Vật lý 12) Phương trình dao động điều hòa là x = 2cos(5t - π/6)(cm). Xác định biên độ, pha ban đầu và pha tại thời điểm t của dao động.
Hướng dẫn giải:
- Biên độ dao động là A = 2 (cm)
- Pha ban đầu của dao động là φ = -π/6 (rad)
- Pha của dao động tại thời điểm t là 5t - π/6 (rad)
Bài tập 5: (Bài 11 trang 9 Sách giáo khoa Vật lý 12) Một vật dao động điều hòa cần 0,25s để di chuyển từ một điểm có vận tốc bằng không đến điểm tiếp theo tương tự. Khoảng cách giữa hai điểm này là 36cm. Tính toán:
a) Chu kỳ b) Tần số c) Biên độ.
Hướng dẫn giải:
a) Vận tốc của vật dao động điều hòa bằng 0 tại hai điểm biên.
=> Khi vật di chuyển từ một điểm có vận tốc bằng không đến điểm tiếp theo cũng có vận tốc bằng không, điều này có nghĩa là vật di chuyển từ một biên này đến biên kia trong thời gian bằng nửa chu kỳ.
- Ta có t = T/2 và t = 0,25 (s) => T = 2.t = 2.0,25 = 0,5 (s).
b) Tần số dao động được tính là f = 1/T = 2 Hz
c) Biên độ dao động là A = L/2 = 18 cm.
Trên đây là bài viết của Mytour về dao động điều hòa. Mong rằng bài viết đã cung cấp những kiến thức hữu ích cho quý độc giả. Cảm ơn quý vị đã theo dõi.
