Khám phá diện tích hình tròn, hình quạt tròn và phương pháp giải bài tập chi tiết

Buzz

Nội dung bài viết

1. Công thức tính diện tích hình tròn và hình quạt tròn

2. Các dạng bài tập về diện tích hình tròn và hình quạt tròn

3. Bài tập về tính diện tích hình tròn và hình quạt tròn

Xem thêm

Tài liệu về diện tích hình tròn, hình quạt tròn cùng với hướng dẫn giải bài tập chi tiết được Mytour biên soạn nhằm hỗ trợ học sinh ôn tập và nghiên cứu hiệu quả hơn

1. Công thức tính diện tích hình tròn và hình quạt tròn

Công thức tính diện tích hình tròn

Diện tích hình tròn chính là phần không gian nằm bên trong đường tròn, và việc tính toán diện tích này đã được các nhà toán học Hy Lạp cổ đại nghiên cứu từ thế kỷ trước Công nguyên. Họ nhận ra rằng diện tích của hình tròn có mối liên hệ trực tiếp với bình phương bán kính của nó. Điều này có nghĩa là với bán kính của hình tròn, bạn có thể tính diện tích một cách đơn giản nhờ vào công thức cụ thể. Khám phá này đã mở ra những cơ hội mới trong nghiên cứu hình học và toán học, và vẫn giữ vai trò quan trọng trong học thuật cũng như ứng dụng hiện đại.

Diện tích S của một hình tròn với bán kính R được tính bằng công thức

$\Pi R^{2}$

Công thức tính diện tích hình quạt tròn

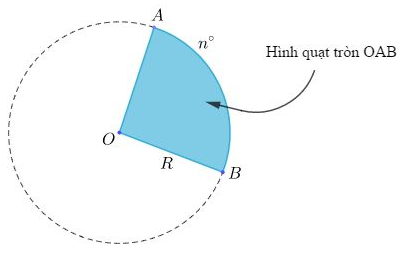
Diện tích của hình quạt tròn, hay còn gọi là diện tích phần quạt của hình tròn, là một khái niệm quan trọng trong hình học và toán học. Để hình dung, hãy tưởng tượng một hình tròn với trung tâm và đường viền hoàn chỉnh. Để tạo hình quạt tròn, chúng ta chọn hai điểm bất kỳ trên đường viền của hình tròn và nối chúng với trung tâm của hình tròn.

Diện tích của phần hình tròn giữa hai tia này chính là diện tích hình quạt tròn. Để tính toán, chúng ta cần biết góc giữa hai tia, đo bằng độ (°), vì đây là yếu tố chính xác xác định diện tích hình quạt. Diện tích hình quạt tròn là phần diện tích của hình tròn toàn bộ mà hai tia này bao phủ.

Tính diện tích của hình quạt tròn bằng cách nhân tỉ lệ góc giữa hai tia với diện tích toàn phần của hình tròn là một khía cạnh quan trọng trong toán học và hình học. Phương pháp này làm nổi bật mối quan hệ giữa góc và diện tích, cho thấy sự tương tác tinh vi giữa các yếu tố trong các hình dạng hình học.

Trong một hình quạt tròn, góc giữa hai tia là yếu tố chính xác quyết định diện tích của nó. Khi góc tăng, diện tích hình quạt tròn cũng tăng theo, và khi góc giảm, diện tích giảm. Điều này cho phép so sánh và đánh giá mức độ mở rộng của các hình quạt tròn dựa trên góc của chúng.

Khả năng tính diện tích hình quạt tròn bằng cách sử dụng góc và diện tích toàn phần của hình tròn mang lại công cụ hữu ích trong nhiều ứng dụng thực tế, từ kỹ thuật đến khoa học tự nhiên và địa lý. Điều này giúp chúng ta hiểu không gian và hình dạng xung quanh, tối ưu hóa thiết kế và tính toán trong các lĩnh vực khác nhau. Hiểu rõ mối liên hệ giữa góc và diện tích là thiết yếu cho sự phát triển và ứng dụng của toán học và khoa học.

Diện tích của hình quạt tròn với bán kính R và góc n° được tính bằng công thức:

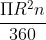
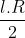
$\frac{\Pi R^{2}n}{360}$ $\frac{l.R}{2}$

(với l là độ dài của cung hình quạt tròn).

Khám phá diện tích hình tròn, diện tích hình quạt tròn và phương pháp giải bài tập chi tiết

2. Các dạng bài tập về diện tích hình tròn và hình quạt tròn

Dạng 1: Tính diện tích hình tròn và hình quạt tròn

Cách giải: Sử dụng công thức để tính diện tích hình tròn và hình quạt tròn.

Ví dụ 1: Điền vào ô trống trong bảng dưới đây (làm tròn đến một chữ số thập phân).

Bán kính đường tròn	Độ dài đường tròn	Diện tích hình tròn	Số đo của cung tròn n°	Diện tích hình quạt tròn cung n°
	12cm		45°
2cm				10,5cm2
		40cm2	10cm2

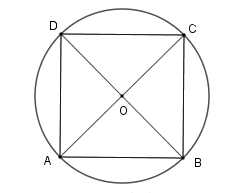
Ví dụ 2: Cho hình vuông có cạnh 5 cm nội tiếp trong đường tròn (O). Tính chiều dài đường tròn (O) và diện tích của hình tròn (O).

Khám phá diện tích hình tròn, hình quạt tròn và phương pháp giải bài tập chi tiết

Dạng 2: Tính diện tích của các hình đặc biệt liên quan đến hình tròn và hình quạt tròn

Cách giải: Chia hình cần tính thành các phần nhỏ hơn với công thức tính diện tích riêng biệt và áp dụng công thức để tính.

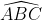
$\widehat{ABC}$

3. Bài tập về tính diện tích hình tròn và hình quạt tròn

Bài 1: Cho hình vuông có cạnh dài 10 cm. Tính chu vi và diện tích của đường tròn nội tiếp trong hình vuông.

Bài 2: Một hình quạt có chu vi 28 cm và diện tích 49 cm². Tính bán kính của hình quạt tròn đó.

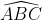
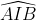
$\widehat{ABC}$ $\widehat{AIB}$

a) Chiều dài cung nhỏ AB.

b) Diện tích của hình quạt được giới hạn bởi cung nhỏ AB và hai bán kính IA, IB.

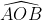
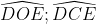
$\widehat{AOB}$ $\widehat{DOE}; \widehat{DCE}$

b) Tính chu vi của đường tròn (O; R) và đường tròn (O; r); chiều dài cung DE.

b) Tính diện tích của hình tròn (O; r) và diện tích hình quạt tròn DOE.

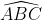
$\widehat{ABC}$

Bài 7: Cho đường tròn (O) với đường kính AB. Điểm M nằm trên đoạn AB. Vẽ dây CD vuông góc với AB tại M. Biết rằng AM = 2 cm và CD = 43 cm. Tính:

a) Tính chu vi của đường tròn (O) và diện tích của hình tròn (O).

Bài 8: Cho đường tròn (O; R) với đường kính AB cố định. M là trung điểm của đoạn OB. Dây CD vuông góc với AB tại M. Điểm E di chuyển trên cung lớn CD (E khác A). Kết nối AE cắt CD tại K, và BE cắt CD tại H.

a) Chứng minh rằng các điểm B, M, E, K nằm trên cùng một đường tròn.

b) Chứng minh rằng tích AE.AK là hằng số.

c) Tính diện tích hình quạt được giới hạn bởi OB, OC và cung nhỏ BC theo R.

Bài 9: Cho nửa đường tròn (O; R) với đường kính AB. Vẽ dây CD = R (với C nằm trên cung AD). Kết nối AC và BD để chúng cắt nhau tại M.

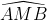
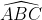
$\widehat{AMB}$ $\widehat{ABC}$

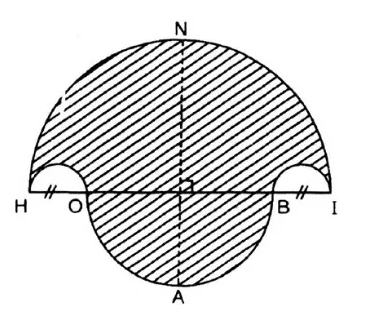
Bài 10: Cho hình vẽ gồm các cung tròn của các đường tròn với bán kính khác nhau xếp nối tiếp. Tính diện tích phần gạch chéo trong hình vẽ với HI = 10 cm; HO = BI = 2 cm.

Bài tập 11: Tính bán kính của hình tròn với chu vi C = 16,328 dm và C = 8,792 cm.

Bài tập 12: Tính chu vi và diện tích của hình tròn với các thông số sau:

a) r = 5 cm; r = 0,8 cm; r = 4/5 dm

b) d = 5,2 m; d = 1,2 m; d = 3/5 dm

Bài tập 13: Một cái nong hình tròn có chu vi là 376,8 cm. Tính diện tích của cái nong đó theo đơn vị mét vuông.

Bài tập 14: Sân trường của bạn Hoa có hình chữ nhật với chiều dài 45 m và chiều rộng kém chiều dài 6,5 m. Chính giữa sân là một bồn hoa hình tròn có đường kính 3,2 m. Tính diện tích còn lại của sân sau khi trừ bồn hoa.

Bài tập 15: Trong sân trường có hai bồn hoa hình tròn. Bồn hoa cúc có đường kính 40 dm, còn bồn hoa hồng có chu vi 9,42 m. Tìm bồn hoa nào có diện tích lớn hơn và chênh lệch diện tích là bao nhiêu dm².

Bài tập 16:

a) Một mặt bàn ăn hình tròn có chu vi 4,082 m. Tính bán kính của mặt bàn này.

b) Một biển báo giao thông hình tròn có chu vi 1,57 m. Tính đường kính của biển báo.

Bài tập 17: Một bánh xe ô tô có bán kính 0,25 m. Hãy tính:

a) Đường kính của bánh xe là bao nhiêu mét?

b) Chu vi của bánh xe là bao nhiêu mét?

Bài tập 18: Một hình tròn có chu vi 254,24 dm. Tính đường kính và bán kính của hình tròn đó.

Bài tập 19: Một hình tròn có bán kính bằng cạnh của một hình vuông có chu vi 25 cm. Tính chu vi của hình tròn đó.

Bài tập 20: Cho hình tròn tâm O với đường kính AB = 8 cm.

a) Tính chu vi của hình tròn tâm O, đường kính AB; hình tròn tâm M với đường kính OA; và hình tròn tâm N với đường kính OB.

b) So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi của hình tròn tâm O.

Các câu hỏi thường gặp

Công thức nào được sử dụng để tính diện tích hình tròn?

Công thức tính diện tích hình tròn là S = πR², trong đó S là diện tích và R là bán kính của hình tròn. Công thức này thể hiện mối liên hệ giữa diện tích và bán kính, giúp học sinh dễ dàng tính toán.

Diện tích của hình quạt tròn được tính như thế nào?

Diện tích hình quạt tròn được tính bằng công thức S = (θ/360) * πR², với θ là góc của hình quạt và R là bán kính. Công thức này cho phép xác định diện tích dựa trên tỉ lệ giữa góc và toàn bộ hình tròn.

Có những dạng bài tập nào liên quan đến diện tích hình tròn?

Các dạng bài tập về diện tích hình tròn thường bao gồm tính diện tích hình tròn, diện tích hình quạt tròn và các bài toán liên quan đến hình đặc biệt. Điều này giúp học sinh thực hành và củng cố kiến thức.

Tại sao việc hiểu công thức tính diện tích hình tròn lại quan trọng?

Việc hiểu công thức tính diện tích hình tròn rất quan trọng vì nó là nền tảng cho nhiều khái niệm toán học khác. Nó không chỉ áp dụng trong học tập mà còn trong các lĩnh vực kỹ thuật và khoa học thực tiễn.

Nội dung từ Mytour nhằm chăm sóc khách hàng và khuyến khích du lịch, chúng tôi không chịu trách nhiệm và không áp dụng cho mục đích khác.

Nếu bài viết sai sót hoặc không phù hợp, vui lòng liên hệ qua email: [email protected]