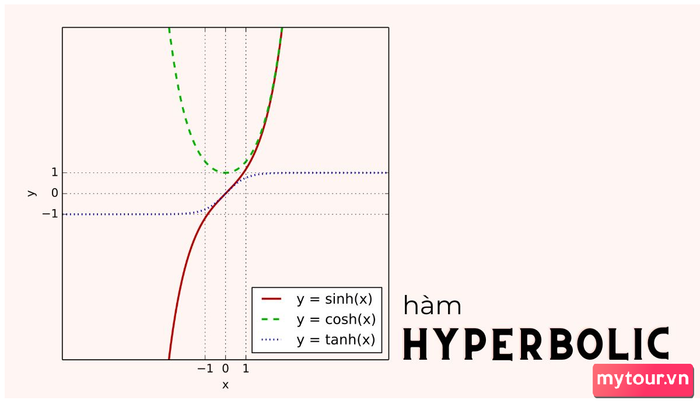
Độ Sâu trong Hàm Hyperbolic
Hàm Hyperbol chức năng tương tự như hàm số lượng giác. Nếu hàm số lượng giác được biểu diễn trên đường tròn với đơn vị chuẩn, thì Hyperbolic lại xuất hiện dưới dạng các đường Hyperbol.
Thêm vào đó, theo quan điểm Logarit học, Hàm Hyperbolic là phân thức của ex với điều kiện tử và mẫu số có bậc không lớn hơn 2.
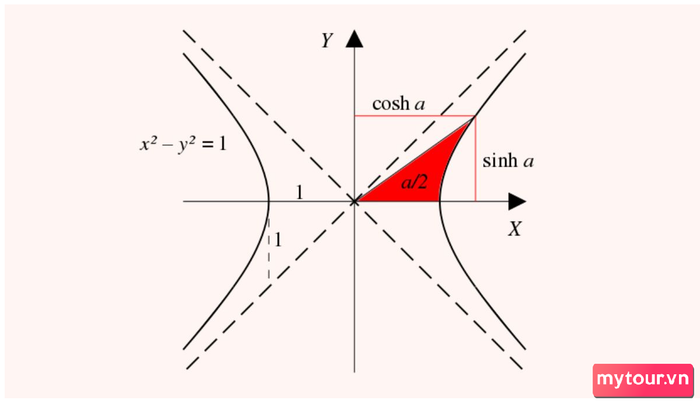
Công Thức Đặc Sắc của Hàm Hyperbolic
Hàm Hyperbolic là một khám phá tuyệt vời với những định lý như sin hyperbolic - kí hiệu: sinh; cosin hyperbolic - ký hiệu - cosh và hàm tang hyperbolic - ký hiệu tanh. Bằng cách sử dụng 3 công thức cơ bản, chúng ta có thể tạo ra những hàm số phức tạp như cotang hyperbol - ký hiệu coth, sec hyperbol - ký hiệu sech, cosec hyperbol - csch. Dưới đây là những công thức chi tiết để xác định:
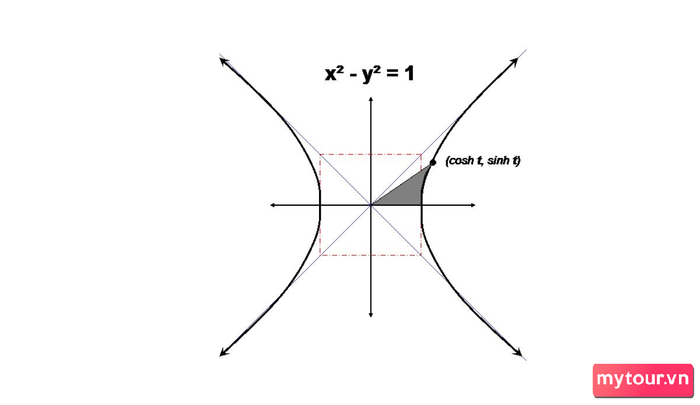
Nhìn nhận về những quy luật quan trọng của hàm Hyperbolic ngược:
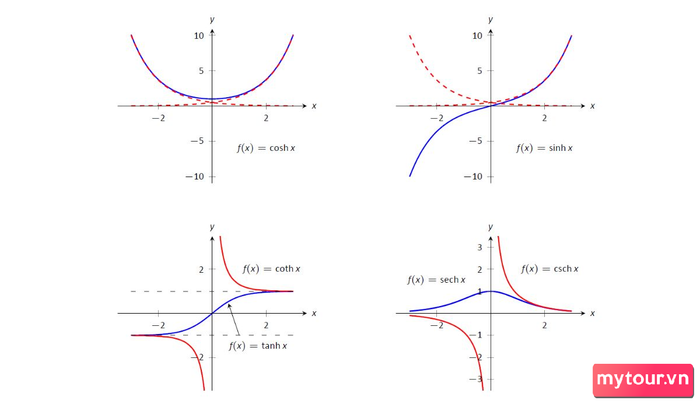
- Công thức hàm sinh: Sinh x = ex-e-x2- là hàm lẻ, đồ thị hàm số đối xứng qua trục hoành
- Công thức hàm cosh: Cosh x =ex+e-x2 - là hàm chẵn, đồ thị hàm số đối xứng qua trục tung
- Công thức hàm tanh: Tanh x = sinh xcosh x- là hàm lẻ, đồ thị hàm số đối xứng qua trục hoành.
- Công thức hàm coth: Coth x = cosh xsinh x- là hàm lẻ, đồ thị hàm số đối xứng qua trục hoành
- Công thức hàm sech: Sech x =1cosh x - là hàm chẵn, đồ thị hàm số đối xứng quan trung tung
- Công thức hàm csch: Csch x =1sinh x - là hàm lẻ, đồ thị hàm số đối xứng qua trục hoành.
Trong thế giới của các hàm số hyperbol, chúng vẫn giữ được tính chất linh hoạt khi thực hiện các phép tính như cộng, trừ và tính một nửa đối số.
Hàm Hyperbolic ngược
Hàm Hyperbolic ngược, được hình thành từ sự đảo ngược của hàm Hyperbolic. Còn được biết đến với tên gọi Hyperbolic nghịch đảo, và trong một số trường hợp, người ta thường gọi nó là “hàm diện tích” để nhận ra góc hyperbol.
Đối với mỗi điểm A (x1, y1) trên đồ thị Hyperbolic, góc tương ứng AOx luôn mang theo ý nghĩa của Hyperbolic ngược.
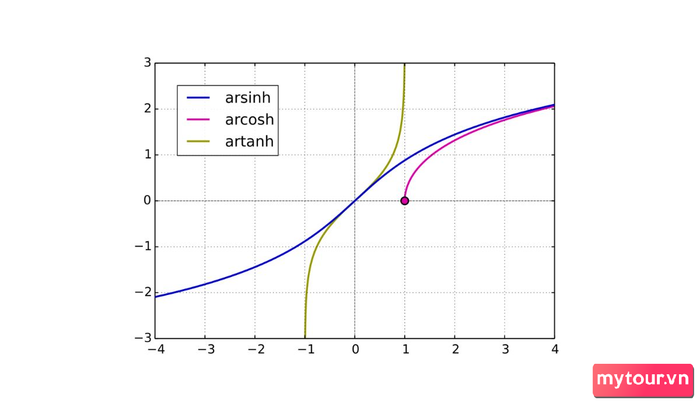
Nhìn nhận về những quy luật quan trọng của hàm Hyperbolic ngược:
- Công thức hàm sinh: Arsinh x = ln(x + x2+1 )
- Công thức hàm cosh: Arcosh x = ln(x + x2-1 )
- Công thức hàm tanh: Artanh x = 1/2 ln(1+x1-x)
- Công thức hàm coth: Arcoth x = 1/2 ln(x+1x-1)
- Công thức hàm sech: Arcech x = ln(1+1-x2x)
- Công thức hàm csch: Arcsch x = ln(1x+1x2+1)
Khi áp dụng các công thức có chứa x trong mẫu số, quan trọng phải đặt điều kiện xác định trước khi thực hiện các phép toán.
Hàm Hyperbolic cho số phức
Sự kết hợp mạnh mẽ giữa hàm Hyperbolic và hàm mũ được thể hiện rõ qua đồng nhất thức sau:
Biểu diễn hàm Hyperbol qua các đẳng thức: ex=cosh x + sinh x và e-x=cosh x - sinh x
Từ đó, mở rộng cách biểu diễn hàm Hyperbol dưới dạng số phức:

Ví dụ về hàm Hyperbolic
Hàm Hyperbol có đa dạng ứng dụng và cách tính. Để hiểu rõ hơn về những ứng dụng thực tế, tham khảo ví dụ về đẳng thức và tính tổng của dãy số sử dụng hàm Hyperbol.

Câu hỏi thường gặp về hàm Hyperbolic
Hàm Hyperbolic, một công cụ mạnh mẽ với nhiều ứng dụng. Khi sử dụng, có thể phát sinh những thắc mắc, hãy tham khảo những câu hỏi thường gặp dưới đây.
Tính đạo hàm của các hàm Hyperbolic
Đạo hàm của các hàm Hyperbolic chủ yếu dựa trên các công thức đạo hàm cơ bản như:
- (sinh x)’ = cosh x
- (cosh x)’ = sinh x
- (tanh x)’ = 1 -tanh2x=sech2x=acosh2x
- (coth x)’ = -coth x.csch x
- (sech x)’= -tanh x.sech x
Với việc sử dụng các công thức đạo hàm cơ bản, bạn có thể tận dụng chúng để tính toán các đạo hàm phức tạp hơn.
Phương pháp triển khai chuỗi Taylor cho hàm Hyperbolic
Chuỗi Taylor của một hàm số là tổng vô hạn các phần tử, được tạo ra khi bạn lấy đạo hàm của hàm số tại một điểm cụ thể. Tổng này có thể được biểu diễn một cách gọn nhẹ như sau:
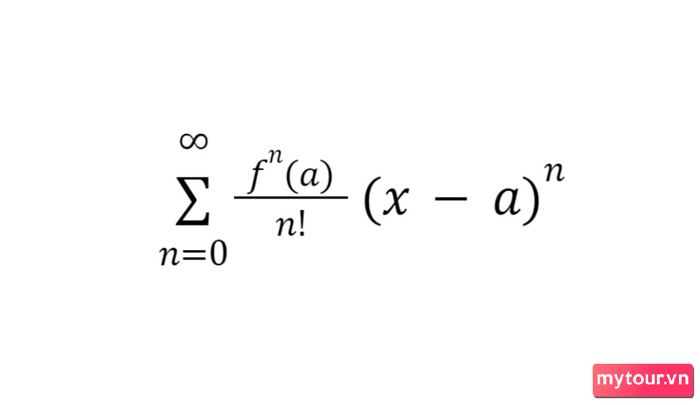
Ở đây, n là cấp độ của đạo hàm và a là điểm mà bạn chọn để tính đạo hàm.
Dựa trên nguyên lý này, có thể triển khai các công thức Hyperbolic theo chuỗi Taylor như sau:
- sinh x = x + x33!+ x55! + x77! +.....=n=0x2n+1(2n+1)!
- cosh x = x + x22!+ x44! + x66! +.....=n=0x2n(2n)!
- Tanh x = x - x33+ 2x515 - 17x7315 +.....=n=022n(22n-1)B2nx2n-1(2n+1)!, điều kiện |x| < 2
- Coth x = x-1+ x3- x345 + 2x5945 +.....=n=022n.B2nx2n-1(2n)!, điều kiện 0<|x|<
- Sech x = 1 - x23+ 5x424 - 61x6710 +.....=n=0E2nx2n(2n)!, điều kiện |x| < 2
Ở đây, B và E lần lượt là ký hiệu của số Bernoulli và Euler.
Đây là sự tập hợp của Mytour về lý thuyết của hàm Hyperbolic. Bạn có thể áp dụng những tính chất này không chỉ trong toán học mà còn ở các lĩnh vực khác.
