Khám Phá Hàm Ngược và Tính Độc Đáo của Đạo Hàm

Hàm Ngược không chỉ là khái niệm toán học khô khan, mà nó còn mang lại ứng dụng mạnh mẽ ngoài giảng đường. Người ta thậm chí áp dụng tính chất của Hàm Ngược để giải quyết những vấn đề không phải toán học. Vậy Hàm Số Ngược là gì mà lại quan trọng đến vậy? Hãy khám phá cùng Mytour để hiểu rõ hơn về khái niệm này và cách tính Đạo Hàm của Hàm Số Ngược.

Khám Phá Khái Niệm Hàm Ngược

Hàm Ngược, hay Hàm Nghịch Đảo, không chỉ là khái niệm trừu tượng mà còn là một công cụ mạnh mẽ trong giải quyết vấn đề. Cơ bản, Hàm Ngược là một hàm chứa biến là kết quả của một hàm khác.

Trong môn toán, Hàm Ngược đại diện cho việc hoàn tác lại những gì đã được tính toán trong một hàm. Nếu một hàm f có Hàm Nghịch Đảo tương ứng, ta nói hàm f là khả nghịch và ký hiệu Hàm Nghịch Đảo là f-1.

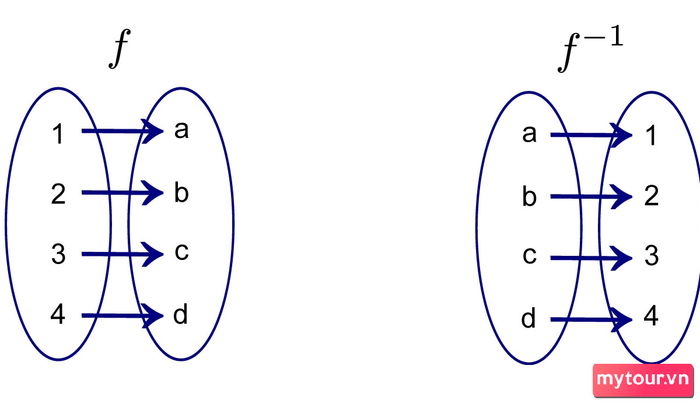Hàm Nghịch Đảo thường được biểu diễn với ký hiệu f-1

Điều Kiện Cần để Hàm Số f là Khả Nghịch

• f(x) = y
• f^-1(y)=x

Ở đây, f(x) là hàm có biến là x, trong khi f

^-1

(y) là hàm nghịch đảo của f(x) theo biến y.

Từ mối liên kết trên, hàm nghịch đảo của f(x) có dạng tổng quát như sau:

f

^-1

(y) = (phần tử duy nhất x ∊ X sao cho f(x) = y)

Công thức tính hàm nghịch đảo 

Với một số hàm cơ bản như ex, 2x,..., quá trình tìm hàm nghịch đảo có thể mất thời gian. Để giảm thiểu thời gian tính toán, bạn có thể tham khảo bảng dưới đây để tìm hàm nghịch đảo tương ứng. Để áp dụng công thức thành công, hãy lưu ý đến các điều kiện. Hàm không khả nghịch nếu không thỏa mãn điều kiện xác định.

Ví dụ về các hàm nghịch đảo cơ bản

Để giúp bạn hiểu sâu hơn về hàm nghịch đảo, Mytour sẽ mang đến một số ví dụ cụ thể như sau:

Hàm tuyến tính

Mỗi hàm tuyến tính luôn có một hàm nghịch đảo, có thể nói mọi hàm tuyến tính đều khả nghịch. Xét ví dụ với hàm f(x) = 2x - 3. Khi đó, hàm nghịch đảo của f(x) = 2x - 3 là f

^-1

(y) = (y + 3)/2.

Ví dụ về hàm ngược của hàm tuyến tính

Hàm mũ hai

Tất cả các hàm mũ hai đều không khả nghịch trên miền giá trị R. Để có khả nghịch, bạn cần xem xét hàm mũ hai trên khoảng giá trị không âm. Đối với hàm f(x) = x2 và miền giá trị là [0,), hàm ngược của nó f-1(y) = y.

Cách tính đạo hàm hàm nghịch

Trước khi tính đạo hàm của hàm nghịch đảo, cần xét tính khả vi của hàm. Nếu hàm f khả vi trên khoảng A, thì hàm nghịch đảo của hàm f, hay f-1, sẽ khả vi trên khoảng f(A). Theo định lý hàm ngược, đạo hàm của hàm này được tính theo công thức tổng quát:

(f

^-1

-1

Bảng công thức tính đạo hàm của hàm ngược f’(x)

Đặc tính của hàm ngược

Hàm nghịch đảo mang đến những đặc tính quan trọng dựa trên bản chất của hàm. Ứng dụng chúng để giải các vấn đề toán học là một cách hiệu quả.

Tính duy nhất

Mỗi hàm f duy nhất xác định một hàm nghịch đảo f

^-1

tương ứng. Ngược lại, mỗi hàm f chỉ có một hàm nghịch đảo duy nhất.

^-1

có nghĩa là mỗi hàm f đều tương ứng với một hàm nghịch đảo duy nhất.

Tính đối xứng

Hàm f và hàm nghịch đảo của nó thể hiện tính đối xứng trên đồ thị, đặc biệt qua trục Oxy.

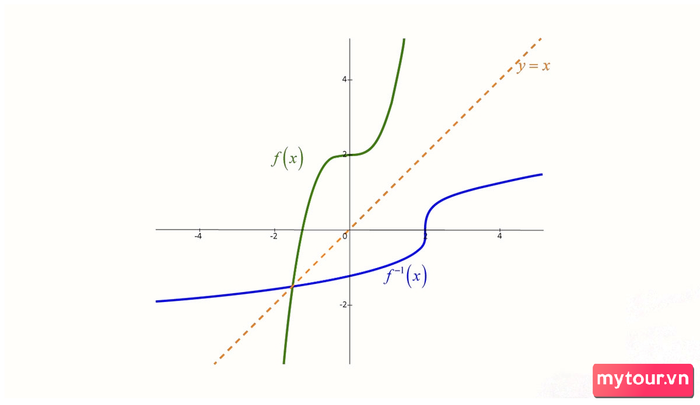Đồ thị đối xứng giữa hàm f(x) và hàm nghịch đảo f-1(x)

Qua đồ thị, tất cả các cặp hàm f và f

^-1

đều phản ánh đối xứng qua đường thẳng y=x. Không chỉ áp dụng cho hàm bậc 1 và bậc 2, tính chất này còn xuất hiện ở nhiều hàm sơ cấp khác.

Ngoài ra, tính đối xứng cũng thể hiện trong hàm hợp g°f, tuy nhiên, để thấy điều này, chúng ta cần sự hỗ trợ của tính toán đại số. Kết quả của hàm nghịch đảo của hàm hợp g°f được ký hiệu là (g°f)

^-1

= f

^-1

°g

^-1

. Trong quá trình tính toán hàm hợp, thứ tự của các hàm sẽ trải qua sự thay đổi đáng kể, đặc biệt là thứ tự của g sẽ đổi chỗ với f.

Đồ thị của hàm nghịch đảo

Dưới đây là đồ thị minh họa cho hàm nghịch đảo của hàm 2x:

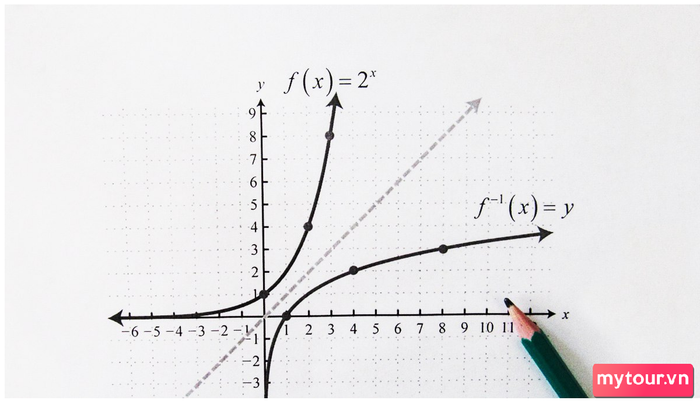Đồ thị của hàm f(x) = 2x và hàm ngược f-1(x) = lbx

Hàm tự nghịch đảo

Về bản chất, đây là một hàm đối xứng. Khi biểu diễn trên đồ thị, hàm tự nghịch đảo là trục đối xứng với chính nó và với các hàm khác. Hàm y = x được xem là một trong những hàm tự nghịch đảo đặc biệt đã được công bố.

Cách xử lý hàm ngược

Để tính toán hàm nghịch đảo, bạn cần tuân theo quy tắc và công thức áp dụng. Trong nội dung dưới đây, Mytour sẽ không chỉ cung cấp hai tài nguyên đó mà còn hướng dẫn cách tính đạo hàm của hàm nghịch đảo.

Bước vào thế giới của hàm ngược

• Bước 1: Đưa hàm đã cho về dạng y = f(x).
• Bước 2: Xét điều kiện song ánh của hàm f(x).
• Bước 3: Nếu thỏa điều kiện, thì chuyển đổi sang dạng x = f(y).
• Bước 4: Kết luận.

Phương pháp tìm hàm lượng giác nghịch đảo

Đối với hàm lượng giác nghịch đảo, áp dụng những bước cơ bản như đã mô tả trước đó. Cần chú ý rằng giá trị của hàm luôn nhỏ hơn 1 hoặc có dạng radian.

Giải bài tập thực hành về hàm ngược

Bài tập 1: Tìm hàm nghịch đảo của hàm f(x) = ln (x + 3)

Phân tích bài toán:

Điều kiện x (-3;∞)

Giả sử ln (x + 3) = y

Chuyển đổi: x + 3 = e

y

Kết quả: x = e

y - 3

Một cách khác để hiểu: x là số mà khi cộng thêm 3, sau đó lấy logarithm tự nhiên, sẽ thu được y.

Tổng hợp: x = e

^{Kết quả hàm nghịch đảo:}

-3

Hàm nghịch đảo của f(x) = ln (x + 3) là:

-1

= e^y - 3.

Bài tập 2: Tìm hàm nghịch đảo của f(x) = (3x + 2)/(x+1).

Kết quả hàm nghịch đảo:

Điều kiện: x ≠ -1

Hàm nghịch đảo của hàm f(x) = (3x + 2)/(x+1) là:

3x + 2 = y (x + 1)

3x + 2 = yx + y

3x - yx = y - 2

Kết quả hàm nghịch đảo:

⇔ x (3 - y) = y - 2

⇔ x = (y - 2)/(3-y)

^{Vậy hàm nghịch đảo của hàm f(x) là:}

(y - 2)/(3-y)

Một số bài tập tự luyện về hàm ngược:

Hàm ngược: Một Khám Phá Tinh Tế