1. Hình elip là gì?
- Theo Wikipedia: Hình elip là một đường cong phẳng bao quanh hai điểm cố định, sao cho tổng khoảng cách từ bất kỳ điểm nào trên đường cong đến hai điểm cố định này luôn không thay đổi. Hình tròn là trường hợp đặc biệt của hình elip khi hai điểm cố định trùng nhau. Độ dẹt của hình elip được thể hiện qua tâm sai e, biến thiên từ e = 0 (hình tròn) đến e = 1 (trường hợp parabol không còn là elip).
- Theo định nghĩa toán học:
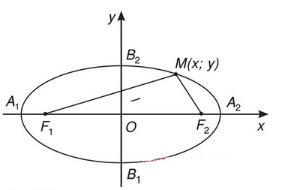
Xét hai điểm cố định F1 và F2 với khoảng cách F1F2 = 2c (với c > 0) và một hằng số a > c. Elip (E) là tập hợp các điểm M sao cho tổng khoảng cách từ M đến F1 và F2 luôn bằng 2a.
Các điểm F1 và F2 gọi là các tiêu điểm của elip (E).
Khoảng cách F1F2 = 2c được gọi là tiêu cự của elip (E).
Khoảng cách từ M đến các tiêu điểm F1 và F2 được gọi là bán kính qua tiêu.
2. Phương trình chuẩn của elip
- Điểm F1 có tọa độ (-c; 0), điểm F2 có tọa độ (x; 0)
M(x;y) thuộc (E) <=> x2 / a2 + y2 / b2 = 1 (1) với b2 = a2 - c2
Phương trình (1) được gọi là phương trình chuẩn của elip (E)
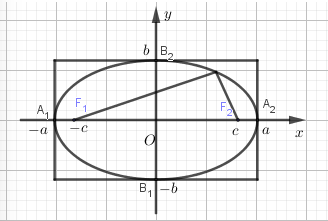
3. Đặc điểm và hình dáng của elip
Elip với phương trình (1) có các trục tọa độ là trục đối xứng và gốc tọa độ là tâm đối xứng
- Tiêu điểm: Tiêu điểm trái F1(-c; 0), tiêu điểm phải F2(x; 0)
- Các đỉnh: A1(-a; 0); A2(a; 0); B1(0; -b); B2(0; b)
- Trục lớn: A1.A2 = 2a, nằm trên trục Ox; trục nhỏ: B1.B2 = 2b, nằm trên trục Oy
- Hình chữ nhật được tạo bởi các đường thẳng x = ±a, y = ±b gọi là hình chữ nhật cơ sở.
- Tâm sai: e = c / a < 1
- Bán kính qua tiêu điểm của điểm M(xm; ym) thuộc elip (E) được tính như sau:
MF1 = a + exM = a + (c / a)xM, MF2 = a - exM = a - (c / a)xM
4. Độ lệch tâm của elip
- Độ lệch tâm của elip được xác định bằng tỷ lệ khoảng cách từ tâm của elip đến một trong hai tiêu điểm so với bán trục chính của elip.
- Độ lệch tâm của elip được tính bằng e = c / a
- Trong đó, c là khoảng cách từ tâm đến tiêu điểm và a là bán trục chính của elip
- Do c ≤ a nên độ lệch tâm luôn nhỏ hơn 1 đối với elip
5. Mối liên hệ giữa đường tròn và đường elip
- Theo công thức b2 = a2 - c2, nếu khoảng cách tiêu điểm của elip nhỏ hơn, thì b gần bằng a hơn, tức là trục nhỏ của elip gần bằng trục lớn. Khi đó, elip có hình dạng gần như một đường tròn.
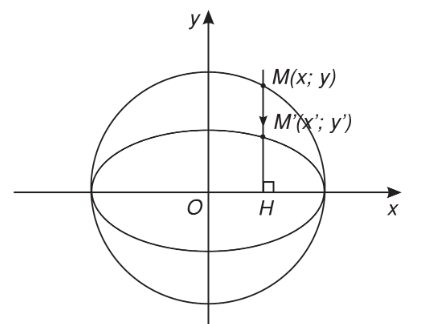
- Trong mặt phẳng Oxy, đường tròn (C) có phương trình: x2 + y2 = a2
Đối với mỗi điểm M(x; y) trên đường tròn, ta xét điểm M'(x'; y') sao cho:
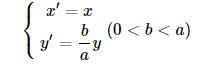
Tập hợp các điểm M' thỏa mãn phương trình x2 / a2 + y2 / b2 = 1 là một elip (E)
Lúc này, ta nói rằng đường tròn (C) đã được biến dạng thành elip (E)
6. Diện tích của hình elip
Hình elip có hai trục đối xứng A1A2 và B1B2 vuông góc với nhau, giao nhau tại tâm O. Các trục này cắt elip tại các điểm A1A2 (trục lớn) và B1B2 (trục nhỏ). Nửa chiều dài của trục lớn là (a), còn trục nhỏ là (b). Từ tâm elip O đến các tiêu điểm F1 và F2 gọi là bán tiêu cự (c).
Do đó, A1, A2, B1, B2 là các đỉnh của elip; B1B2 là trục nhỏ (2b); A1A2 là trục lớn (2a); F1F2 là khoảng cách giữa các tiêu điểm (2c).
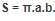
Vì vậy, khi biết chiều dài của trục lớn và trục nhỏ, bạn có thể dễ dàng tính diện tích của elip.
7. Các bài tập thực hành về hình elip
Bài 1. Cho elip (E) với phương trình x2 / 16 + y2 / 12 = 1 và điểm M nằm trên elip. Nếu hoành độ của điểm M là 1, hãy tính khoảng cách từ M đến hai tiêu điểm của elip.
Giải pháp:
Ta có: a2 = 16, b2 = 12
Do đó, c2 = a2 - b2 = 4
→ a = 4; c = 2 và hai tiêu điểm là F1(-2;0) và F2(2;0)
M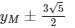
Độ lệch tâm của elip được tính bằng e = c / a → e = 2 / 4 = 0.5
→ Khoảng cách từ M đến tiêu điểm F1 là MF1 = a + e xM = 4 + 0.5 = 4.5
Khoảng cách từ M đến tiêu điểm F2 là MF2 = a - e xM = 4 - 0.5 =
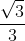
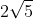
Giải pháp:
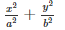
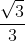
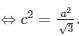
Chiều dài đường chéo của hình chữ nhật:
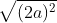 2222
2222Do đó: a2 = b2 + c2 <=> a2 = 5 - a2 + a2 / 3 <=> a2 = 3 => b2 = 2
Vì vậy, phương trình chuẩn của elip (E) là x2 / 3 + y2 / 2 = 1
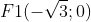
Giải pháp:
Đặt phương trình chuẩn của elip (E) dưới dạng: x2 / a2 + y2 / b2 với điều kiện a > b > 0
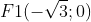
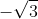 22222
22222Điểm M(x0;y0)
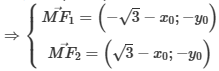
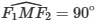
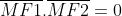
<=> X02 - 3 + y02 = 0
<=> x02 + y02 = 3
F1MF212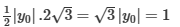
<=> y02 = 1/3
<=> x02 = 8/3
Ngoài ra, điểm M(x0;y0) nằm trên E
<=> x02/a2 + y02/b2 = 1
<=> 8/3a2 + 1/3b2 = 1 (2)
Thay (1) vào (2) ta có:
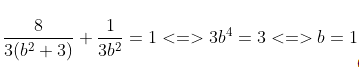
<=> a2 = 4
Vậy phương trình chuẩn của elip (E) cần viết là: x2/4 + y2 = 1
Bài 4. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 = 8. Biết rằng (E) có trục chính dài bằng 8 và (E) cắt (C) tại bốn điểm tạo thành các đỉnh của một hình vuông. Tìm phương trình chuẩn của elip (E)
Giải:
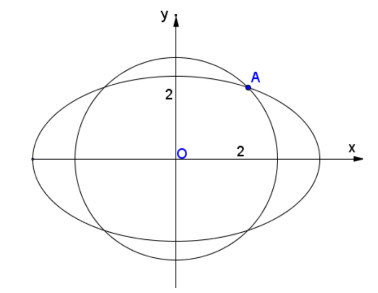
Phương trình chuẩn của elip (E) có dạng: x2/a2 + y2/b2 = 1
- Vì (E) có trục chính dài 8 nên 2a = 8, suy ra a = 4
- (E) cắt (C) tại 4 điểm phân biệt, tạo thành các đỉnh của một hình vuông, nghĩa là 4 đỉnh nằm trên hai đường phân giác của góc phần tư thứ nhất và thứ hai.
Giả sử A là một điểm giao của (E) và (C) nằm trên đường phân giác delta: y = x
- Gọi A(t;t) thuộc denta (t > 0). Ta có: A thuộc (C) => t² + t² = 8 => t = 2
(vì t > 0) => A (2;2)
- Mà A thuộc (E) => 2² / 4² + 2² / b² = 1 => b² = 16 / 3
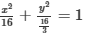
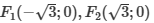
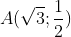 222
222Giải thích:
- Phương trình chuẩn của elip (E) có dạng: x² / a² + y² / b² = 1 với a > b > 0
.png)
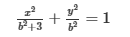
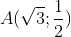
.png)
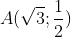
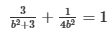
<=> ab2 - b2 - 3 = 0 <=> (4b2 +3)(b2 - 1) = 0
<=> b2 = 1 => a2 = 4
Vậy phương trình chuẩn của (E) là: x2 / 4 + y2 = 1
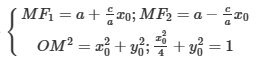
Khi đó:
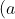
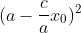 020
020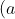
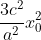 0202
0202= 4 + 9 / 4 . x02 - 3(x02 + y02)
= 4 - 3(x02 / 4 + y02)
= 4 - 3 = 1
Do đó P = 1
Bài 6. Cho elip (E) có tiêu cự 2c, trục lớn và trục nhỏ lần lượt là 2a và 2b. Trong các mệnh đề dưới đây, mệnh đề nào là đúng?
A. c < b < a
B. c < a < b
C. c > b > a
D. c < a và b < a
Đáp án là:
Cách giải:
Áp dụng lý thuyết về phương trình chuẩn của elip
Phương trình chuẩn của elip có dạng x2 / a2 + y2 / b2 = 1 với a > b và a2 = b2 + c2, trong đó 2c là tiêu cự của elip.
Chi tiết giải:
Vì a2 = b2 + c2 và a, b, c > 0 nên a2 > c2, suy ra a > c. Rõ ràng b < a
Chọn đáp án D.
