Khám phá định nghĩa về giải thuật và cách xây dựng giải thuật một cách đơn giản, dễ hiểu

Tìm hiểu về khái niệm giải thuật, những nguyên tắc cơ bản cho người mới bắt đầu trong thế giới lập trình. Điều gì làm nên một giải thuật đơn giản? Hãy theo dõi bài viết dưới đây!

Khám phá khái niệm về giải thuật

I. Định nghĩa về giải thuật

1. Khái niệm cơ bản

Giải thuật (hoặc thuật toán) là một bộ hướng dẫn giới hạn để thực hiện theo một trình tự nhất định để đạt được kết quả mong muốn. 

Giải thuật là bộ hướng dẫn thao tác để giải quyết vấn đề một cách ngắn gọn.

Khám phá giải thuật qua việc áp dụng tập hợp các thao tác để giải quyết vấn đề cụ thể.

Ví dụ đơn giản về việc áp dụng giải thuật để nấu cơm và những bước cụ thể trong quá trình đó.

• Lấy gạo - vo gạo - đong nước - đặt vào nồi - đậy nắp - cắm điện - bật nút - đợi cơm chín.

Giải thuật không phụ thuộc vào ngôn ngữ lập trình, có thể triển khai trong nhiều ngôn ngữ khác nhau.

2. Đặc trưng của giải thuật được thể hiện qua tính độc lập với ngôn ngữ lập trình.

Không phải mọi thủ tục đều là giải thuật. Một giải thuật cần có những đặc điểm sau:

• Tính xác định: Mỗi giai đoạn hay bước của giải thuật phải rõ ràng và mục đích duy nhất.
• Dữ liệu đầu vào xác định: Có hoặc không dữ liệu đầu vào, nhưng nếu có, phải xác định.
• Kết quả đầu ra: Có một hoặc nhiều dữ liệu đầu ra xác định, phù hợp với kiểu kết quả mong muốn.
• Tính dừng: Phải kết thúc sau một số bước hữu hạn.

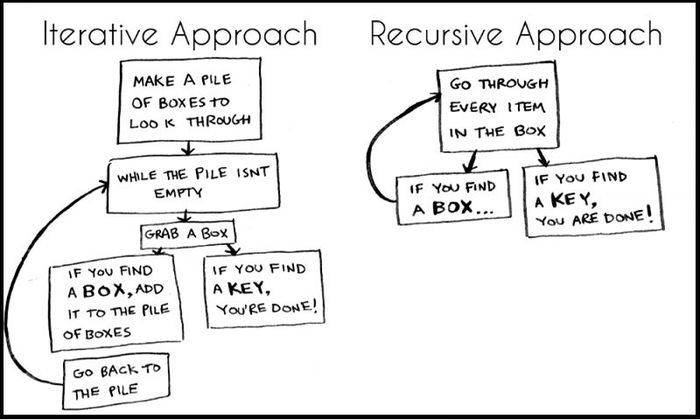
Giải thuật dừng lại sau một số bước nhất định.

• Tính hiệu quả: Có thể thi hành hiệu quả với nguồn tài nguyên có sẵn.
• Tính phổ biến: Có thể giải quyết một loạt vấn đề tương tự.
• Độc lập: Chỉ thị không phụ thuộc vào ngôn ngữ lập trình cụ thể.

3. Tầm quan trọng của giải thuật trong lập trình.

Cấu trúc dữ liệu và giải thuật đóng vai trò quan trọng trong lập trình, không chỉ với ngôn ngữ Java, PHP, Python mà còn với mọi ngôn ngữ lập trình khác.

Chuyển đổi ngôn ngữ lập trình không phức tạp. Cấu trúc dữ liệu và giải thuật là yếu tố quyết định. Tư duy giải thuật giúp hoàn thành nhiệm vụ lập trình.

II. Cách thiết kế giải thuật

1. Ngôn ngữ viết 

Thiết kế giải thuật bằng ngôn ngữ tự nhiên, liệt kê tuần tự bước xử lý thuật toán. 

Ưu điểm: 

Đơn giản, không yêu cầu kiến thức về biểu diễn (mã giả, lưu đồ,...)

Nhược điểm:

• Dài dòng, thiếu cấu trúc.
• Có khi khó hiểu và không biểu diễn thuật toán hiệu quả.

Ví dụ: Sử dụng ngôn ngữ viết để tìm 3 số lớn nhất trong a, b, c

• Bước 1: Gán max = a.
• Bước 2: Nếu b > max thì gán max = b.
• Bước 3: Nếu c > max thì max chính là c.

2. Lưu đồ

Lưu đồ bao gồm: 

• Điểm khởi đầu và điểm kết thúc.
• Thao tác nhập/xuất dữ liệu.
• Thao tác xử lý.
• Quyết định rẽ nhánh.
• Luồng tiến trình.
• Ghi chú.
• Ký hiệu kết nối giữa các trang hoặc sang trang khác. 

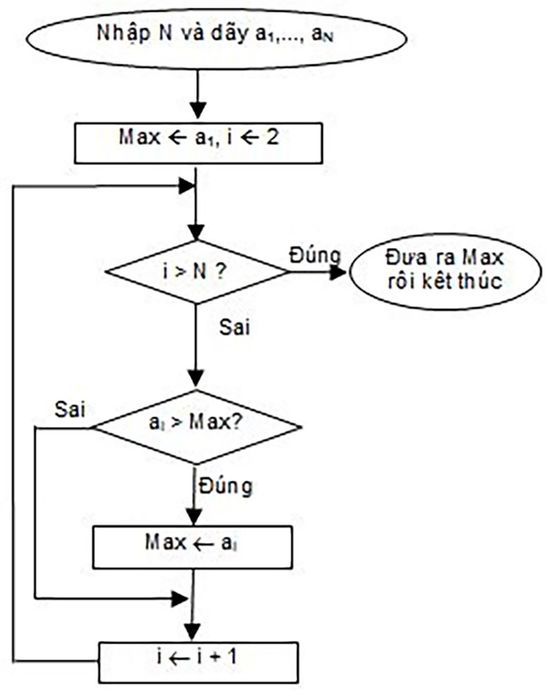
Lưu đồ

Ưu điểm: 

Trực quan, dễ hình dung. 

Nhược điểm: 

Cồng kềnh khi đối mặt với vấn đề xử lý quá phức tạp. 

3. Mã giả

Mã giả là ngôn ngữ khá tương đồng với ngôn ngữ lập trình. Thường sử dụng cấu trúc chuẩn hóa, giống như ngôn ngữ Pascal, C. Có sử dụng các ký hiệu toán học, biến và hàm.

Một ví dụ về mã giả

Ưu điểm: 

Không phức tạp như lưu đồ khối

Nhược điểm:

Không thể hiện một cách rõ ràng như lưu đồ khối.

4. Lập trình

• Sử dụng ngôn ngữ máy tính (C, Pascal,...) để biểu diễn thuật toán, cấu trúc dữ liệu thành câu lệnh.
• Áp dụng phương pháp từng bước để chuyển đổi bài toán thành mã chương trình cụ thể.
• Phát triển kỹ năng lập trình yêu cầu học tập và thực hành đều đặn.

Viết chương trình "Hello World" bằng ngôn ngữ Java

III. Đánh giá giải thuật (Mô tả + hình ảnh)

1. Tại sao cần phân tích giải thuật

Trong quá trình giải quyết một vấn đề, chúng ta thường đối mặt với nhiều giải thuật khác nhau. Quan trọng là phải đánh giá và chọn lựa giải thuật phù hợp nhất.

2. Phân tích lý thuyết

Đây là phân tích dựa trên lý thuyết, đánh giá hiệu suất của giải thuật giả định rằng các yếu tố khác (như tốc độ xử lý, ...) là hằng số và không ảnh hưởng đến triển khai thực tế.

3. Phân tích tiệm cận:

Phân tích này thường được thực hiện sau khi giải thuật được triển khai trên một ngôn ngữ lập trình cụ thể.

Sau khi chạy và đánh giá các tham số liên quan, hiệu suất của giải thuật được đo lường bằng các thông số như thời gian thực hiện, lượng bộ nhớ sử dụng, ...

IV. Độ phức tạp của giải thuật

1. Khái niệm về Độ phức tạp của giải thuật

Độ phức tạp giải thuật là một ước lượng (có thể không chính xác) về số phép tính mà giải thuật cần thực hiện (dựa trên đó để suy ra thời gian thực hiện của giải thuật) đối với bộ dữ liệu đầu vào (Input) có kích thước n.

Trong ngữ cảnh cụ thể, n có thể là số phần tử của mảng trong bài toán sắp xếp hoặc tìm kiếm, hoặc đơn giản là độ lớn của số trong bài toán kiểm tra số nguyên tố, …

Cho rằng X là một giải thuật và n là kích thước của dữ liệu đầu vào. Thời gian và lượng bộ nhớ sử dụng bởi giải thuật X đều là yếu tố quyết định hiệu quả của X:

• Thời gian: Được đánh giá dựa trên số phép tính chính (như phép so sánh trong thuật toán sắp xếp).

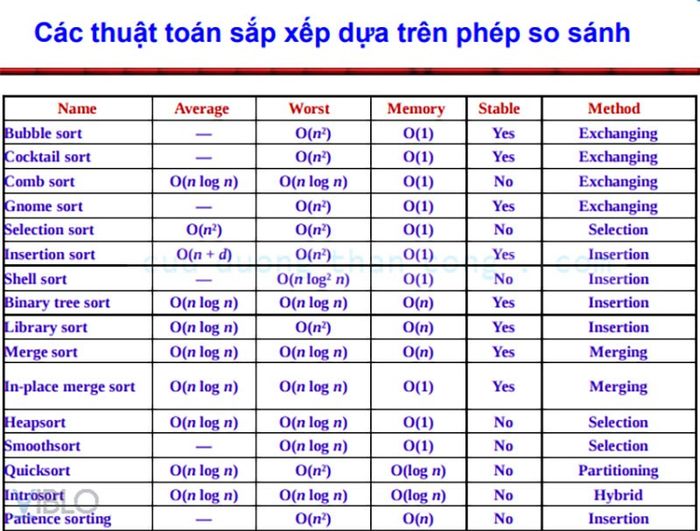
Các so sánh trong thuật toán sắp xếp

• Yếu tố bộ nhớ: Lượng bộ nhớ được ước lượng thông qua việc đo lường bộ nhớ tối đa mà giải thuật cần sử dụng.

Độ phức tạp của một giải thuật (được biểu diễn bằng hàm f(n)) mang lại mối liên quan giữa thời gian thực hiện và/hoặc lượng bộ nhớ cần thiết cho giải thuật.

2. Độ phức tạp bộ nhớ trong phân tích giải thuật (Khả năng sử dụng bộ nhớ)

Yếu tố bộ nhớ của giải thuật đại diện cho lượng bộ nhớ mà giải thuật yêu cầu trong quá trình thực hiện. 

Lượng bộ nhớ (giả sử là S(P)) mà giải thuật sử dụng bao gồm tổng của hai thành phần sau:

• Phần hằng số (hay còn được gọi là C) đại diện cho lượng bộ nhớ cần thiết để lưu trữ dữ liệu và các biến tĩnh, hoàn toàn không phụ thuộc vào kích thước của vấn đề. Ví dụ: các biến và các hằng số cơ bản, …
• Phần biến động (có tên gọi là SP(I)) là lượng bộ nhớ yêu cầu bởi các biến, có kích thước phụ thuộc vào kích thước của vấn đề. Ví dụ: cấp phát bộ nhớ động, cấp phát bộ nhớ đệ quy, …

Dựa trên đó, chúng ta có công thức S(P) = C + SP(I). Hãy xem xét ví dụ đơn giản sau:

Trong trường hợp này, chúng ta sử dụng ba biến A, B và C cùng một hằng số. Vì thế: S(P) = 1+3.

Giờ đây, lượng bộ nhớ sẽ phụ thuộc vào loại dữ liệu của các biến và hằng đã được đề cập và sẽ là tích của tổng trên với bộ nhớ cho loại dữ liệu tương ứng.

3. Độ phức tạp thời gian trong phân tích giải thuật (Độ phức tạp thời gian)

Nhân tử thời gian của một giải thuật mô tả lượng thời gian chạy cần thiết từ khi bắt đầu đến khi kết thúc một giải thuật cụ thể. 

Thời gian yêu cầu có thể được biểu diễn qua một hàm T(n), trong đó T(n) có thể được đo lường như là số bước thực hiện.

Ví dụ, phép cộng hai số nguyên n-bit sẽ mất n bước. Do đó, tổng thời gian tính toán có thể được biểu diễn bởi T(n) = c*n

Ở đây, chúng ta quan sát hàm T(n) tăng tuyến tính khi kích cỡ dữ liệu đầu vào tăng.

Dưới đây là khái niệm về giải thuật và cách thiết kế giải thuật một cách đơn giản, dễ hiểu. Mong rằng bài viết này sẽ mang lại giá trị cho bạn. Đừng ngần ngại chia sẻ nếu bạn cảm thấy hữu ích nhé!