Khám phá lý thuyết và công thức cấp số nhân cùng bài tập có lời giải chi tiết

Công thức cấp số nhân là một kiến thức quan trọng trong chương trình Toán học lớp 12 mà học sinh cần nắm vững. Trong bài viết này, Mytour sẽ cung cấp cho bạn cái nhìn tổng quan về khái niệm, tính chất, và các công thức tính cấp số nhân. Bên cạnh đó, bài viết sẽ hướng dẫn bạn cách giải 5 dạng bài tập phổ biến và áp dụng chúng hiệu quả trong học tập và ôn thi.

Lý thuyết về cấp số nhân

Cấp số nhân (Geometric Sequence) là một dãy số đặc biệt, trong đó mỗi số hạng sau được tính bằng cách nhân số hạng trước đó với một hằng số cố định. Để hiểu rõ hơn về công thức tính cấp số nhân và các đặc điểm của dãy số này, hãy cùng tìm hiểu các khái niệm cơ bản dưới đây:

Cấp số nhân là gì?

Một dãy số được gọi là cấp số nhân khi mỗi số hạng từ số hạng thứ hai trở đi được tính bằng cách nhân số hạng trước đó với một hằng số cố định. Hằng số này, gọi là công bội, ký hiệu là q, đóng vai trò quan trọng trong công thức cấp số nhân, giúp ta tính toán các số hạng tiếp theo trong dãy.

Ví dụ: Xét dãy số 3, 6, 12, 24, 48,... là một cấp số nhân với:

• Số hạng đầu tiên: u₁ = 3
• Công bội q = 2 (vì 6/3 = 12/6 = 24/12 = 48/24 = 2)
• Số hạng tiếp theo có thể được tính bằng cách nhân số hạng hiện tại với 2 (q = 2)

Để việc tính toán cấp số nhân trở nên thuận tiện hơn, bạn nên sử dụng một chiếc laptop để thao tác nhanh chóng với các công thức và dãy số phức tạp. Laptop giúp bạn tiết kiệm thời gian, kiểm tra kết quả dễ dàng và lưu trữ bài tập một cách có hệ thống. Hiện nay, học sinh và sinh viên có nhiều lựa chọn laptop với giá cả hợp lý, ví dụ như:

Cấp số nhân lùi vô hạn là gì?

Cấp số nhân lùi vô hạn là một dãy số mở rộng về phía âm vô hạn, nghĩa là các chỉ số n của các số hạng sẽ nhỏ hơn 0. Đây là một khái niệm quan trọng trong việc mở rộng lý thuyết cấp số nhân, và công thức tính cấp số nhân lùi vô hạn được xác định bằng cách chia mỗi số hạng cho công bội q, thay vì nhân như trong cấp số nhân thông thường.

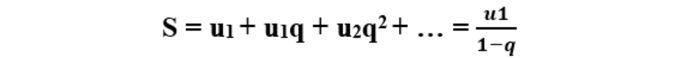
Ví dụ: Cho cấp số nhân có u₁ = 16 và công bội q = 2, khi lùi vô hạn ta có dãy số: ... 2, 4, 8, 16, 32, 64,... với điều kiện:

• u₁ = 16 (số hạng đầu tiên của dãy)
• u₀ = 8 (kết quả từ 16 chia cho 2)
• u₋₁ = 4 (kết quả từ 8 chia cho 2)
• u₋₂ = 2 (kết quả từ 4 chia cho 2)

Những tính chất cơ bản của cấp số nhân

Để có thể giải quyết các bài toán về cấp số nhân, điều quan trọng là nắm vững những đặc điểm cơ bản của nó. Một trong những tính chất quan trọng nhất là tỷ số giữa hai số hạng liên tiếp luôn không thay đổi, và bằng công bội q, được thể hiện qua công thức un+1/un = q, với mọi số tự nhiên n. Dựa vào tính chất này, ta có thể tìm công thức chung để tính số hạng thứ n: un = u1 × q^(n-1), với u1 là số hạng đầu tiên trong dãy.

Một đặc tính khác rất đặc biệt của cấp số nhân là khi ta lấy tích của hai số hạng cách đều một số hạng bất kỳ, kết quả sẽ luôn bằng bình phương của số hạng ở giữa. Cụ thể, nếu xét ba số hạng liên tiếp uk, uk+1, uk+2 thì ta có công thức: uk × uk+2 = (uk+1)². Hơn nữa, khi tất cả các giá trị trong dãy đều là số dương, trung bình nhân của hai số hạng bất kỳ sẽ bằng số hạng nằm giữa chúng, nếu như số hạng ở giữa là lẻ.

Công thức cấp số nhân

Sau khi đã hiểu rõ về định nghĩa và các tính chất của cấp số nhân, bước tiếp theo là tìm hiểu về các công thức tính cấp số nhân. Những công thức này sẽ giúp bạn tính toán và xác định các số hạng trong dãy một cách chính xác, từ đó áp dụng vào các bài toán thực tế một cách hiệu quả. Dưới đây là các công thức bạn cần nắm vững:

Công thức truy hồi

Công thức: un = un-1 . q với n∈N∗

Công thức truy hồi là một trong những công thức cơ bản và quan trọng của cấp số nhân, giúp mô tả mối liên kết giữa các số hạng liên tiếp trong dãy. Theo quy tắc này, để tính số hạng thứ n (ký hiệu là un), bạn chỉ cần lấy số hạng trước đó (un-1) nhân với công bội q. Ví dụ, với dãy số cấp số nhân 2, 6, 18, 54,... và công bội q = 3, ta có u3 = u2 × 3 = 6 × 3 = 18, và tiếp theo u4 = u3 × 3 = 18 × 3 = 54.

Công thức cấp số nhân

Công thức: un = u1 . q(n-1)

Đây là công thức tổng quát dùng để tính trực tiếp số hạng thứ n trong cấp số nhân mà không cần tính từng số hạng trung gian. Để tìm số hạng thứ n (un), bạn chỉ cần biết số hạng đầu tiên (u1) và công bội q, sau đó nhân u1 với q nâng lên lũy thừa (n-1). Ví dụ, với dãy số 2, 6, 18, 54,... và u1 = 2, q = 3, ta có thể tính trực tiếp u4 = 2 × 3(4-1) = 2 × 3³ = 2 × 27 = 54 mà không cần tính u2 và u3.

How to calculate the common ratio q of a geometric sequence

Formula: q = (un+1)/un

This formula helps determine the value of the common ratio by comparing the ratio between consecutive terms. Specifically, q can be calculated by dividing any term by its preceding term. For example, in the sequence 3, 9, 27, 81,..., we can calculate q = 9/3 = 3, or q = 27/9 = 3, or q = 81/27 = 3. This illustrates the constant nature of the common ratio in a geometric sequence.

Formula for calculating the sum of the first n terms

Formula: Sn = u1(1-qn)/(1-q)

Instead of adding each term individually, we can use the formula to calculate the sum of the first n terms of a geometric sequence. The three necessary elements for applying this formula are: the first term (u1), the common ratio (q), and the number of terms to sum (n). For example, in the sequence 2, 6, 18, 54,... (u1 = 2, q = 3), to find the sum of the first 4 terms, we use S4 = 2(1-3⁴)/(1-3) = 2(1-81)/-2 = 2×80/2 = 80, eliminating the need to manually add 2 + 6 + 18 + 54.

Formula for calculating the sum of an infinite geometric sequence

Formula: S = u1/(1−q)

This infinite geometric series formula is used to calculate the sum of a sequence with an infinite number of terms, provided that |q| < 1 to ensure the series converges. This is a special method for calculating the sum of infinite sequences. For example, in the sequence 1 + 1/2 + 1/4 + 1/8 + ... with u1 = 1 and q = 1/2, applying the rule gives S = 1/(1-1/2) = 1/(1/2) = 2, which provides the exact result for the infinite sum.

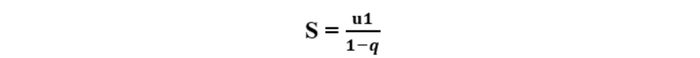
Summary of problem types applying the geometric sequence formula

Frequent practice with different problem types involving the geometric sequence formula is an effective way to master and apply this knowledge in real life. By solving a variety of problems, students will gain a deeper understanding of the formula and properties of geometric sequences, as well as enhance their logical thinking and problem-solving skills. Some of the typical problem types students often encounter include:

Type 1: Identifying a Geometric Sequence

Calculation method: q = un+1 / un (n = 1, n>1)

Conclusion:

• Case 1: If q changes, then un is not a geometric sequence.
• Case 2: If q remains constant, then un is a geometric sequence.

Example: Consider the sequence (2, 6, 18, 54). Determine if this sequence is a geometric sequence.

Solution:

1. Apply the geometric sequence formula to calculate the ratios q:
   • q₁ = u₂/u₁ = 6/2 = 3
   • q₂ = u₃/u₂ = 18/6 = 3
   • q₃ = u₄/u₃ = 54/18 = 3
2. Observation: Since the ratios q₁ = q₂ = q₃ = 3 are all equal, the sequence (2, 6, 18, 54) is a geometric sequence with common ratio q = 3 and u₁ = 2.

Type 2: Finding the common ratio of a geometric sequence

Solution method:

• Case 1: Use the formula q = un+1/un when two consecutive terms are given.
• Case 2: Use the formula un = u1 × q(n-1) when the first term and any term in the sequence are known.
• Case 3: Use the property of the product of two equally spaced terms when three terms are known.

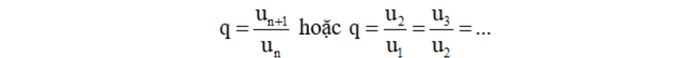
Example: A geometric sequence is given with the first term u₁ = 2, and the fourth term u₄ = 54. Find the common ratio q of the sequence.

Solution:

1. Áp dụng công thức cấp số nhân cho trường hợp thứ hai, ta có:
   • u₄ = u₁ × q³ (vì n = 4)
   • 54 = 2 × q³
2. Giải phương trình:
   • q³ = 54/2 = 27
   • q = ∛27 = 3
3. Kết luận: Công bội của cấp số nhân là q = 3 (Kiểm tra: với q = 3, dãy số là: 2, 6, 18, 54,...)

Dạng 3: Tìm số hạng trong cấp số nhân

Phương pháp tìm: 

• Trường hợp 1: Áp dụng công thức un = u1.q(n-1) khi đã biết số hạng đầu và công bội.
• Trường hợp 2: Áp dụng công thức un = un-1.q khi đã có số hạng trước và công bội.
• Trường hợp 3: Sử dụng tính chất của hai số hạng cách đều khi đã biết số hạng ở giữa.

Ví dụ: Một khách hàng gửi tiền tiết kiệm với số vốn ban đầu là 10 triệu đồng và lãi suất 8% mỗi năm. Hỏi tổng số tiền khách hàng này sẽ nhận được sau 3 năm (giả sử tiền lãi được cộng gốc hàng năm)?

Cách giải:

1. Áp dụng công thức cấp số nhân với các thông số như sau:
   • u₁ = 10 triệu đồng (số tiền ban đầu)
   • q = 1.08 (hệ số tăng mỗi năm, tương đương với 100% + 8% = 108% = 1.08)
   • n = 3 (số năm)
2. Áp dụng công thức tổng quát, ta có:
   • u₃ = u₁ × q²
   • u₃ = 10 × (1.08)²
   • u₃ = 10 × 1.1664
   • u₃ = 11.664 triệu đồng

Vậy số tiền khách hàng sẽ nhận được sau 3 năm là 11.664 triệu đồng, tương đương 11.664.000 đồng.

Dạng 4: Tính tổng cấp số nhân của n số hạng đầu tiên trong dãy

Phương pháp tính tổng n số hạng trong dãy cấp số nhân:

• Trường hợp 1: Áp dụng công thức Sn = u₁(1-qⁿ)/(1-q) khi q ≠ 1.
• Trường hợp 2: Sử dụng công thức Sn = nu₁ khi q = 1.
• Trường hợp 3: Nếu n nhỏ, có thể tính từng số hạng rồi cộng lại.

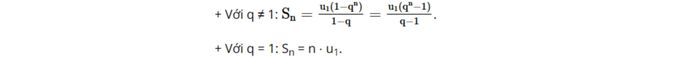
Công thức cấp số nhân giúp tính nhanh tổng n phần tử đầu tiên

Ví dụ: Cho cấp số nhân với u₁ = 3, q = 2. Hãy tính tổng của 5 số hạng đầu tiên trong dãy này.

Cách giải:

1. Các giá trị đã cho như sau:
   • u₁ = 3
   • q = 2
   • n = 5
2. Áp dụng công thức tính tổng, ta có:
   • S₅ = u₁(1-q⁵)/(1-q)
   • S₅ = 3(1-2⁵)/(1-2)
   • S₅ = 3(1-32)/(-1)
   • S₅ = 3 × 31
   • S₅ = 93

Kiểm tra: Dãy số 3, 6, 12, 24, 48; Tổng = 3 + 6 + 12 + 24 + 48 = 93.

Kết quả, tổng của 5 số hạng đầu tiên trong dãy cấp số nhân là 93.

Dạng 5: Tìm cấp số nhân

Phương pháp tìm cấp số nhân:

• Trường hợp 1: Áp dụng công thức cấp số nhân để tính u1 và q từ hai số hạng đã cho.
• Trường hợp 2: Sử dụng hệ phương trình dựa trên các điều kiện của bài toán để tìm u1 và q.
• Trường hợp 3: Dùng tổng Sn và một số hạng trong dãy để thiết lập phương trình và giải.

Ví dụ: Tìm cấp số nhân khi biết tổng ba số hạng đầu tiên là 26 và tổng hai số hạng cuối là 20.

Cách giải:

1. Giả sử ta có dãy cấp số nhân với ba số hạng lần lượt là u₁, u₂, u₃
   • S₃ = u₁ + u₂ + u₃ = 26 (1)
   • u₂ + u₃ = 20 (2)
   • u₂ = u₁.q và u₃ = u₁.q²
2. Thay các biểu thức vào (1) và (2):
   • u₁ + u₁q + u₁q² = 26
   • u₁q + u₁q² = 20
   • u₁(1 + q + q²) = 26 (3)
   • u₁(q + q²) = 20 (4)
3. Từ (3) và (4):
   • u₁ = 6 và q = 2
4. Vậy, dãy cấp số nhân ta tính được là: 6, 12, 24

Lưu ý: Các công thức cấp số nhân trên là chuẩn mực trong toán học, bạn có thể áp dụng chúng vào mọi bài toán về dãy số có công bội không đổi để có kết quả chính xác.

Trên đây là tổng hợp toàn bộ kiến thức về công thức cấp số nhân mà Mytour đã chia sẻ với các bạn học sinh. Với việc hiểu rõ khái niệm, tính chất và các công thức quan trọng, các bạn có thể tự tin giải quyết 5 dạng bài tập thường gặp về cấp số nhân. Hy vọng bài viết này sẽ giúp các bạn tích lũy thêm kiến thức và có phương pháp học tập hiệu quả để đạt kết quả cao trong kỳ thi sắp tới.