Khám phá mối quan hệ giữa x1 và x2 không phụ thuộc vào m

Buzz

Nội dung bài viết

1. Phương pháp giải quyết

2. Ví dụ

3. Bài tập thực hành

4. Bài tập tự luyện

Xem thêm

Trong các bài thi toán học, một dạng bài tập phổ biến là xác định mối liên hệ giữa x1 và x2 mà không bị ảnh hưởng bởi m. Hãy cùng Mytour tìm hiểu chi tiết qua bài viết sau đây.

1. Phương pháp giải quyết

Để xác định mối quan hệ giữa các nghiệm x₁ và x₂ của phương trình bậc hai mà không phụ thuộc vào tham số, bạn có thể thực hiện theo các bước sau:

₁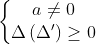 $\left\{\begin{matrix} a \neq 0 & \\ \Delta \left( \Delta ' \right) \geq 0 & \end{matrix}\right.$ $\left\{\begin{matrix} x_{1} + x_{2} = \frac{-b}{a} = f\left(m\right) & \\ x_{1} x_{2} = \frac{c}{a} = g\left(m\right) & \end{matrix}\right.$

Bước 3: Loại bỏ m khỏi hệ phương trình trên để xác định mối liên hệ giữa x₁ và x₂ mà không phụ thuộc vào m.

2. Ví dụ

Bài tập 1: Xét phương trình: x² - 2mx + 2m - 2 = 0

a) Xác định giá trị của m sao cho phương trình có hai nghiệm x₁, x₂

b) Tìm mối liên hệ giữa x₁ và x₂ mà không phụ thuộc vào tham số m?

Chi tiết lời giải:

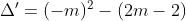
$\Delta ' = (-m)^{2} - (2m - 2)$

= m² - 2m + 2

= m² - 2m + 1 + 1

= (m - 1) + 1 > 0 với mọi giá trị của m

→ Phương trình luôn có hai nghiệm phân biệt x₁ và x₂ cho mọi giá trị của m

$\left\{\begin{matrix} x_{1} + x_{2} = 2m & \\ x_{1}x_{2} = 2m - 1 & \end{matrix}\right.$

Thay 2m = x₁ + x₂ vào phương trình thứ hai, ta có: x₁x₂ = x₁ + x₂ - 1

Bài 2: Cho phương trình x² - 2(m - 1)x + m - 3 = 0 (với m là tham số). Xác định một công thức liên hệ giữa hai nghiệm của phương trình mà không phụ thuộc vào m.

Giải chi tiết:

$\Delta ' = \left[ -(m-1) ^{2} \right] - 1 \cdot (m-3)$

= m² - 3m + 4

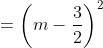
Do đó, phương trình đã cho luôn có hai nghiệm phân biệt x₁ và x₂.

Áp dụng hệ thức Viète, ta có:

$\left\{\begin{matrix} x_{1} + x_{2} = 2(m - 1) & \\ x_{1}x_{2} = m - 3 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x_{1} + x_{2} = 2m - 2 \text{ (1)} & \\ x_{1}x_{2} = m - 3 \text{ (2)} \end{matrix}\right.$

Trừ (2) khỏi (1): x₁ + x₂ - 2x₁x₂ = 4, không phụ thuộc vào m.

Bài 3: Xét phương trình 2x² + (2m - 1)x + m - 1 = 0 (với m là tham số). Tìm một công thức liên hệ giữa hai nghiệm của phương trình này mà không phụ thuộc vào m.

Lời giải chi tiết:

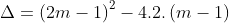
$\Delta = \left(2m - 1\right)^{2} - 4 \cdot 2 \cdot (m - 1)$

= 4m² - 4m + 1 - 8m + 8

= 4m² - 12m + 9

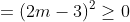
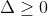$= \left(2m - 3\right)^{2} \geq 0$ $\Delta \geq 0$ ₁₂

Áp dụng hệ thức Vi-et, ta có:

$\left\{\begin{matrix} x_{1} + x_{2} = \frac{1 - 2m}{2} & \\ x_{1}x_{2} = \frac{m - 1}{2} & \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} 2\left ( x_{1} + x_{2}\right ) = 1 - 2m & \\ 2x_{1} x_{2} = m - 1 & \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} 2(x_{1} + x_{2}) = 1 - 2m \quad (1) & \\ 4x_{1}x_{2} = 2m - 2 \quad (2) & \end{matrix}\right.$

Cộng (1) và (2): 2(x₁ + x₂) + 4x₁x₂ = -1, không phụ thuộc vào m.

3. Bài tập thực hành

Bài 1: Xét phương trình 2x² + (2m - 1)x + m - 1 = 0 (m là tham số). Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình này mà không phụ thuộc vào m.

A. (x₁ + x₂) - 4x₁x₂ = -4

B. 2(x₁ + x₂) + 4x₁x₂ = 0

C. (x₁ + x₂) - x₁x₂ = 2

D. 2(x₁ + x₂) + 4x₁x₂ = -1

Giải chi tiết:

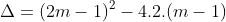
$\Delta = (2m-1)^{2} - 4 \cdot 2 \cdot (m-1)$

= 4m² - 4m + 1 - 8m + 8

= 4m² - 12m + 9

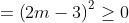
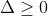
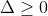$= \left(2m - 3\right)^{2} \geq 0$ $\Delta \geq 0$ $\Delta \geq 0$ ₁₂

Dựa vào hệ thức Vi-et, ta có:

$\left\{\begin{matrix} x_{1} + x_{2} = \frac{1-2m}{2} & \\ x_{1} x_{2} = \frac{m-1}{2} & \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} 2\left(x_{1} + x_{2}\right) = 1 - 2m & \\ 2x_{1}x_{2} = m - 1 & \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} 2\left(x_{1} + x_{2}\right) = 1 - 2m (1) & \\ 4x_{1}x_{2} = 2m - 2 (2) & \end{matrix}\right.$

Cộng (1) và (2): 2(x₁ + x₂) + 4x₁x₂ = -1, không phụ thuộc vào m

Vậy đáp án chính xác là D

Bài 2: Xét phương trình (m - 1)x² - 2(m + 1)x + m = 0 (m là tham số). Khi phương trình có nghiệm, hãy tìm hệ thức liên hệ giữa các nghiệm của phương trình mà không phụ thuộc vào m.

A. x₁ + x₂ - x₁x₂ = 2

B. x₁

+ x₂ + 5x₁x₂ = 7

C. x₁ + x₂ - 3x₁x₂ = -2

D. x₁ + x₂ + 5x₁x₂ = -1

Chi tiết đáp án:

Giả sử phương trình có hai nghiệm x₁ và x₂

Áp dụng hệ thức Vi-ét, ta có:

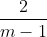
$\left\{\begin{matrix} x_{1} + x_{2} = \frac{2(m-1)}{m-1}& \\ x_{1}x_{2} = \frac{m}{m-1}& \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_{1} + x_{2} = \frac{2m}{m-1} + \frac{2}{m-1} (1)& \\ 2x_{1}x_{2} = \frac{2m}{m-1} (2)& \end{matrix}\right.$ ₁₂₁₂ $\frac{2}{m-1}$

Ngoài ra, từ:

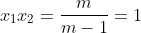
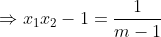
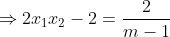
$x_{1}x_{2} = \frac{m}{m-1} = 1 + \frac{1}{m-1}$ $\Rightarrow x_{1}x_{2} - 1 = \frac{1}{m-1}$ $\Rightarrow 2x_{1}x_{2} - 2 = \frac{2}{m-1}$

Thay vào (*) ta có: x₁ + x₂ - 2x₁x₂ = 2x₁x₂ - 2, không phụ thuộc vào m

Đáp án chính xác là C

Bài 3: Xét phương trình x² - 2(m-1)x + m² - 3m = 0 (với m là tham số). Khi phương trình có nghiệm, tìm một hệ thức liên quan giữa hai nghiệm của phương trình mà không phụ thuộc vào m

A. (x₁ + x₂)² - 4x₁x₂ = 2(x₁ + x₂) = 8

B. (x₁ + x₂)² - 4x₁x₂ - 2(x₁ + x₂) = 6

C. (x₁ + x₂)² - x₁x₂ - (x₁ + x₂) = 5

D. (x₁ + x₂)² - 2x₁x₂ - 4(x₁ + x₂) = 8

Đáp án chi tiết:

Giả sử phương trình có hai nghiệm x₁ và x₂

Theo công thức Vi-ét, ta có:

$\left\{\begin{matrix} x_{1} + x_{2} = 2(m - 1) & \\ x_{1}x_{2} = m^{2} - 3m & \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} (x_{1} + x_{2})^{2} = 4(m - 1)^{2} & \\ 4x_{1}x_{2} = 4m^{2} - 12m & \end{matrix}\right.$ $\Leftrightarrow \left\{\begin{matrix} (x_{1} + x_{2})^{2} = 4m^{2} - 8m + 4 (1) & \\ 4x_{1}x_{2} = 4m^{2} - 12m (2) & \end{matrix}\right.$

Lấy (1) trừ (2): (x₁ + x₂)² - 4x₁x₂ = 4m + 4 (*)

Ngoài ra, từ: x₁ + x₂ = 2m - 2, ta có 2(x₁ + x₂) = 4m - 4, nên 2(x₁ + x₂) + 4 = 4m. Thay vào (*) ta có:

(x₁ + x₂)² - 4x₁x₂ = 2(x₁ + x₂) + 4 + 4

⇔ (x₁ + x₂)² - 4x₁x₂ - 2(x₁ + x₂) = 8 không phụ thuộc vào m

Đáp án chính xác là: A

Bài 4: Xét phương trình 2x² + (2m -1)x + m - 1 = 0 (1) với m là tham số. Gọi x₁ và x₂ là các nghiệm của phương trình (1). Tìm hệ thức liên quan giữa hai nghiệm mà không phụ thuộc vào m.

Chi tiết đáp án:

Để phương trình có hai nghiệm x₁ và x₂, ta cần:

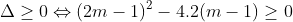
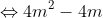
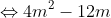
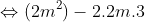
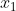
$\Delta \geq 0 \Leftrightarrow (2m -1)^{2} - 4.2(m-1) \geq 0$ $\Leftrightarrow 4m^{2} - 4m + 1 - 8m + 8 \geq 0$ $\Leftrightarrow 4m^{2} - 12m + 9 \geq 0$ $\Leftrightarrow (2m)^{2} - 2 \cdot 2m \cdot 3 + 3^{2} \geq 0$ $\Leftrightarrow (2m - 3)^{2} \geq 0$ $x_{1} + x_{2} = \frac{-(2m + 1)}{2}; x_{1}x_{2} = \frac{m - 1}{2}$

2(x_{1} + x_{2}) = -2m - 2; 2x_{1}x_{2} = m - 1

m = 2x₁x₂ + 1

Thay m = 2x₁x₂ + 1 vào phương trình (1)

2(x₁ + x₂) = -2(2x₁x₂ + 1) - 2

⇔ 2(x₁ + x₂) = -4x₁x₂ - 4

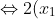
$\left\{\begin{matrix} 2(x_{1}+x_{2}) = -2m - 2 & \\ 2x_{1}x_{2}= m -1& \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2(x_{1}+ x_{2})= -2m -2 & \\ 4x_{1}x_{2}= 2m -2& \end{matrix}\right.$ $\Leftrightarrow 2(x_{1}+ x_{2}) + 4x_{1}x_{2} = -4$

Bài 5: Xét phương trình x² - 2(2m + 1)x + 3 - 4m = 0 (với m là tham số). Khi phương trình có nghiệm, xác định một hệ thức giữa hai nghiệm của phương trình không phụ thuộc vào m.

A. x₁ + x₂ - x₁x₂ = 4

B. x₁ + x₂ + x₁x₂ = 2

C. x₁ + x₂ - x₁x₂ = 5

D. x₁ + x₂ - x₁x₂ = 3

Đáp án chi tiết:

Giả sử phương trình có hai nghiệm x₁ và x₂

Áp dụng hệ thức Vi-ét, ta có:

$\left\{\begin{matrix} x_{1} + x_{2} = 2(2m + 1) & \\ x_{1}x_{2} = 3 - 4m & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x_{1} + x_{2} = 4m + 2 (1) & \\ x_{1}x_{2} = 3 - 4m (2) & \end{matrix}\right.$

Từ (1) cộng (2): x₁ + x₂ + x₁x₂ = 5, không phụ thuộc vào m

Đáp án đúng là: C

Bài 6: Xét phương trình x² - 2(2m+1)x + 3 - 4m = 0 (với m là tham số). Khi phương trình có nghiệm, xác định hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào m.

A. x₁ + x₂ - x₁x₂ = 3

B. x₁ + x₂ + x₁x₂ = 2

C. x₁ + x₂ - x₁x₂ = 4

D. x₁ + x₂ - x₁x₂ = 5

Chi tiết đáp án:

Giả thiết phương trình có hai nghiệm x₁ và x₂

Áp dụng hệ thức Vi-ét, ta có:

$\left\{\begin{matrix} x_{1} + x_{2} = 2(2m + 1) & \\ x_{1} x_{2} = 3 - 4m & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_{1} + x_{2} = 4m + 2 & \\ x_{1} x_{2} = 3 - 4m & \end{matrix}\right.$

Cộng (1) và (2): x₁ + x₂ + x₁x₂ = 5, không phụ thuộc vào m

Đáp án chính xác là A

Bài 7: Xét phương trình x² + 2(m+1)x + 2m = 0 (với m là tham số). Tìm một công thức liên kết giữa hai nghiệm của phương trình mà không phụ thuộc vào m

A. (x₁ + x₂) - x₁x₂ = -2

B. (x₁ + x₂) - 2x₁x₂ = -1

C. (x₁ + x₂) + x₁x₂ = -2

D. 2(x₁ + x₂) + x₁x₂ = 0

Chi tiết đáp án:

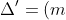
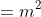
$\Delta ' = (m + 1)^{2} = 2m$ $= m^{2} + 2m + 1 - 2m$

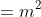
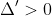₁₂

Theo định lý Viète, ta có:

$\left\{\begin{matrix} x_{1} + x_{2} = -2(m + 1)& \\ x_{1} x_{2}= 2m& \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_{1}+ x_{2} = -2m - 2 (1) & \\ x_{1}x_{2}= 2m (2) & \end{matrix}\right.$

Cộng (1) và (2): (x₁ + x₂) + x₁x₂ = -2 không phụ thuộc vào m

Đáp án chính xác là: A

4. Bài tập tự luyện

Bài 1: Xét phương trình x² - 2(m-1)x - m - 3 = 0 (với m là tham số). Tìm mối liên hệ giữa các nghiệm phân biệt x₁ và x₂ không phụ thuộc vào giá trị của m

Bài 2: Tìm mối liên hệ giữa hai nghiệm phân biệt của phương trình x² - (m +3)x + 2m - 5 = 0 mà không phụ thuộc vào m

Bài 3: Cho phương trình (m-1)x² - 2mx + m + 1 = 0, với m là tham số

a) Chứng minh phương trình có hai nghiệm phân biệt khi m khác 1

b) Tìm mối liên hệ giữa hai nghiệm phân biệt của phương trình không phụ thuộc vào m

Bài 4: Xét phương trình (m - 1)² - 2(m-4)x + m - 5 = 0 (với m là tham số)

a) Xác định giá trị của m để phương trình có hai nghiệm phân biệt x₁ và x₂

b) Tìm mối liên hệ giữa hai nghiệm x₁ và x₂ không phụ thuộc vào tham số m

Bài 5: Cho phương trình 2x² - 2(m -1)x - 2m - 3 = 0 (1) với m là tham số

a) Chứng minh phương trình (1) luôn có hai nghiệm với mọi giá trị của m

b) Trong trường hợp phương trình (1) có hai nghiệm phân biệt, xác định mối quan hệ giữa x₁ và x₂ mà không phụ thuộc vào m

Bài 6: Xét phương trình x² -(m - 3)x - 2m = 0 (1)

a) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m

b) Tìm mối liên hệ giữa các nghiệm x₁ và x₂ không phụ thuộc vào m

Bài 7: Xem xét phương trình bậc hai x: x² - 2(m+1)x + m - 4 = 0 (với m là tham số)

a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt x₁ và x₂ cho mọi giá trị của m

b) Xác định mối quan hệ giữa hai nghiệm phân biệt của phương trình mà không phụ thuộc vào giá trị của m

Bài 8: Xét phương trình bậc hai: x² -2(m+4)x + m² - 8 = 0 (1) với m là tham số

a) Tìm giá trị của m sao cho phương trình (1) có hai nghiệm phân biệt x₁ và x₂

b) Xác định mối liên hệ giữa hai nghiệm phân biệt của phương trình (1) mà không phụ thuộc vào m

Các câu hỏi thường gặp

Cách xác định mối quan hệ giữa x1 và x2 trong phương trình bậc hai là gì?

Để xác định mối quan hệ giữa x1 và x2, cần áp dụng định lý Viète, từ đó rút ra hệ thức mà không phụ thuộc vào tham số m. Phương pháp này cho phép chúng ta hiểu rõ hơn về các nghiệm của phương trình.

Các bước giải quyết bài tập xác định mối quan hệ giữa x1 và x2 như thế nào?

Đầu tiên, loại bỏ tham số m ra khỏi hệ phương trình, sau đó áp dụng các công thức liên hệ như Viète để tìm ra mối quan hệ giữa x1 và x2 mà không cần biết giá trị của m.

Tại sao phải tìm mối liên hệ giữa các nghiệm không phụ thuộc vào m?

Việc tìm mối liên hệ giữa các nghiệm không phụ thuộc vào m giúp chúng ta hiểu rõ hơn về bản chất của phương trình bậc hai. Điều này cũng rất quan trọng trong việc giải quyết các bài toán thực tế liên quan đến toán học.

Có thể sử dụng hệ thức Viète trong mọi trường hợp không?

Có, hệ thức Viète có thể áp dụng cho mọi phương trình bậc hai để tìm ra mối liên hệ giữa các nghiệm x1 và x2. Tuy nhiên, cần đảm bảo rằng phương trình có hai nghiệm phân biệt.

Điều kiện nào để phương trình bậc hai có hai nghiệm phân biệt?

Phương trình bậc hai có hai nghiệm phân biệt khi delta (Δ) lớn hơn 0. Cụ thể, điều này có nghĩa là hệ số của x và hằng số trong phương trình phải đáp ứng một số điều kiện nhất định.

Nội dung từ Mytour nhằm chăm sóc khách hàng và khuyến khích du lịch, chúng tôi không chịu trách nhiệm và không áp dụng cho mục đích khác.

Nếu bài viết sai sót hoặc không phù hợp, vui lòng liên hệ qua email: [email protected]