| Thuật toán tìm kiếm theo chiều sâu | |
| Ví dụ về thứ tự duyệt theo chiều sâu | |
| Phân loại | Thuật toán tìm kiếm |
| Cấu trúc dữ liệu | Đồ thị |
| Độ phức tạp thời gian | O(|V|+|E|) với đơn đồ thị, không duyệt vòng
|
| Độ phức tạp không gian | O(|V|) nếu duyệt toàn bộ đồ thị, mỗi đỉnh qua đúng một lần |
| Thuật toán tìm kiếm cây và đồ thị |
|---|
|
| Danh sách |
|
| Liên quan |
|
Khám phá ưu tiên theo chiều sâu hoặc khám phá theo chiều sâu (tiếng Anh: Depth-first search - DFS) là một thuật toán được sử dụng để duyệt qua hoặc tìm kiếm trong cây hoặc đồ thị. Thuật toán bắt đầu từ đỉnh gốc (hoặc chọn một đỉnh nào đó làm gốc) và mở rộng xa nhất có thể theo mỗi nhánh.
Thường thì, DFS là một kiểu tìm kiếm không hoàn chỉnh, trong đó quá trình tìm kiếm được tiếp tục tới đỉnh con đầu tiên của nút đang được kiểm tra cho đến khi tìm thấy đỉnh mục tiêu hoặc đến một nút không còn con. Sau đó, thuật toán quay lại đỉnh trước đó để tiếp tục tìm kiếm. Trong dạng không đệ quy, các đỉnh chờ được phát triển được lưu trữ trong một ngăn xếp theo cấu trúc LIFO.
Độ phức tạp về không gian của DFS thấp hơn so với BFS (tìm kiếm theo chiều rộng). Tuy nhiên, độ phức tạp thời gian của hai thuật toán là tương đương và bằng O(|V| + |E|).
Ví dụ
Khi thực hiện tìm kiếm ưu tiên chiều sâu, ta bắt đầu từ đỉnh A, đi theo cạnh trái, hoàn thành việc khám phá cây con trái trước khi chuyển sang cây con phải. Thứ tự các đỉnh được thăm là: A, B, D, F, E, C, G.
Quá trình thăm các đỉnh diễn ra như sau: Sau khi thăm đỉnh A, vì B chưa được khám phá, ta đi theo cạnh AB để thăm B, tiếp tục theo cạnh BD để đến D. Vì D không còn đỉnh con để thăm, ta quay lại B. Từ B, ta đi theo cạnh BF đến F, tiếp tục theo cạnh FE để thăm E. Do E không còn đỉnh con để tiếp tục, ta quay lại A và tiếp tục thăm C, G.
Kết quả của thuật toán
Kết quả tự nhiên của thuật toán tìm kiếm theo chiều sâu là một cây phủ qua tất cả các đỉnh đã được duyệt trong đồ thị.
Duyệt các đỉnh
Phương pháp này có thể được áp dụng để tạo ra một danh sách tuần tự các đỉnh trong một đồ thị (hoặc cây). Có ba cách để thực hiện phương pháp này:
- Duyệt theo thứ tự trước (preordering): sinh ra danh sách mà trong đó các đỉnh xuất hiện theo trật tự đúng như khi thuật toán thăm đến. Đây là cách biểu diễn tự nhiên của thuật toán tìm kiếm theo chiều sâu. Ký pháp trước được gọi là tiền tố.
- Duyệt theo thứ tự sau (postordering): sinh ra danh sách mà các đỉnh xuất hiện theo thứ tự của lần thăm cuối cùng khi thực hiện thuật toán. Duyệt theo thứ tự sau của một cây biểu thức sẽ tạo ra ký pháp hậu tố.
- Duyệt theo thứ tự ngược sau (reverse postordering): kết quả của cách duyệt này là sự đảo ngược thứ tự kết quả của duyệt theo thứ tự sau. Thông thường, khi duyệt cây, cách này cho kết quả giống với duyệt trước, nhưng với đồ thị, duyệt trước và ngược sau có thể cho kết quả khác nhau. Đối với đồ thị có hướng và không có vòng, duyệt ngược sau cho ra một thứ tự tô-pô của đồ thị.
Thuật toán tìm kiếm theo chiều sâu trên đồ thị không có hướng
Ý tưởng của thuật toán
- Thuật toán DFS trên đồ thị không có hướng tương tự như việc khám phá mê cung với một cuộn chỉ và một thùng sơn đỏ để đánh dấu, tránh bị lạc. Mỗi đỉnh s trong đồ thị đại diện cho một cửa trong mê cung.
- Bắt đầu từ đỉnh s, buộc đầu cuộn chỉ vào s và đánh dấu đỉnh này là 'đã thăm'. Sau đó, đánh dấu s là đỉnh hiện tại u.
- Nếu chúng ta đi theo cạnh (u,v) bất kỳ.
- Nếu cạnh (u,v) dẫn đến đỉnh 'đã thăm' v, quay lại u.
- Nếu đỉnh v chưa được thăm, di chuyển đến v và cuộn chỉ theo. Đánh dấu v là 'đã thăm'. Đặt v thành đỉnh hiện tại và lặp lại quy trình.
- Khi đến một đỉnh mà tất cả các cạnh kề đều dẫn đến các đỉnh 'đã thăm', quay lui bằng cách cuộn ngược chỉ và trở lại cho đến khi gặp một đỉnh kề với cạnh chưa thăm. Tiếp tục quy trình như trước.
- Khi trở về s và không còn cạnh nào kề chưa được thăm, thuật toán DFS kết thúc.
Mệnh đề
Nếu ta thực hiện thuật toán DFS trên đồ thị vô hướng G với đỉnh bắt đầu là s, thì:
- Thuật toán sẽ thăm tất cả các đỉnh thuộc cùng thành phần liên thông với s.
- Các cạnh được đánh dấu là 'đã thăm' sẽ tạo nên một cây bao trùm của thành phần liên thông chứa s.
Chứng minh
- Khẳng định 1 là rõ ràng vì DFS sẽ duyệt qua tất cả các đỉnh kề của đỉnh hiện tại (có thể chứng minh bằng cách phản chứng).
- Khẳng định 2 đúng vì ta chỉ đánh dấu các cạnh đi đến những đỉnh mới, do đó không thể tạo ra chu trình. Vì vậy, DFS tạo ra một cây. Hơn nữa, DFS thăm tất cả các đỉnh thuộc thành phần liên thông nên cây này là cây bao trùm tối đại.
Độ phức tạp của thuật toán
- DFS được gọi chính xác 1 lần cho mỗi đỉnh.
- Mỗi cạnh được kiểm tra đúng 2 lần, mỗi lần từ một đỉnh kề.
- Với ns đỉnh và ms cạnh trong thành phần liên thông chứa s, một phép DFS bắt đầu từ s sẽ có thời gian thực hiện là O(ns + ms) nếu:
- Đồ thị được biểu diễn bằng danh sách kề.
- Đánh dấu một đỉnh là 'đã thăm' và kiểm tra trạng thái của đỉnh 'đã thăm' có chi phí là O(degree).
- Khi các đỉnh được đánh dấu là 'đã thăm', ta có thể kiểm tra hệ thống các cạnh kề với đỉnh hiện tại mà không kiểm tra một cạnh quá một lần.
Xác định các đỉnh kề trong DFS
- Kết quả của DFS phụ thuộc vào cách chọn đỉnh kế tiếp.
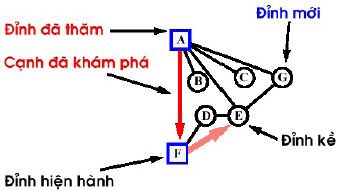
- Bắt đầu từ A và thử nối đến F, sau đó đến B, rồi E, C, và cuối cùng đến G sẽ cho kết quả:
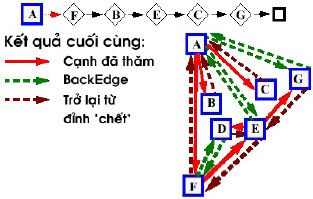
- Nếu bắt đầu từ A nhưng theo một thứ tự khác, các cạnh đã thăm, backedge và các đỉnh đệ quy sẽ thay đổi.
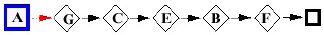
Thực hiện từng bước của thuật toán
Bây giờ, chúng ta sẽ tiến hành từng bước của thuật toán dựa trên ví dụ đã nêu.
Nguyên lý
Bắt đầu từ một đỉnh, di chuyển theo các cạnh xa nhất có thể. Sau đó quay lại đỉnh của cạnh xa nhất và tiếp tục theo cách tương tự cho đến khi đạt đến đỉnh cuối cùng.
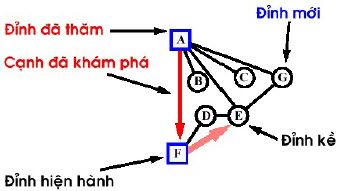
- Giai đoạn 1:
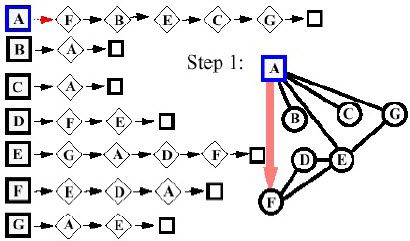
- Giai đoạn 2:
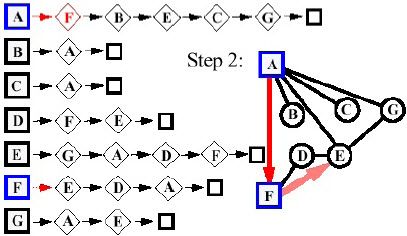
- Giai đoạn 3:
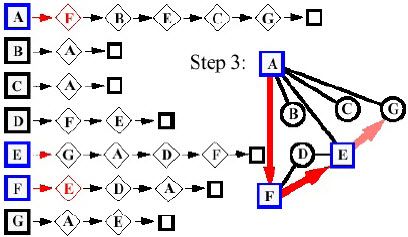
- Giai đoạn 4:
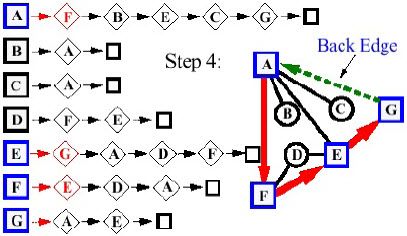
- Giai đoạn 5:
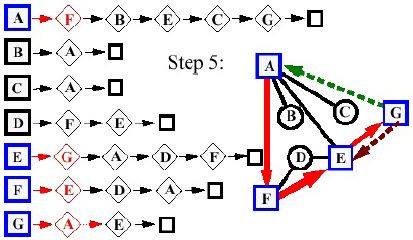
- Giai đoạn 6:
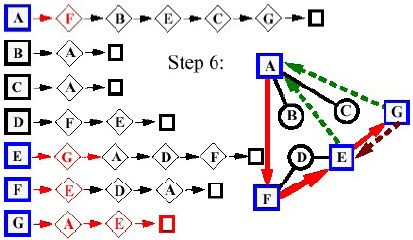
- Giai đoạn 7:
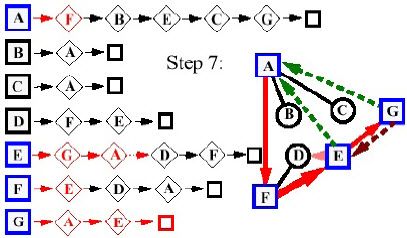
- Giai đoạn 8:
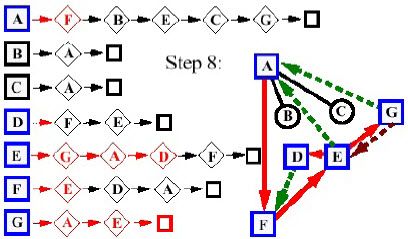
- Giai đoạn 9:
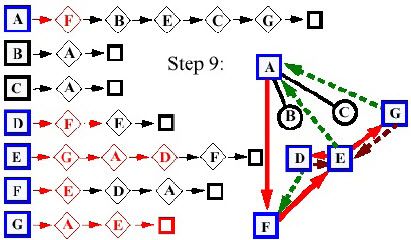
- Giai đoạn 10:
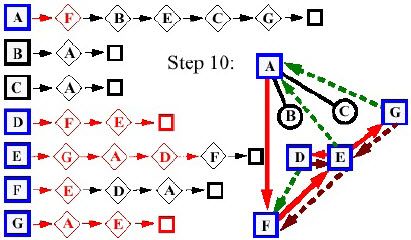
- Giai đoạn 11:
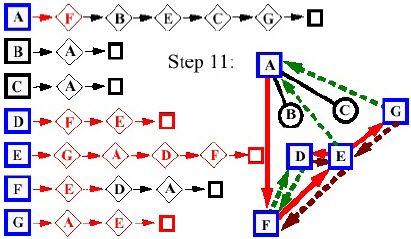
- Giai đoạn 12:
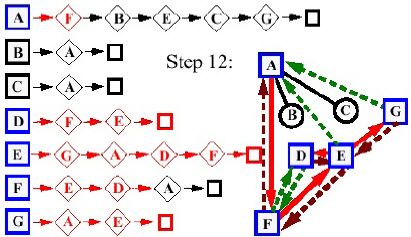
- Giai đoạn 13:
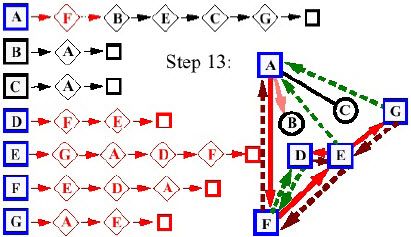
- Giai đoạn 14:
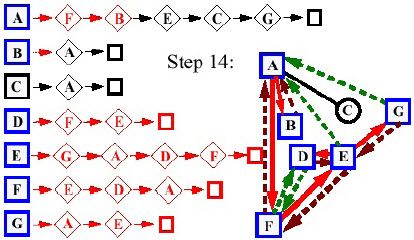
- Giai đoạn 15:
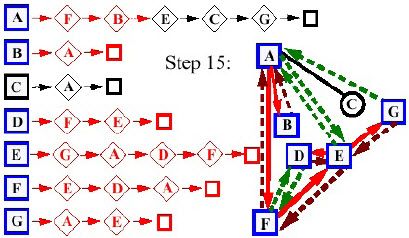
- Giai đoạn 16:
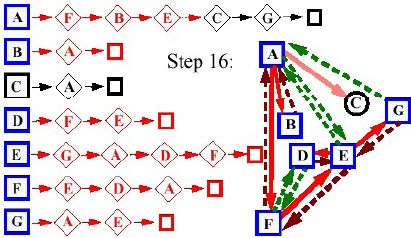
- Giai đoạn 17:
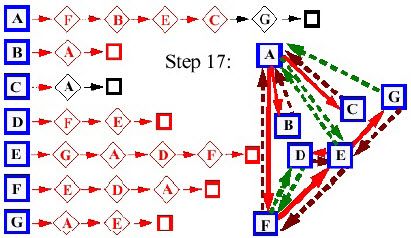
- Giai đoạn 18:
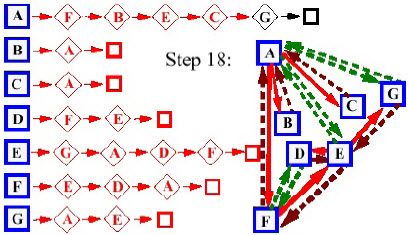
- Bước 19:
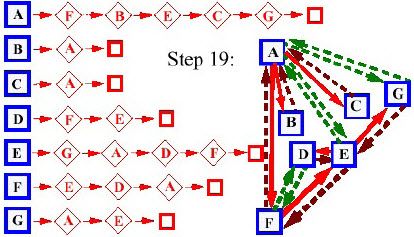
Ứng dụng
Nhiều giải thuật sử dụng tìm kiếm theo chiều sâu:
- Nhận diện các thành phần liên thông trong đồ thị
- Xếp hạng tô-pô cho đồ thị
- Xác định các thành phần liên thông mạnh của đồ thị có hướng
- Xem xét liệu đồ thị có phải là đồ thị phẳng hay không
Tìm kiếm theo chiều rộng
