Khám phá tiêu điểm, tiêu cự, tâm sai, trục lớn và trục nhỏ của elip

Trong chương trình Toán lớp 10, chúng ta sẽ học về hình elip. Bài viết này cung cấp những kiến thức quan trọng về tiêu điểm, tiêu cự, tâm sai, trục lớn và trục nhỏ của elip. Xin mời bạn tham khảo!

1. Tổng quan lý thuyết

- Với hai điểm cố định F₁ và F₂ cùng một độ dài không đổi 2a lớn hơn khoảng cách F₁F₂, elip là tập hợp các điểm M trên mặt phẳng sao cho tổng khoảng cách từ M đến F₁ và F₂ luôn bằng 2a.

- Các yếu tố của elip: elip (E) có phương trình x² / a² + y² / b² = 1

+ Hai tiêu điểm: F₁(-c;0) và F₂(c;0)

+ Bốn đỉnh: A₁(-a;0), A₂(a;0), B₁(0;-b) và B₂(0;b)

+ Độ dài trục lớn: A₁A₂ = 2a

+ Độ dài trục nhỏ: B₁B₂ = 2b

+ Khoảng cách giữa hai tiêu điểm: F₁F₂ = 2c

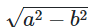
2. Các công thức cơ bản

Cho elip (E) với phương trình x² / a² + y² / b² = 1

- Trục chính của (E) nằm trên trục hoành: A₁A₂ = 2a

- Trục phụ của (E) nằm trên trục tung: B₁B₂ = 2b

_{MộtHai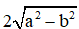BaBốn}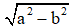

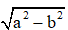
3. Ví dụ cụ thể

Bài tập 1: Xác định tọa độ các trục, tiêu điểm, tiêu cự và độ lệch tâm của elip (E) với phương trình: x² / 16 + y² / 9 = 1

Giải đáp

Xem xét phương trình của elip (E): x² / 16 + y² / 9 = 1. Ta có:

a² = 16 => a = 4

b² = 9 => b = 3

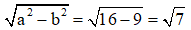
Từ đây ta có:

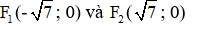
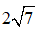
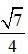
Trục chính của elip (E) nằm trên trục Ox: A₁A₂ = 2. 4 = 8

Trục phụ của elip (E) nằm trên trục Oy: B₁B₂ = 2. 3 = 6

Bài tập 2: Cho elip với phương trình x² / 100 + y² / 36 = 1. Xác định tiêu điểm, tiêu cự, độ lệch tâm, trục chính và trục phụ của elip.

Giải đáp:

Xem xét phương trình elip: x² / 100 + y² / 36 = 1, ta có:

a² = 100 => a = 10

b² = 36 => b = 6

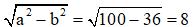
Từ đó, ta có:

Tiêu điểm của elip (E) là: F₁(-8;0) và F₂(8;0)

Tiêu cự của elip (E) là: F₁F₂ = 2. 8 = 16

Độ lệch tâm của elip (E) là: e = 8 / 10 = 4 / 5

Trục chính của elip (E) nằm trên trục Ox: A₁A₂ = 2.10 = 20

Trục phụ của elip (E) nằm trên trục Oy: B₁B₂ = 2.6 = 12

Bài tập 3: Cho elip với phương trình x² / 36 + y² / 25 = 1. Xác định tiêu điểm, tiêu cự, độ lệch tâm, trục chính và trục phụ của elip.

Giải đáp:

Xem xét phương trình elip: x² / 36 + y

² / 25 = 1, ta có:

a² = 36 => a = 6

b² = 25 => b = 5

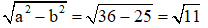
Từ đó, ta có:

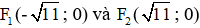₁₂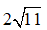

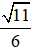
Trục lớn của Elip (E) nằm trên trục Ox với A₁A₂ = 2.6 = 12

Trục nhỏ của Elip (E) nằm trên trục Oy với B₁B₂ = 2.5 = 10

4. Bài tập thực hành

Bài 1. Xác định tọa độ của các tiêu điểm; tọa độ các đỉnh; chiều dài trục lớn và trục nhỏ của các elip sau đây:

a) x² / 169 + y²/ 25 = 1

b) x² + 4y² = 1

Giải pháp:

a) x² / 169 + y² / 25 = 1 tương đương với x² / 13² + y² / 5² = 1

Phương trình của Elip có dạng: x² / a² + y² / b² = 1

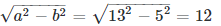
Các tọa độ của đỉnh Elip là: A₁ (-13;0); A₂ (13;0); B₁(0;-5); B₂(0;5)

Các tọa độ của tiêu điểm Elip là: F₁(-12;0); F₂(12;0)

Chiều dài của trục lớn là 2a = 26; chiều dài của trục nhỏ là 2b = 10.

b) x² + 4y² = 1

²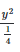

Phương trình của elip có dạng: x² / a² + y² / b² = 1

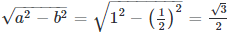
Các đỉnh của Elip là: A₁(-1;0); A₂(1;0); B₁(0;-1/2); B₂(0;1/2)

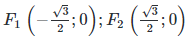
Chiều dài của trục lớn là 2a = 2; chiều dài của trục nhỏ là 2b = 1

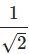
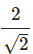
C. 1 / 3

D. 1

Cách giải quyết:

Tính tỷ số e = c / a, trong đó:

+) 2c là khoảng cách giữa các tiêu điểm của elip

+) 2a là chiều dài trục lớn của elip

+) 2b là chiều dài trục nhỏ của elip

Và chúng ta có a² = b² + c²

Kết quả: 

Trong elip, chiều dài trục nhỏ bằng khoảng cách giữa các tiêu điểm, vì vậy ta có b = c

²²²²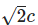

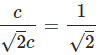
Do đó, chọn đáp án A

Bài 3. Cho elip (E) với tiêu cự là 2c, và chiều dài trục lớn và trục nhỏ lần lượt là 2a và 2b. Trong số các mệnh đề dưới đây, mệnh đề nào là đúng?

A. c < b < a

B. c < a < b

C. c > b > a

D. c < a và b < a

Cách giải: 

Áp dụng lý thuyết về phương trình chuẩn của elip

Phương trình chuẩn của elip có dạng: x² / a² + y² / b² = 1 với điều kiện a > b > c và a² = b² + c², trong đó 2c là khoảng cách giữa các tiêu điểm của (E)

Kết quả:

Vì a² = b² + c² và a, b, c > 0 nên a² > c² <=> a > c. Hiển nhiên, b < a. Do đó, chọn đáp án D

Bài 4. Cho elip (E) với hai tiêu điểm là F1 và F2, có chiều dài trục lớn là 2a. Trong số các mệnh đề dưới đây, mệnh đề nào là chính xác?

A. 2a = khoảng cách F1F2

B. 2a > khoảng cách F1F2

C. 2a < khoảng cách F1F2

D. 4a = khoảng cách F1F2

Phương pháp giải:

Áp dụng lý thuyết về phương trình chuẩn của elip

Phương trình chuẩn của elip có dạng: x² / a² + y² / b² = 1, với a > b > 0 và a² = b² + c², trong đó 2c là khoảng cách giữa hai tiêu điểm của elip

Lời giải:

Elip (E) có hai tiêu điểm F1 và F2, do đó 2c = khoảng cách F1F2

Vì a² = b² + c² và a, b, c > 0, ta có a² > c² <=> a > c. Do đó, 2a > khoảng cách F1F2

Chọn đáp án B

Bài 5. Xét elip (E) với phương trình x² + 4y² - 40 = 0. Tính chu vi của hình chữ nhật cơ sở là:

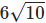
B. 10

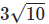
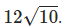
Cách giải: Tính toán từ phương trình (E) để tìm trục lớn 2a và trục bé 2b. Chu vi của hình chữ nhật cơ sở được tính bằng 2(2a + 2b)

Kết quả:

Phương trình elip (E) có dạng: x² + 4y² = 40

<=> x² + 4y² - 40 = 0 <=> x² / 40 + y² / 40 = 1

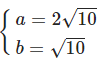
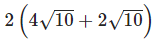
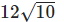
Chọn đáp án D

Bài 6. Phương trình chính tắc của elip có tiêu điểm F1 (-1; 0), F2 (1; 0) và tâm sai e = 1 / 5 là:

A. x² / 24 + y² / 25 = 1

B. x² / 24 + y² / 25 = -1

C. x² / 25 + y² / 24 = 1

D. x² / 25 + y² / 24 = -1

Cách giải:

Phương trình chính tắc của elip có dạng: x² / a² + y² / b² = 1. Xác định a và b

- Elip có 4 đỉnh tại A1 (-a;0), A2 (a;0), B1 (0;-b), B2 (0;b)

- Elip có tiêu cự bằng 2c, và có mối quan hệ a² = b² + c²

Đáp án là:

Elip có hai tiêu điểm F1(-1;0), F2(1;0) nên c = 1

Elip có tâm sai e = 1/5 nên c / a = 1 / 5, dẫn đến a = 5

Theo đó, b² = a² - c² = 25 - 1 = 24

Vậy phương trình của elip là: x² / 25 + y² / 24 = 1

Chọn đáp án C

Bài 7: Xem elip (E): x² / 25 + y² / 9 = 1 và các mệnh đề sau đây:

1. Elip (E) có các tiêu điểm tại F1(0;-4) và F2(0;4)

2. Tỉ số c / a của elip (E) là 4 / 5

3. Đỉnh A1 của elip (E) nằm tại (-5;0)

4. Độ dài trục nhỏ của elip (E) là 3

Xác định mệnh đề sai trong các mệnh đề trên:

A. Mệnh đề 1 và 2

B. Mệnh đề 2 và 3

C. Mệnh đề 1 và 3

D. Mệnh đề 4 và 1

²²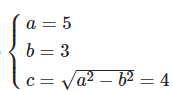

Kết luận được rằng:

1. Elip (E) có các tiêu điểm tại F1(-4;0) và F2(4;0), vì vậy (1) là sai

2. Elip (E) có tỉ số c / a là 4 / 5, do đó (2) là đúng

3. Elip (E) có đỉnh A₁(-5;0), vì thế (3) là đúng

4. Elip (E) có độ dài trục nhỏ là 2b = 6, do đó (4) là sai

Vậy các mệnh đề sai là (1) và (4)

Chọn đáp án D

Bài 8: Phương trình chính tắc của elip với trục lớn dài 12 và tiêu cự 10 là:

A. x² / 36 + y² / 9 = 1

B. x² / 36 + y² / 25 = 1

C. x² / 36 + y² / 11 = 1

D. x² / 36 + y² / 10 = 1

Đáp án:

Độ dài trục lớn là 12, từ đó suy ra 2a = 12, vậy a = 6

Tiêu cự là 10, do đó 2c = 10, dẫn đến c = 5

Theo công thức a² = b² + c², ta tính được b² = a² - c² = 36 - 25 = 11

Chọn đáp án C

Bạn đọc có thể tham khảo bài viết: Đề thi giữa học kì 2 môn Toán 10 sách Cánh Diều có đáp án