Đọc về cách tính này có thể được sử dụng cho kiểm định giả thuyết trong thống kê
Khái Niệm về Kiểm Định T là gì?
Kiểm định T là một phép thống kê suy luận được sử dụng để xác định xem có sự khác biệt đáng kể giữa hai nhóm và cách họ tương quan với nhau hay không. Kiểm định T được sử dụng khi các tập dữ liệu tuân theo phân phối chuẩn và có phương sai không biết, như tập dữ liệu ghi lại từ việc tung đồng xu 100 lần.
Kiểm định t là một phép kiểm định giả thuyết trong thống kê và sử dụng thống kê t, các giá trị phân phối t, và bậc tự do để xác định ý nghĩa thống kê.
Nhận Điểm Chính
- Phép kiểm định T là một phép thống kê suy luận được sử dụng để xác định xem có sự khác biệt đáng kể thống kê giữa hai biến.
- Kiểm định T là một phép kiểm định giả thuyết trong thống kê.
- Việc tính toán kiểm định T yêu cầu ba giá trị dữ liệu cơ bản bao gồm sự khác biệt giữa các giá trị trung bình từ mỗi tập dữ liệu, độ lệch chuẩn của mỗi nhóm, và số lượng giá trị dữ liệu.
- Kiểm định T có thể phụ thuộc hoặc độc lập.

Mytour / Sabrina Jiang
Hiểu về Kiểm Định T
Kiểm định T so sánh các giá trị trung bình của hai tập dữ liệu và xác định xem chúng có đến từ cùng một quần thể hay không. Trong các ví dụ trên, một mẫu học sinh từ lớp A và một mẫu học sinh từ lớp B không có khả năng có cùng giá trị trung bình và độ lệch chuẩn. Tương tự, các mẫu được lấy từ nhóm kiểm soát được cung cấp placebo và nhóm được kê đơn thuốc nên có giá trị trung bình và độ lệch chuẩn khác nhau một chút.
Toán học, kiểm định T lấy một mẫu từ mỗi tập hợp và xác định tình trạng vấn đề. Nó giả định một giả thuyết không chứng minh rằng hai giá trị trung bình là bằng nhau.
Sử dụng các công thức, các giá trị được tính toán và so sánh với các giá trị tiêu chuẩn. Giả thuyết không chứng minh được chấp nhận hoặc bác bỏ tùy thuộc vào điều kiện. Nếu giả thuyết không chứng minh đủ điều kiện để bị bác bỏ, điều đó chỉ ra rằng các đọc số liệu dữ liệu mạnh mẽ và có thể không phải do sự tình cờ.
Kiểm định T chỉ là một trong nhiều phép kiểm định được sử dụng cho mục đích này. Nhà thống kê sử dụng các phép kiểm định bổ sung ngoài kiểm định T để xem xét nhiều biến số hơn và kích thước mẫu lớn hơn. Đối với kích thước mẫu lớn, nhà thống kê sử dụng kiểm định z. Các phương pháp kiểm định khác bao gồm kiểm định chi bình phương và kiểm định f.
Sử Dụng Kiểm Định T
Giả sử một nhà sản xuất thuốc thử nghiệm một loại thuốc mới. Theo quy trình tiêu chuẩn, thuốc được đưa cho một nhóm bệnh nhân và một placebo cho một nhóm khác được gọi là nhóm kiểm soát. Placebo là một chất không có giá trị điều trị và phục vụ như một điểm chuẩn để đo lường cách nhóm khác, được kê đơn thuốc thực sự, phản ứng.
Sau thử nghiệm thuốc, các thành viên của nhóm kiểm soát được cung cấp placebo báo cáo một tăng trưởng tuổi thọ trung bình ba năm, trong khi các thành viên của nhóm được kê đơn thuốc mới báo cáo một tăng trưởng tuổi thọ trung bình là bốn năm.
Quan sát ban đầu cho thấy thuốc đang hoạt động. Tuy nhiên, cũng có khả năng quan sát có thể do sự tình cờ. Một kiểm định T có thể được sử dụng để xác định xem kết quả có chính xác và áp dụng cho toàn bộ quần thể không.
Khi sử dụng kiểm định T, ta đặt ra bốn giả định. Dữ liệu thu thập phải tuân theo một thang đo liên tục hoặc thứ bậc, chẳng hạn như điểm số của một bài kiểm tra IQ, dữ liệu được thu thập từ một phần được chọn ngẫu nhiên của tổng dân số, dữ liệu sẽ dẫn đến một phân phối chuẩn của một đường cong hình chuông, và phương sai bằng nhau hoặc đồng nhất tồn tại khi các biến thể chuẩn bằng nhau.
Công Thức Kiểm Định T
Tính toán một kiểm định T đòi hỏi ba giá trị dữ liệu cơ bản. Chúng bao gồm sự khác biệt giữa các giá trị trung bình từ mỗi tập dữ liệu, hoặc sự khác biệt trung bình, độ lệch chuẩn của mỗi nhóm, và số lượng giá trị dữ liệu của mỗi nhóm.
So sánh này giúp xác định tác động của sự tình cờ lên sự khác biệt và xem liệu sự khác biệt đó nằm ngoài phạm vi của sự tình cờ. Kiểm định T đặt câu hỏi liệu sự khác biệt giữa các nhóm có đại diện cho một sự khác biệt thực sự trong nghiên cứu hay chỉ là một sự khác biệt ngẫu nhiên.
Kiểm định T sản sinh hai giá trị làm đầu ra của nó: giá trị t và bậc tự do. Giá trị t, hoặc điểm t, là tỷ lệ giữa sự khác biệt giữa giá trị trung bình của hai tập mẫu và sự biến thiên tồn tại trong các tập mẫu.
Giá trị tử số là sự khác biệt giữa giá trị trung bình của hai tập mẫu. Mẫu số là sự biến thiên tồn tại trong các tập mẫu và là một phép đo của sự phân tán hoặc biến động.
Giá trị t tính toán sau đó được so sánh với một giá trị thu được từ bảng giá trị ngưỡng gọi là bảng phân phối T. Các giá trị cao của điểm t cho thấy một sự khác biệt lớn tồn tại giữa hai tập mẫu. Càng nhỏ giá trị t, càng nhiều sự tương đồng tồn tại giữa hai tập mẫu.
Điểm T
Một giá trị t lớn, hoặc giá trị t, cho thấy các nhóm khác biệt trong khi một giá trị t nhỏ cho thấy các nhóm tương tự.
Bậc Tự Do đề cập đến các giá trị trong một nghiên cứu có sự tự do biến đổi và là quan trọng để đánh giá tính quan trọng và tính hợp lệ của giả thuyết không chứng minh. Việc tính toán các giá trị này thường phụ thuộc vào số lượng bản ghi dữ liệu có sẵn trong tập mẫu.
Kiểm Định T Mẫu Ghép
Kiểm định t tương quan, hay còn gọi là kiểm định t đôi, là loại kiểm định phụ thuộc và được thực hiện khi mẫu bao gồm các cặp phần tử tương tự, hoặc khi có các trường hợp đo lặp lại. Ví dụ, có thể có các trường hợp mà cùng một bệnh nhân được kiểm tra trước và sau khi nhận một liệu pháp cụ thể. Mỗi bệnh nhân được sử dụng như một mẫu điều khiển so với chính họ.
Phương pháp này cũng áp dụng cho các trường hợp mẫu có mối quan hệ hoặc có các đặc điểm tương đồng, như phân tích so sánh liên quan đến trẻ em, phụ huynh hoặc anh chị em.
Công thức tính giá trị t và bậc tự do cho kiểm định t đôi là:
Kiểm định t có phương sai bằng nhau hoặc gộp
thông tin kết quả
Kiểm định t dùng để so sánh hai trung bình độc lập và được sử dụng khi số lượng mẫu trong mỗi nhóm bằng nhau hoặc phương sai của hai tập dữ liệu tương đồng.
Công thức tính giá trị t và bậc tự do cho kiểm định t có phương sai bằng nhau là:
Tính giá trị T bằng cách lấy trung bình mẫu 1 trừ trung bình mẫu 2 chia cho căn bậc tự do, trong đó:
và,
Bậc tự do bằng tổng số quan sát của cả hai mẫu trừ 2.
Kiểm Định T-Test Phương Sai Bất Đẳng
Kiểm định t-test phương sai bất đẳng là một kiểm định t-test độc lập và được sử dụng khi số lượng mẫu trong mỗi nhóm khác nhau và phương sai của hai tập dữ liệu cũng khác nhau. Kiểm định này cũng được gọi là kiểm định t của Welch.
Công thức được sử dụng để tính giá trị t và bậc tự do cho kiểm định t-test phương sai bất đẳng là:
T-value = (trung bình 1 - trung bình 2) / căn bậc hai của ((phương sai 1 / n1) + (phương sai 2 / n2))
trong đó:
Cấp tự do
Sử dụng Kiểm định T nào?
Biểu đồ luồng sau đây có thể được sử dụng để xác định kiểm định t nào phù hợp dựa trên các đặc điểm của các tập hợp mẫu. Các yếu tố chính cần xem xét bao gồm sự tương đồng của các bản ghi mẫu, số lượng bản ghi dữ liệu trong mỗi tập hợp mẫu và phương sai của mỗi tập hợp mẫu.
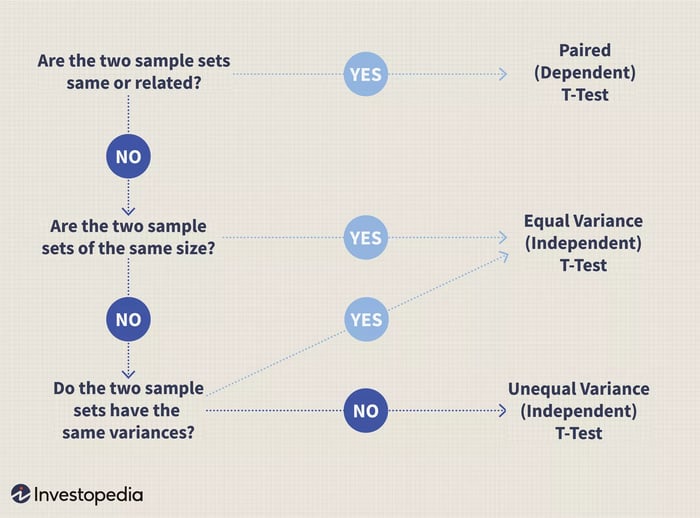
Ví dụ về Kiểm định T với Phương sai không bằng nhau
Giả sử rằng đo đường chéo của các bức tranh nhận được trong một phòng trưng bày nghệ thuật. Một nhóm mẫu bao gồm 10 bức tranh, trong khi nhóm kia bao gồm 20 bức tranh. Các tập hợp dữ liệu, với giá trị trung bình và phương sai tương ứng, như sau:
| Set 1 | Set 2 | |
|---|---|---|
| 19.7 | 28.3 | |
| 20.4 | 26.7 | |
| 19.6 | 20.1 | |
| 17.8 | 23.3 | |
| 18.5 | 25.2 | |
| 18.9 | 22.1 | |
| 18.3 | 17.7 | |
| 18.9 | 27.6 | |
| 19.5 | 20.6 | |
| 21.95 | 13.7 | |
| 23.2 | ||
| 17.5 | ||
| 20.6 | ||
| 18 | ||
| 23.9 | ||
| 21.6 | ||
| 24.3 | ||
| 20.4 | ||
| 23.9 | ||
| 13.3 | ||
| Mean | 19.4 | 21.6 |
| Variance | 1.4 | 17.1 |
Mặc dù giá trị trung bình của Tập hợp 2 cao hơn so với Tập hợp 1, nhưng chúng ta không thể kết luận rằng quần thể tương ứng với Tập hợp 2 có giá trị trung bình cao hơn quần thể tương ứng với Tập hợp 1.
Sự khác biệt từ 19,4 đến 21,6 có phải chỉ do may mắn mà thôi, hay có sự khác biệt tồn tại trong tổng thể các bức tranh nhận được trong phòng trưng bày nghệ thuật không? Chúng ta đặt vấn đề bằng cách giả định rằng giả thuyết không (null hypothesis) rằng giá trị trung bình là giống nhau giữa hai tập hợp mẫu và tiến hành kiểm định t để kiểm tra xem giả thuyết có hợp lý không.
Vì số lượng bản ghi dữ liệu khác nhau (n1 = 10 và n2 = 20) và phương sai cũng khác nhau, giá trị t và độ tự do được tính cho tập dữ liệu trên bằng cách sử dụng công thức được đề cập trong phần Kiểm định T với Phương sai không bằng nhau.
Giá trị t là -2.24787. Vì dấu trừ có thể được bỏ qua khi so sánh hai giá trị t này, giá trị tính toán là 2.24787.
Giá trị độ tự do là 24.38 và được giảm xuống còn 24, do định nghĩa công thức yêu cầu làm tròn giá trị xuống giá trị số nguyên nhỏ nhất có thể.
Một người có thể chỉ định một mức xác suất (mức alpha, mức ý nghĩa, p) là tiêu chí để chấp nhận. Trong hầu hết các trường hợp, có thể giả định một giá trị 5%.
Sử dụng giá trị độ tự do là 24 và mức ý nghĩa 5%, việc xem bảng phân phối giá trị t đưa ra một giá trị là 2.064. So sánh giá trị này với giá trị tính toán là 2.247 cho thấy giá trị t tính toán lớn hơn giá trị trên bảng tại mức ý nghĩa 5%. Do đó, có thể từ chối giả thuyết không (null hypothesis) rằng không có sự khác biệt giữa các giá trị trung bình. Quần thể có những sự khác biệt bẩm sinh, và chúng không phải là do may mắn.
Cách Sử dụng Bảng Phân phối t là như thế nào?
Bảng Phân phối t có sẵn dưới dạng một đuôi và hai đuôi. Đuôi đầu tiên được sử dụng để đánh giá các trường hợp có một giá trị hoặc khoảng có hướng rõ ràng, dương hoặc âm. Ví dụ, xác suất của giá trị đầu ra vẫn dưới -3 là bao nhiêu, hoặc có bao nhiêu khả năng nhận được nhiều hơn bảy khi tung một cặp xúc xắc? Đuôi thứ hai được sử dụng cho phân tích phạm vi, như việc hỏi liệu tọa độ có nằm giữa -2 và +2 không.
T-Test Độc Lập Là Gì?
Các mẫu kiểm định t độc lập được lựa chọn độc lập với nhau, trong đó các tập dữ liệu trong hai nhóm không đề cập đến các giá trị giống nhau. Chúng có thể bao gồm một nhóm 100 bệnh nhân không liên quan ngẫu nhiên được chia thành hai nhóm gồm 50 bệnh nhân mỗi nhóm. Một trong những nhóm trở thành nhóm kiểm soát và được sử dụng điều trị giả dược, trong khi nhóm còn lại nhận một liệu pháp được kê đơn. Điều này tạo thành hai nhóm mẫu độc lập không liên quan đến nhau.
Kiểm Định T Giải Thích và Sử Dụng Như Thế Nào?
Một kiểm định t là một kiểm định thống kê được sử dụng để so sánh các giá trị trung bình của hai nhóm. Thường được sử dụng trong kiểm định giả thuyết để xác định liệu một quy trình hoặc liệu pháp có tác động đến quần thể quan tâm hay không, hoặc liệu hai nhóm có khác biệt với nhau không.
