Buzz
Trong hình học, lăng trụ hình tam giác là một khối đa diện với ba mặt bên. Nó được hình thành từ một đáy hình tam giác, một hình được tạo ra bằng cách tịnh tiến đáy và ba mặt bên nối với các cạnh tương ứng. Lăng trụ tam giác vuông có các mặt bên là hình chữ nhật, trong khi nếu không phải vậy, nó là lăng trụ tam giác xiên. Lăng trụ tam giác đều là một dạng của lăng trụ tam giác vuông với đáy bằng nhau và các mặt bên là hình vuông.
Hơn nữa, đây là một khối đa diện với hai mặt song song, trong khi các mặt còn lại là hình bình hành và nằm trong cùng một mặt phẳng (không nhất thiết phải song song với các mặt phẳng đáy). Các mặt cắt song song với các mặt đáy đều là các hình tam giác giống nhau.
Là một khối đa diện có hình dáng bán nguyệt (hoặc đều)
Hình lăng trụ tam giác vuông có thể được coi là một đa diện đều nếu các mặt cơ bản là tam giác đều và ba mặt bên là hình vuông. Đây là một hình hosohedron tam giác cụt, biểu thị bằng ký hiệu Schläfli
Nhóm đối xứng của lăng trụ tam giác vuông góc có đáy hình tam giác là D3h, bậc 12. Nhóm xoay của nó là D3, bậc 6. Nhóm đối xứng không bao gồm đối xứng tâm.
Thể tích
Thể tích của bất kỳ lăng trụ nào được tính bằng diện tích đáy nhân với chiều cao. Trong trường hợp này, đáy là hình tam giác, vì vậy chỉ cần tính diện tích của tam giác và nhân với chiều dài của lăng trụ:
Trong đó b đại diện cho độ dài của một cạnh của tam giác, h là độ dài của đường cao từ cạnh đó và l là khoảng cách giữa các mặt của tam giác.
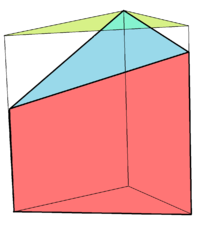
Lăng trụ tam giác cụt
Lăng trụ tam giác cụt vuông có một mặt là hình tam giác cụt được cắt theo góc nghiêng.
Liên kết bên ngoài
- Weisstein, Eric W. 'Lăng kính tam giác'. Từ điển toán học thế giới.
- Khối đa diện tương tác: Lăng kính tam giác
- Diện tích bề mặt và thể tích của hình lăng trụ tam giác Lưu trữ vào ngày 25 tháng 5 năm 2022 tại Wayback Machine
