
Bây giờ rằng Spider-Man: Homecoming đã có sẵn trên đĩa DVD và kỹ thuật số, tôi có thể bắt đầu phân tích vật lý trong những phần yêu thích nhất của bộ phim. Thông thường, tôi thích nghiên cứu về vật lý của siêu anh hùng - việc bay lượn, đi dây, và đánh nhau. Nhưng lần này, vật lý xuất hiện theo một cách khác.
Gần đầu phim, có một cảnh cho thấy Peter Parker trong lớp vật lý của mình. Giáo viên đặt câu hỏi mà trước tiên được Flash trả lời, sau đó là Peter. Nó diễn ra như sau:
Giáo viên: Được rồi, vậy. Làm thế nào để tính gia tốc tuyến tính giữa điểm A và B?
Flash: Tích của sin góc và trọng lực chia cho khối lượng.
Giáo viên: Không đúng. Peter?
Peter: Ummm ... khối lượng bị loại bỏ nên chỉ còn trọng lực nhân với sin.
Cũng có một cái nhìn nhanh vào bảng - mà tôi cho là đi kèm với câu hỏi mà giáo viên đặt ra. Tôi tái tạo lại các phần cơ bản của bản vẽ để bạn có thể thấy họ đang nói gì.
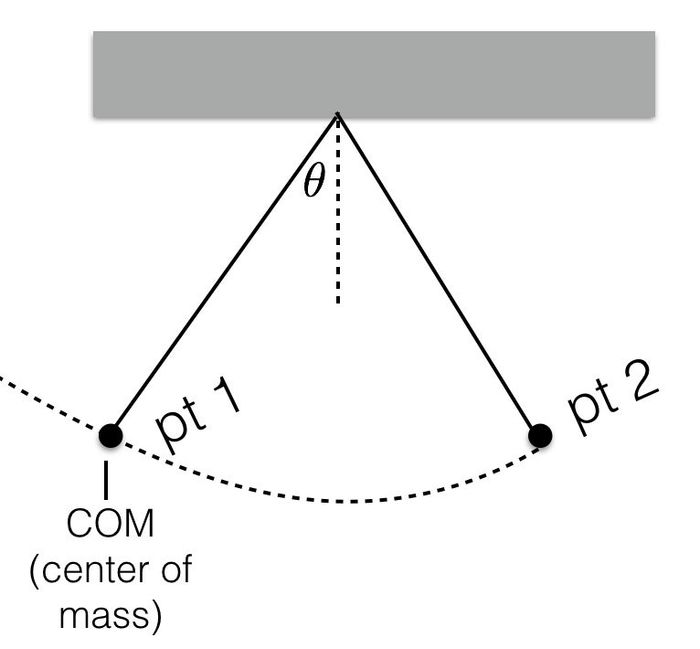
Hóa ra, siêu anh hùng không chỉ minh họa vật lý - họ cũng thực hiện vật lý! Nhưng giống như những bộ phim có thể thể hiện những pha vật lý không hợp lý, chúng cũng có thể làm hỏng ví dụ trên bảng như thế này. Spider-Man: Homecoming đã làm thế nào?
Câu hỏi thực sự đang hỏi gì?
Điều này khó khăn. Phim không thường chứa đựng các thuật ngữ vật lý, nên tôi không chắc chắn 100% về câu hỏi mà giáo viên đang hỏi. "Gia tốc tuyến tính" có nghĩa gì? Thực ra, chỉ có hai lựa chọn. Tuyến tính có thể có nghĩa là ở một chiều. Nhưng vì vấn đề này có thể liên quan đến con lắc treo từ bảng, một chiều không có nhiều ý nghĩa. Lựa chọn khác là tuyến tính có thể có nghĩa là thành phần của gia tốc theo hướng chuyển động. Tôi biết điều này nghe có vẻ kỳ lạ, nhưng hãy để tôi bắt đầu với định nghĩa về gia tốc trung bình:
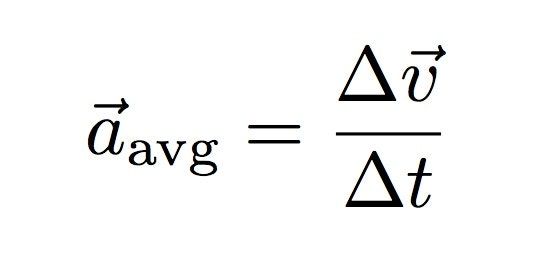
Điều này nói rằng gia tốc là sự thay đổi về vận tốc chia cho một khoảng thời gian nào đó. Nhưng chờ đã! Cả vận tốc và gia tốc đều là vectơ. Bây giờ hãy xem xét về khối lượng này đang dao động trên dây. Khi khối khởi đầu từ một đầu của chuyển động, nó làm hai việc. Đầu tiên, nó tăng tốc độ vì nó đang đi xuống. Thứ hai, nó thay đổi hướng vì dây làm nó di chuyển thành một vòng tròn. Cả hai đều là gia tốc vì bất kỳ thay đổi nào trong vectơ vận tốc (độ lớn hoặc hướng) đều là gia tốc. Vậy nên, gia tốc tuyến tính có thể chỉ là thành phần của gia tốc gây ra sự thay đổi về tốc độ (như thể nó đang di chuyển trong một chiều). Thành phần gia tốc còn lại chỉ gây ra sự thay đổi hướng - điều này được gọi là gia tốc trung tâm.
Được rồi, có một phần khác của câu hỏi của giáo viên làm mơ hồ. "Giữa điểm A và B" có nghĩa là gì? Bản đồ chỉ ra điểm 1 và điểm 2, vì vậy tôi đoán cô ấy nghĩ đến hai điểm đó. Vì vậy, đây là vấn đề thực sự với vấn đề này: Gia tốc không cố định trong giai đoạn đó của con lắc. Điều này làm cho việc tính toán trở nên khá khó khăn (nhưng tôi vẫn sẽ làm). Một lựa chọn khác là tính toán gia tốc chỉ tại một trong các điểm - có thể là điểm 1 hoặc có thể là điểm 2. Hoặc có lẽ cô ấy muốn nói về gia tốc ngay giữa điểm 1 và 2, ngay ở giữa của con lắc. Ai biết được! Tôi không biết Peter đã trả lời câu hỏi này như thế nào.
Câu trả lời thực sự là gì?
Vì tôi thực sự không hiểu câu hỏi, tôi sẽ trả lời tất cả các câu hỏi - và có lẽ cách đó chúng ta có thể hiểu được giáo viên muốn nói gì. Đầu tiên, gia tốc tại điểm 1 (và 2 cũng sẽ cho cùng một câu trả lời)? Hãy để tôi bắt đầu với sơ đồ lực tại điểm 1.
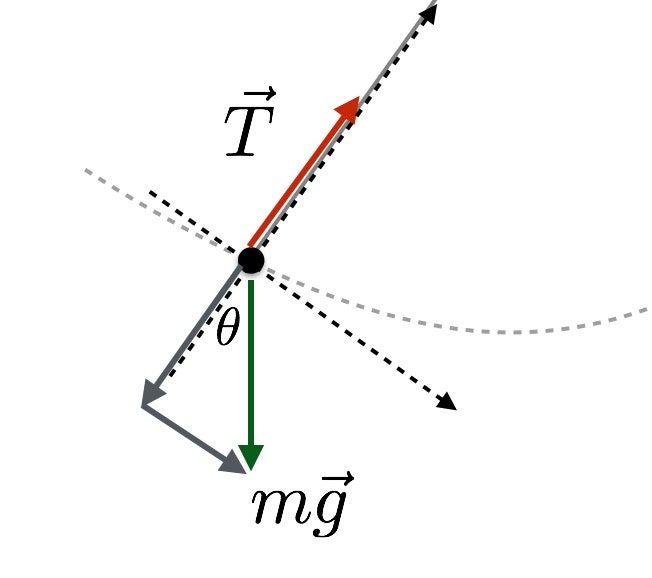
Dây cản trở khối lượng không rời xa hơn từ điểm gối (giả sử dây không bị căng) để giữ cho nó di chuyển trong một đường tròn. Tại điểm 1, khối lượng đứng yên và không gia tốc về phía điểm gối hoặc xa điểm gối. Nó chỉ có thể gia tốc theo hướng vuông góc với dây. Sự căng của dây không kéo ở hướng vuông góc này. Điều đó chỉ để lại một thành phần của lực hấp dẫn với độ lớn:
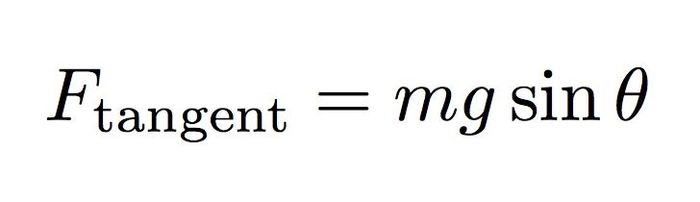
Lực net này bằng tích của khối lượng và gia tốc sao cho gia tốc sẽ là:
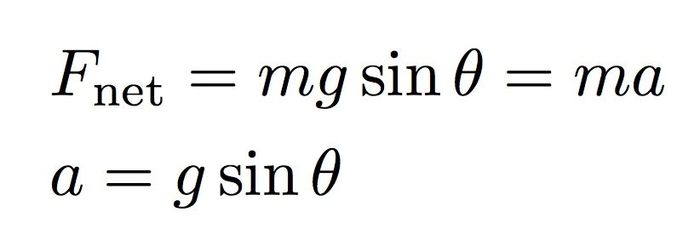
Boom. Đó là câu trả lời mà Peter Parker đã đưa ra. Double boom - đúng vậy, khối lượng thực sự bị loại bỏ. Ngoài ra, đây sẽ là "gia tốc tuyến tính" tại điểm 2 nhưng chỉ theo hướng ngược lại.
Còn về gia tốc trung bình giữa điểm 1 và 2? Điều đó có thể là một phiên bản khác của câu hỏi. Hãy xem xét định nghĩa của gia tốc trung bình từ trên. Gia tốc trung bình là sự thay đổi về vận tốc chia cho sự thay đổi về thời gian. Nếu quả bóng treo bắt đầu và kết thúc ở yên tĩnh, thì cả hai vận tốc này đều bằng không. Sự thay đổi vận tốc này bằng không có nghĩa là gia tốc trung bình cũng là không m/s2. Thực ra, sẽ thú vị nếu Peter trả lời câu hỏi với "khối lượng bị loại bỏ vì gia tốc chỉ đơn giản là không."
Chỉ vui vẻ, đây là một mô hình số của một con lắc dao động. Hãy để tôi cảnh báo bạn, con lắc không phải là vấn đề vật lý đơn giản. Có lẽ nó không thực sự phù hợp cho vật lý cấp 3. Nhưng đây là một mô hình python của một con lắc. Hãy thoải mái thay đổi mã (chỉ cần nhấp vào bút chì để chỉnh sửa và nút play để chạy nó).
Thực ra, với mô hình đó, bạn có thể tìm ra gia tốc cho bất kỳ câu hỏi nào được đặt.
Câu hỏi tốt hơn sẽ là gì?
Mỗi khi tôi chỉ ra điều gì đó không hoạt động tốt trong một bộ phim, tôi thích đề xuất một lựa chọn khác. Nhưng chờ đã. Có lẽ cảnh này vẫn ổn như cách nó đang diễn ra mặc dù câu hỏi không tốt lắm. Có thể cảnh này cho thấy Peter Parker phải đối mặt với những câu hỏi ngớ ngẩn trong đời thực nhưng anh ấy vẫn xử lý chúng tốt.
Nhưng nếu mục tiêu của cảnh là để cho thấy Peter là một nhà khoa học tài ba (anh ấy đã phát minh ra mạng nhện dựa trên hóa chất, sau tất cả), có lẽ giáo viên có thể đã hỏi điều gì đó như thế này:

"Nếu bạn có một con lắc dao động tương tự nhưng có khối lượng lớn hơn, điều gì sẽ xảy ra với chuyển động?"
Peter có thể trả lời:
"Vì cả lực hấp dẫn và gia tốc đều phụ thuộc vào khối lượng, khối lượng bị loại bỏ."
Điều đó có thể là một câu hỏi tốt hơn. Hoặc chờ đã—đây là một câu hỏi tốt hơn nữa:
"Liệu việc chạy hay đu dây có nhanh hơn cho Spider-Man?"
Ồ đợi đã, tôi đã trả lời câu hỏi đó rồi.
Tôi đoán điều này quay trở lại câu hỏi—việc khoa học không hoàn hảo trong một bộ phim có ổn không? Đối với tôi, tôi nghĩ câu trả lời là "có". Mục tiêu của bộ phim là kể một câu chuyện. Nếu khoa học sai giúp xây dựng cốt truyện đó, thì cứ thế đi. Tất nhiên đôi khi nhà làm phim có thể lựa chọn làm sao cho khoa học đúng và tiến triển cốt truyện của bộ phim—đó là trường hợp tốt nhất, nhưng không phải lúc nào cũng có thể. Đòi hỏi khoa học phải hoàn hảo trong phim cũng giống như đòi hỏi các bài báo khoa học phải luôn có vần điệu. Mặc dù điều đó sẽ thú vị...
