Lỗ sâu

Trong lĩnh vực vật lý, một lỗ sâu (tiếng Anh: wormhole), hay còn gọi là Cầu Einstein-Rosen, là một cấu trúc không gian được giả định có cấu trúc đặc biệt tạo ra một đường tắt trong không gian thời gian. Chúng kết nối hai điểm trong không gian thời gian này với nhau và đôi khi cho phép vật chất di chuyển từ một điểm này sang điểm khác thông qua lỗ này.

Thuật ngữ 'lỗ sâu' được tạo ra khi tưởng tượng rằng vũ trụ có hình dạng như một bề mặt cầu. Để đi từ một điểm tới điểm đối diện trên bề mặt cầu, ta cần phải đi qua một quãng đường bằng nửa chu vi của hình cầu lớn. Tuy nhiên, nếu có một con sâu đục lỗ xuyên qua bề mặt hình cầu này, nối trực tiếp hai điểm, quãng đường cần đi sẽ chỉ bằng đường kính của hình cầu.

Trong không gian thời gian, một lỗ sâu có thể giúp vượt qua những khoảng cách rất lớn, thậm chí đi tới một 'vũ trụ khác'. Có thể lỗ sâu tồn tại kéo dài theo thời gian, đi qua cả quá khứ, cho phép việc đi ngược thời gian bằng cách đi qua lỗ sâu.

Một ví dụ về cơ chế hình thành lỗ sâu được đưa ra cho bên trong các lỗ đen điện và quay (với động lượng góc). Tuy nhiên, hiện chưa có bằng chứng thực nghiệm nào cho thấy sự tồn tại của lỗ sâu, và thực tế, chúng gần như không tồn tại. Ngay cả khi một lỗ sâu có thể hình thành theo cơ chế trên, nó sẽ không ổn định; chỉ cần một tác động nhỏ, như là vật chất đi qua nó, cũng có thể làm cho lỗ sâu sụp đổ. Hơn nữa, ngay cả khi lỗ sâu tồn tại và ổn định, việc con người có thể đi qua chúng cũng vô cùng khó khăn, do bức xạ điện từ từ các nguồn như các ngôi sao, sóng vô tuyến của vũ trụ,... sẽ bị tập trung với năng lượng rất lớn, có thể làm hỏng sự sống.

Hình dạng

Để đơn giản hóa khái niệm về lỗ sâu, ta có thể hình dung không gian như một mặt phẳng 2 chiều. Lúc này, lỗ sâu sẽ xuất hiện như một cái hố trên mặt phẳng đó, tạo ra một ống 3 chiều (mặt phẳng bên trong của ống là một ống hình trụ), sau đó nối lại với một vị trí khác trên mặt phẳng 2 chiều đó bằng một cái hố tương tự như vậy ở điểm vào. Một lỗ sâu thực sự sẽ giống như vậy, nhưng chỉ có chiều không gian. Ví dụ, thay vì một cái hố hình tròn trên mặt phẳng 2D, các điểm vào hoặc ra có thể được hình dung như các cái hố hình cầu trong không gian 3 chiều.

Một cách khác để tưởng tượng về lỗ sâu là lấy một tờ giấy và vẽ hai điểm bất kỳ cách xa nhau trên một mặt của tờ giấy đó. Tờ giấy lúc này đại diện cho mặt phẳng không gian, và hai điểm đó đại diện cho một khoảng cách cần di chuyển, nhưng lý thuyết thì lỗ sâu có thể kết nối hai điểm này bằng cách gấp mặt phẳng (trong trường hợp này là tờ giấy) để làm cho hai điểm này gặp nhau. Nhờ vào điều này, ta có thể dễ dàng di chuyển qua khoảng cách này vì hai điểm này đã gặp nhau.

Định nghĩa

Với một không gian compact trong không gian thời gian, có giới hạn bề mặt thông thường nhưng bên trong không phải là đơn giản liên thông. Việc chuẩn hóa ý tưởng này dựa trên giả thuyết sau, được nhắc đến trong Lỗ hổng Lorentz của Matt Visser.

Miêu tả về các lỗ hổng liên vũ trụ (inter-universe wormholes) khó hơn nhiều. Ta có thể tưởng tượng rằng một vũ trụ 'con' được nối với một vũ trụ 'cha' thông qua một 'điểm rốn'. Điểm rốn có thể coi là miệng của lỗ hổng, nhưng do không gian thời gian là liên tục, điều này không hoàn toàn đúng.

Các dạng lỗ hổng

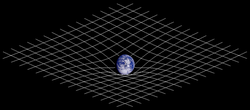
Lỗ hổng liên vũ trụ nối một vị trí này với một vị trí khác trong cùng vũ trụ. Lỗ hổng có thể kết nối các vị trí xa nhau trong vũ trụ bằng cách uốn cong không gian thời gian, cho phép di chuyển giữa chúng nhanh hơn so với di chuyển trong không gian thông thường. Điều này được minh họa bằng hình minh họa. Lỗ hổng liên vũ trụ Một lớp chung của các giải pháp mô tả một hệ thống lỗ hổng đối xứng hình cầu. Sự hiện diện của các hàm tùy ý cho phép mô tả vô số hệ thống lỗ hổng như vậy. Nguồn năng lượng cung cấp cấu trúc bao gồm một sao lùn nâu bị uốn lạ, kết hợp trơn tru với chân không và có thể có hằng số vũ trụ tùy ý. Đã được chứng minh cách tổ hợp các giải pháp này cho phép mật độ năng lượng khác không, do đó giảm thiểu khối lượng sao dương và vi phạm các điều kiện năng lượng. Không giống như các ví dụ đã được xem xét, sự tập trung ở đây là xây dựng bằng cách điều chỉnh trường vật chất ngược với số liệu. Sơ đồ này thường được coi là vật lý hơn phương pháp hình học thuần túy. Cuối cùng, các ví dụ rõ ràng đã được xây dựng bao gồm một ví dụ cho thấy có thể kết nối nhiều vũ trụ đóng với nhau qua các lỗ hổng như vậy. Số lượng vũ trụ được kết nối có thể là hữu hạn hoặc vô hạn. Trong bài báo này, tôi trình bày một không gian thời gian của hai vũ trụ mở được kết nối bởi một lỗ hổng Lorentzian. Không thời gian có những đặc điểm sau: (1) Có thể giải chính xác các phương trình Einstein; (2) Điều kiện năng lượng yếu được đáp ứng tại mọi nơi; (3) Có cấu trúc liên kết R ^ 2 \ lần T_g (g \ ge 2); (4) Không có sự kiện chân không. Điều này đặt ra câu hỏi liệu có loại lỗ hổng nào cho phép di chuyển từ một vũ trụ này sang vũ trụ khác hay không. Một lỗ hổng nối giữa những vũ trụ này được gọi là lỗ hổng Schwarzschild wormhole. Một ứng dụng khác của lỗ hổng là du hành xuyên thời gian, trong đó, hố giun nối một điểm trong không gian thời gian với một điểm khác. Trong lý thuyết dây, lỗ hổng được coi là yếu tố nối hai D-brane với hai miệng nằm trên mỗi brane, được nối với nhau bởi một ống dòng (flux tube). Ngoài ra, lỗ hổng được coi là một phần của bọt thời gian không gian. Có hai loại chính của lỗ hổng: lỗ hổng Lorentz và lỗ hổng Euclid. Lỗ hổng Lorentz được nghiên cứu bởi ngành trọng lực bán cổ điển (semiclassical gravity), trong khi lỗ hổng Euclid được nghiên cứu trong vật lý phân tử. Lỗ hổng khả chuyển (traversible wormholes) là một loại lỗ hổng Lorentz đặc biệt cho phép con người đi từ đầu này đến đầu khác. Sergey Krasnikov đã đề xuất thuật ngữ lối tắt thời gian (spacetime shortcut) là thuật ngữ tổng quát cho lỗ hổng (khả chuyển) và các hệ thống đẩy cho phép di chuyển qua các khoảng cách cực kỳ xa trong thời gian cực kỳ ngắn như động cơ Alcubierre và ống Krasnikov.

Cơ sở lý thuyết

Lỗ sâu có thể bắt qua được

Lỗ sâu và vấn đề di chuyển nhanh hơn tốc độ ánh sáng

Lỗ sâu và vấn đề đi ngược thời gian

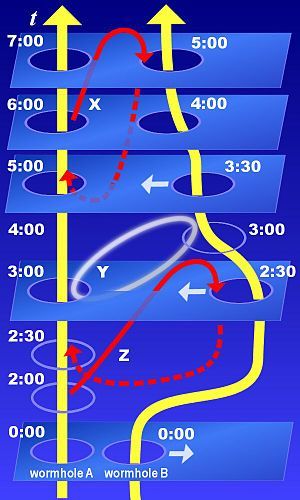
Lỗ sâu Schwarzschild

Lỗ sâu Schwarzschild hoặc cầu nối Einstein-Rosen là những cấu trúc cầu không gian giữa các vùng khác nhau của vũ trụ, được coi là giải pháp không chân không cho các phương trình Einstein khi liên kết hố đen với hố trắng.

Đặc điểm của lỗ sâu

Lỗ sâu là một không gian ba chiều đa tạp có đặc tính địa hình phi thường (tiếng Anh: three-manifold of nontrivial topology)

Lỗ sâu trong văn học, điện ảnh

• Alcubierre drive
• Giả thuyết bảo vệ thời gian
• Nhanh hơn ánh sáng
• Quy tắc tử tinh
• Đường hầm lượng tử
• Đám mây lỗ đen
• Nguyên lý duy trì Novikov
• Vòng Roman
• Sức đẩy từ vũ trụ
• Cổng Stargate SG-1
• Lý thuyết dây
• Lịch sử rộng của thuyết tương đối
• Du hành vượt thời gian

• Visser, Matt. “Vật lý lượng tử của bảo vệ thời gian bởi Matt Visser”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005. Đánh giá rất tốt và ngắn gọn hơn.
• Khatsymosky, Vladimir M. “Hướng tới khả năng tự duy trì của đường hầm giữa các lỗ sâu”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• Roman, Thomas, A. “Một số suy nghĩ về Điều kiện Năng lượng và Cấu trúc lỗ sâu”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
• Krasnikov, Serguei. “Các bất đẳng thức lượng tử không cấm các lối tắt trong thời gian không gian”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• Krasnikov, Serguei. “Ví dụ ngược lại cho một bất đẳng thức lượng tử”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• Teo, Edward. “Các đường hầm xoay vòng có thể đi qua”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• González-Díaz, Pedro F. “Ringholes và các vòng thời gian đóng”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• González-Díaz, Pedro F. “Máy thời gian lượng tử”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• DeBenedictis, Andrew và Das, A. “Về một lớp cấu trúc không gian của các lỗ sâu”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
• Li, Li-Xin. “Hai Vũ trụ Mở Liên Kết Bởi Một Lỗ Sâu: Các Giải Pháp Chính Xác”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• Nandi, Kamal K. và Zhang, Yuan-Zhong. “Một Ràng Buộc Lượng Tử Cho Sự Có Thể Thực Tế Của Lỗ Sâu Lorentzian Cổ Điển”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
• Dzhunushaliev, Vladimir. “Chuỗi trong mô hình vật lý của Einstein”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• Garattini, Remo. “Làm thế nào Foam Spacetime thay đổi tường gạch”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.
• Ori, Amos. “Mô hình máy thời gian mới với lõi hấp thụ nhỏ gọn”. arXiv eprint server. Truy cập ngày 12 tháng 8 năm 2005.

Liên kết ngoài

• Lỗ sâu tại Encyclopædia Britannica (tiếng Anh)
• Đây là thông tin về 'lỗ hổng sao chép' được giải thích bởi Richard F. Holman, William A. Hiscock và Matt Visser.
• Tại sao cần có 'lỗ hổng sao chép'? Lưu trữ 2005-08-28 tại Wayback Machine bởi Matt Visser.
• Lỗ hổng sao chép trong Lý thuyết Tổng quát của Tương đối Lưu trữ 2012-02-22 tại Wayback Machine bởi Soshichi Uchii.
• Thời gian, Du hành Thời gian & Lỗ hổng sao chép có bao gồm một diễn đàn thảo luận.
• Lỗ hổng trắng và Lỗ hổng sao chép Lưu trữ 2011-09-27 tại Wayback Machine cung cấp mô tả rất tốt về lỗ hổng Schwarzschild với đồ họa và hoạt hình, bởi Andrew J. S. Hamilton.
• Câu hỏi thường gặp về Lỗ hổng Đen Lưu trữ 2006-03-16 tại Wayback Machine (Câu hỏi thường gặp) Danh sách bởi Ted Bunn - Câu hỏi thường gặp về lỗ hổng đen