1. Các hoạt động thực hành
Câu hỏi 1:
Thực hiện trò chơi “Ghép thẻ” bằng cách ghép các thẻ tích hợp để có kết quả đúng, ví dụ:
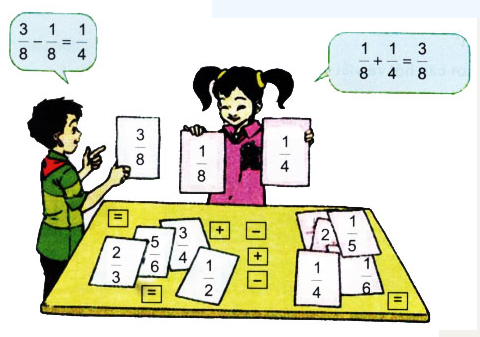
Ghi lại các phép toán nhóm đã ghép thành công.
Nhóm nào ghép đúng nhiều phép toán nhất sẽ là nhóm chiến thắng.
Cách giải:
- Tạo thẻ và chơi trò chơi theo nhóm.
- Sử dụng quy tắc để cộng (hoặc trừ) hai phân số:
+) Để cộng (hoặc trừ) hai phân số có cùng mẫu số, ta chỉ việc cộng (hoặc trừ) các tử số và giữ nguyên mẫu số.
+) Đối với hai phân số khác mẫu số, trước tiên cần quy đồng mẫu số, sau đó thực hiện phép cộng (hoặc trừ).
Giải chi tiết:
Ví dụ minh họa:
1/4 cộng 1/5 bằng 9/20
1/2 cộng 1/6 bằng 2/3
3/4 cộng 1/12 bằng 5/6
9/20 trừ 1/4 bằng 1/5
2/3 trừ 1/2 bằng 1/6
5/6 trừ 3/4 bằng 1/12
9/20 trừ 1/5 bằng 1/4
2/3 trừ 1/6 bằng 1/2
5/6 trừ 1/12 bằng 3/4
Câu hỏi 2:
Tính toán:
a) 10/3 - 8/3; 11/4 - 5/4; 32/17 + 21/17
b) 5/6 + 7/8; 3/7 - 5/14; 7/4 - 3/5
Cách giải:
Áp dụng quy tắc cộng (hoặc trừ) phân số:
- Để cộng (hoặc trừ) hai phân số có cùng mẫu số, chỉ cần cộng (hoặc trừ) hai tử số và giữ nguyên mẫu số.
- Đối với hai phân số khác mẫu số, quy đồng mẫu số rồi thực hiện phép cộng (hoặc trừ). Cách giải chi tiết:
a) 10/3 − 8/3 = (10 - 8)/3 = 2/3
11/4 − 5/4 = (11 - 5)/4;
32/17 + 21/17 = (32 + 21)/17 = 53/17
b) 5/6 + 7/8 = 20/24 + 21/24 = 41/24
3/7 - 5/14 = 6/14 - 5/14 = 1/14
7/4 - 3/5 = 35/20 - 12/20 = 23/20
Câu 3:
Tính:
a) 4 + 1/4;
b) 7/6 − 1;
c) 7 − 8/5;
d) 3/4 + 5
Phương pháp giải:
Chuyển số tự nhiên thành phân số với mẫu số là 1, rồi thực hiện phép cộng (hoặc trừ) hai phân số như bình thường.
Giải chi tiết:
a) 4 + 1/4 = 4/1 + 1/4 = 16/4 + 1/4 = 17/4
b) 7/6 − 1 = 7/6 − 1/1 = 7/6 − 6/6 = 1/6
c) 7 − 8/5 = 7/1 − 8/5 = 35/5 − 8/5 = 27/5
d) 3/4 + 5 = 3/4 + 5/1 = 3/4 + 20/4 = 23/4
Câu 4:
Tìm x:
a) x + 4/5 = 7/5
b) x − 4/3 = 7/4
c) 7/4 − x = 3/14
Phương pháp giải:
Áp dụng các quy tắc sau:
- Để tìm số hạng chưa biết, ta lấy tổng trừ số hạng đã biết.
- Để tìm số bị trừ, ta cộng hiệu với số trừ.
- Để tìm số trừ, ta lấy số bị trừ trừ đi số trừ.
Chi tiết giải quyết:
a) x + 4/5 = 7/5
x = 7/5 − 4/5
x = 3/5
b) x − 4/3 = 7/4
x = 7/4 + 4/3
x = 37/12
c) 4/7 − x = 3/14
x = 4/7 − 3/14
x = 5 / 14
Câu 5: Có một đàn trâu, bò và ngựa đang ăn cỏ. Tỷ lệ trâu là 1/3 của cả đàn, và ngựa chiếm 1/2. Hãy tính tỷ lệ số bò so với tổng đàn? Cách giải:
- Xác định tỷ lệ phần trăm của trâu và ngựa trong tổng đàn.
- Xem toàn bộ đàn như một đơn vị, để tính tỷ lệ số bò, ta lấy 1 trừ đi tỷ lệ của trâu và ngựa trong đàn.
Giải chi tiết: Tổng tỷ lệ của trâu và ngựa là: 1/3 + 1/2 = 5/6 (đàn)
Số bò chiếm tỷ lệ của toàn đàn là: 1 - 5/6 = 1/6 (đàn)
Kết quả: 1/6 đàn.
2. Hoạt động ứng dụng
Câu 1: (trang 51 Toán 4 VNEN Tập 2). Có hai vòi nước cùng chảy vào một bể. Trong cùng thời gian, vòi thứ nhất chảy được 1/4 bể, còn vòi thứ hai chảy được 2/3 bể. Tính lượng nước vòi thứ hai chảy nhiều hơn vòi thứ nhất bao nhiêu phần của bể?
Đáp án: Vòi thứ hai chảy nhiều hơn vòi thứ nhất một lượng bằng:
2/3 - 1/4 = 5/12
Kết quả: 5/12
Câu 2. (trang 51 Toán 4 VNEN Tập 2). Điền phân số thích hợp vào chỗ trống và trình bày cách giải của bạn
Trả lời:

Cách thực hiện: Trước tiên, thực hiện các phép tính theo hàng ngang với các phân số đã cho. Sau đó, tiến hành các phép tính còn lại dựa trên các phân số đã có và phân số mới tìm được.
3. Phương pháp học môn Toán hiệu quả
Để học môn Toán hiệu quả, học sinh cần lưu ý những điểm sau:
- Chú ý lắng nghe bài giảng của giáo viên. Kiến thức trên lớp thường là những phần quan trọng và cần thiết, vì vậy học sinh cần tập trung để hiểu các định lý và công thức toán học quan trọng.
- Để học tốt Toán, cần có đam mê thật sự với môn học. Khi học với niềm hứng thú và yêu thích, học sinh dễ dàng tiếp thu kiến thức hơn. Hãy tạo điều kiện để các em phát triển sự yêu thích với Toán từ sớm, để các em cảm thấy thú vị trong học tập. Đam mê với Toán không khó để nuôi dưỡng, vì chính môn học này có nhiều điều hấp dẫn. Thay đổi cách tiếp cận bài học có thể tạo ra những giờ học thú vị. Tránh áp đặt và kỳ vọng quá cao, vì điều đó có thể gây áp lực cho học sinh. Mặc dù điểm số phản ánh phần nào quá trình học, mục tiêu của việc học Toán là phát triển tư duy và logic. Vì vậy, không nên tạo áp lực quá lớn khi học Toán.
- Để học giỏi môn Toán, học sinh cần kiên nhẫn và luyện tập thường xuyên. Toán học yêu cầu tư duy, nhưng không chỉ dừng lại ở đó, cần phải chăm chỉ làm bài tập và phân tích lời giải thay vì chỉ học thuộc đáp án. Việc hiểu rõ đề bài và ứng dụng kiến thức vào giải bài tập giúp ôn luyện hiệu quả hơn và hiểu sâu hơn về môn học. Môn Toán có thể khó, nhưng học sinh chưa giỏi có thể do chưa có phương pháp học phù hợp. Cần kiên trì và linh hoạt trong việc vận dụng kiến thức để giải quyết các bài toán khó.
- Để học tốt môn Toán, học sinh nên đặt mục tiêu thực tế để cố gắng đạt được. Việc này tạo động lực và giúp duy trì sự kiên trì trong quá trình học tập.
Trên đây là các nội dung liên quan. Để hiểu rõ hơn nội dung, hãy tham khảo: Hướng dẫn giải bài toán bằng cách lập phương trình. Trân trọng.
