Lý thuyết chuyển động

Lý thuyết chuyển động là một lĩnh vực trong cơ học cổ điển nhằm mô tả các chuyển động của điểm, vật thể và hệ thống vật chất mà không xét đến nguyên nhân gây ra các chuyển động đó. Đây là một ngành nghiên cứu, thường được gọi là 'hình học chuyển động' và đôi khi được xem là một phần của toán học. Vấn đề của lý thuyết chuyển động được giải quyết bằng cách mô tả cấu trúc của hệ thống và khai báo các điều kiện ban đầu như vị trí, vận tốc và/hoặc gia tốc của các điểm trong hệ. Sau đó, sử dụng hình học để xác định vị trí, vector và gia tốc của các phần chưa biết trong hệ. Nghiên cứu về tác động của lực lên các đối tượng thuộc về động học, không phải lý thuyết chuyển động. Xem thêm về động học để hiểu rõ hơn.

Lý thuyết chuyển động được ứng dụng trong vật lý thiên văn để miêu tả sự chuyển động của các thiên thể và hệ thống thiên thể, trong kỹ thuật cơ khí, robot học và cơ sinh học để phân tích chuyển động của các hệ thống nhiều bộ phận (hệ thống đa liên kết) như động cơ, cánh tay robot hoặc bộ xương con người.

Các phép biến đổi hình học, còn gọi là phép biến đổi bảo toàn, giúp mô tả chuyển động của các thành phần trong hệ thống cơ khí và đơn giản hóa việc giải các phương trình chuyển động. Chúng cũng đóng vai trò quan trọng trong phân tích động lực học.

Phân tích chuyển động là quá trình đo lường các đại lượng liên quan đến chuyển động để mô tả nó. Trong kỹ thuật, ví dụ, phân tích chuyển động học có thể giúp xác định phạm vi chuyển động của một thiết bị cụ thể và ngược lại, sử dụng tổng hợp động học để thiết kế thiết bị đáp ứng các yêu cầu về quỹ đạo. Thêm vào đó, lý thuyết chuyển động còn sử dụng hình học đại số để nghiên cứu hiệu suất cơ học của hệ thống cơ khí hoặc máy móc.

Định nghĩa thuật ngữ

Thuật ngữ 'kinematic' bắt nguồn từ từ tiếng Anh, được dịch từ cinématique của A.M. Ampère, mà ông đã lấy từ tiếng Hy Lạp cổ đại κίνημα kinema ('sự dịch chuyển, quỹ đạo'), và từ này lại có nguồn gốc từ κινεῖν kinein ('chuyển động').

'Kinematic' và 'cinématique' có liên hệ với từ cinéma trong tiếng Pháp, nhưng không có từ nào trực tiếp bắt nguồn từ nó. Tuy nhiên, cả ba từ đều có nguồn gốc chung, với cinéma là dạng rút gọn của cinématographe, có nghĩa là 'máy chiếu hình ảnh chuyển động và máy ảnh,' từ này cũng được chuyển thể từ tiếng Hy Lạp và được viết bằng chữ cái Hy Lạp.

Chuyển động học của quỹ đạo điểm trong hệ quy chiếu không quay

Chuyển động học của một chất điểm nghiên cứu quỹ đạo của nó. Vị trí của chất điểm được xác định bởi vector tọa độ từ gốc của hệ tọa độ đến chất điểm đó. Ví dụ, nếu có một tòa tháp cao 50 m nằm về phía Nam căn nhà của bạn và gốc tọa độ là nhà bạn, với trục x hướng Đông và trục y hướng Bắc, thì vector tọa độ của đáy tòa tháp là r = (0, −50, 0). Nếu tòa tháp cao 50 m, thì vector tọa độ của đỉnh tháp là r = (0, −50, 50).

Trong trường hợp tổng quát nhất, hệ tọa độ ba chiều được dùng để xác định vị trí của chất điểm. Tuy nhiên, nếu chất điểm chỉ di chuyển trong một mặt phẳng, hệ tọa độ hai chiều là đủ. Tất cả các quan sát vật lý chỉ có giá trị khi được gắn vào hệ tọa độ tham chiếu.

Vector vị trí của chất điểm là một vector kéo từ gốc tọa độ đến chất điểm, thể hiện khoảng cách và hướng từ chất điểm đến gốc tọa độ. Trong hệ tọa độ ba chiều, vị trí của điểm P có thể được biểu diễn dưới dạng

$P=(x_P,y_P,z_P)=x_P\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}+y_P\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}}+z_P\stackrel{^<!--\; ^\; -->}{k},$

với $x_P$, $y_P$ và $z_P$ trong hệ tọa độ Descartes và $\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}$, $\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}}$ và $\stackrel{^<!--\; ^\; -->}{k}$ là các vector đơn vị dọc theo các trục $x$, $y$ và $z$. Độ lớn của vector vị trí $\left|P\right|$ cho biết khoảng cách giữa $P$ và gốc tọa độ.

$|P|=\sqrt{x_P^2+y_P^2+z_P^2}.$

Các cosin chỉ hướng của vector vị trí cho thấy hướng của nó một cách định lượng. Quan trọng là lưu ý rằng vector vị trí của một chất điểm không phải là duy nhất; nó có thể thay đổi tùy thuộc vào hệ tọa độ tham chiếu sử dụng.

Quỹ đạo của một chất điểm là hàm vector theo thời gian, $P\left(t\right)$, mô tả đường cong được vẽ ra bởi chất điểm trong chuyển động, được biểu diễn bởi

$P\left(t\right)=x_P\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}+y_P\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}}+z_P\left(t\right)\stackrel{^<!--\; ^\; -->}{k},$

với tọa độ x_P, y_P và z_P là những hàm thay đổi theo thời gian.

Vận tốc và tốc độ

Vận tốc của một chất điểm là đại lượng vecto thể hiện cả hướng và cường độ của chuyển động. Về mặt toán học, vận tốc là tỉ lệ thay đổi của vector vị trí theo thời gian. Nếu ta chia khoảng cách giữa hai vị trí của chất điểm cho thời gian để di chuyển từ vị trí này đến vị trí kia, ta sẽ có vận tốc trung bình trong khoảng thời gian đó, được định nghĩa bởi công thức: Vận tốc = Độ dời / Thời gian di chuyển

$\stackrel{¯<!--\; ¯\; -->}{V}=\frac{\mathrm{\Delta <!--\; \Delta \; -->}P}{\mathrm{\Delta <!--\; \Delta \; -->}t}$

với ΔP là sự thay đổi của vector vị trí trong khoảng thời gian Δt.

Khi khoảng thời gian Δt trở nên nhỏ vô hạn, vận tốc trung bình trở thành đạo hàm của vector vị trí theo thời gian.

$V=\underset{\mathrm{\Delta <!--\; \Delta \; -->}t\to <!--\; \to \; -->0}{lim}\frac{\mathrm{\Delta <!--\; \Delta \; -->}P}{\mathrm{\Delta <!--\; \Delta \; -->}t}=\frac{dP}{dt}=\stackrel{\dot{}<!--\; \dot{}\; -->}{P}={\stackrel{\dot{}<!--\; \dot{}\; -->}{x}}_{}$

Do vậy, vận tốc chính là tỷ số giữa sự thay đổi của vị trí chất điểm với khoảng thời gian thay đổi, và ký hiệu dấu chấm biểu thị đạo hàm của các hàm x, y và z theo thời gian. Thêm vào đó, vận tốc còn là tiếp tuyến với quỹ đạo của chất điểm tại mọi vị trí trên đường đi của nó. Lưu ý rằng trong hệ quy chiếu không xoay, đạo hàm của các trục tọa độ không được coi là hướng của nó và độ lớn không thay đổi.

Tốc độ của một vật chính là độ lớn |V| của vận tốc. Đây là một đại lượng vô hướng:

$|V|=|\stackrel{\dot{}<!--\; \dot{}\; -->}{P}|=\frac{ds}{dt},$

với s là chiều dài cung được đo theo quỹ đạo di chuyển của chất điểm. Chiều dài cung này thể hiện sự di chuyển của chất điểm theo thời gian và là một đại lượng không giảm. Do đó, ds/dt luôn không âm, nghĩa là vận tốc cũng không âm.

Gia tốc

Vector vận tốc có thể thay đổi cả hướng lẫn độ lớn. Do đó, gia tốc là sự thay đổi tốc độ của vector vận tốc cũng như sự thay đổi hướng của nó. Tương tự như việc xác định vận tốc từ vị trí, gia tốc cũng có thể được xác định từ vector vận tốc. Gia tốc của một chất điểm là vector thể hiện sự thay đổi tốc độ của vector vận tốc. Gia tốc trung bình của chất điểm được tính bằng công thức.

$\stackrel{¯<!--\; ¯\; -->}{A}=\frac{\mathrm{\Delta <!--\; \Delta \; -->}V}{\mathrm{\Delta <!--\; \Delta \; -->}t}$

với ΔV là sự thay đổi của vector vận tốc trong khoảng thời gian Δt.

Gia tốc của chất điểm được xác định là giới hạn của gia tốc trung bình khi khoảng thời gian tiến tới 0, điều này tương đương với việc tính đạo hàm theo thời gian.

Phương trình 1) $A=\underset{\mathrm{\Delta <!--\; \Delta \; -->}t\to <!--\; \to \; -->0}{lim}\frac{\mathrm{\Delta <!--\; \Delta \; -->}V}{\mathrm{\Delta <!--\; \Delta \; -->}t}=\frac{dV}{dt}=\stackrel{\dot{}<!--\; \dot{}\; -->}{V}={\stackrel{\dot{}<!--\; \dot{}\; -->}{v}}_x\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}+{\stackrel{\dot{}<!--\; \dot{}\; -->}{v}}_y\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}}+{\stackrel{\dot{}<!--\; \dot{}\; -->}{v}}_z\stackrel{^<!--\; ^\; -->}{k}$

hoặc

$A=\stackrel{¨<!--\; ¨\; -->}{P}={\stackrel{¨<!--\; ¨\; -->}{x}}_p\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}+{\stackrel{¨<!--\; ¨\; -->}{y}}_P\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}}+{\stackrel{¨<!--\; ¨\; -->}{z}}_P\stackrel{^<!--\; ^\; -->}{k}$

Vì vậy, gia tốc chính là đạo hàm bậc nhất của vector vận tốc và đồng thời là đạo hàm bậc hai của vector vị trí của chất điểm. Cần lưu ý rằng trong hệ quy chiếu không xoay, sự thay đổi của các trục tọa độ không được coi là hướng của nó và độ lớn của nó không thay đổi.

Độ lớn của gia tốc của một vật, ký hiệu là |A|, chính là giá trị vô hướng của vector gia tốc đó.

$|A|=|\stackrel{\dot{}<!--\; \dot{}\; -->}{V}|=\frac{dv}{dt},$

Vector vị trí tương đối

Vector vị trí tương đối là một vector xác định vị trí của một điểm so với một điểm khác, thể hiện sự khác biệt về vị trí giữa hai điểm. Vị trí tương đối của điểm A so với điểm B đơn giản là sự khác biệt giữa các vị trí của chúng.

$P_{A/B}=P_A-<!--\; -\; -->P_B$

đó chính là sự khác biệt giữa các vector vị trí của chúng.

Nếu điểm A có tọa độ thành phần là $P_A=\left(X_A,Y_A,Z_A\right)$

và điểm B có tọa độ thành phần là $P_B=\left(X_B,Y_B,Z_B\right)$

thì vị trí của điểm A so với điểm B sẽ được tính bằng sự khác biệt giữa các tọa độ thành phần của chúng: $P_{A/B}=P_A-<!--\; -\; -->P_B=\left(X_A-<!--\; -\; -->X_B,Y_A-<!--\; -\; -->Y_B,Z_A-<!--\; -\; -->Z_B\right)$

Vận tốc tương đối

Vận tốc của một chất điểm khi so sánh với chất điểm khác có thể đơn giản được hiểu là sự khác biệt giữa các vận tốc của chúng.

$V_{A/B}=V_A-<!--\; -\; -->V_B$

và được tính bằng hiệu giữa các thành phần của vector vận tốc.

Nếu điểm A có các thành phần của vector vận tốc như sau: $V_A=\left(V_{A_x},V_{A_y},V_{A_z}\right)$

và điểm B có các thành phần của vector vận tốc như sau: $V_B=\left(V_{B_x},V_{B_y},V_{B_z}\right)$

thì vận tốc tương đối của điểm A so với điểm B được tính bằng hiệu các thành phần của chúng: $V_{A/B}=V_A-<!--\; -\; -->V_B=\left(V_{A_x}-<!--\; -\; -->V_{B_x},V_{A_y}-<!--\; -\; -->V_{B_y},V_{A_z}-<!--\; -\; -->V_{B_z}\right)$

Ngoài ra, bạn cũng có thể tính vận tốc tương đối bằng cách lấy đạo hàm theo thời gian của vector vị trí tương đối R_B/A.

Khi vận tốc gần bằng tốc độ ánh sáng c (thường là khoảng 95%), ta sử dụng khái niệm tốc độ nhanh, là tỷ lệ giữa V và c, trong thuyết tương đối hẹp.

Gia tốc tương đối

Gia tốc tương đối giữa điểm C và điểm B chính là hiệu gia tốc của chúng

$A_{C/B}=A_C-<!--\; -\; -->A_B$

và được tính bằng cách lấy hiệu của các vecto gia tốc thành phần.

Nếu điểm C có các gia tốc thành phần như sau: $A_C=\left(A_{C_x},A_{C_y},A_{C_z}\right)$

và điểm B có các gia tốc thành phần như sau: $A_B=\left(A_{B_x},A_{B_y},A_{B_z}\right)$

Vậy gia tốc tương đối của điểm C so với điểm B là hiệu giữa các gia tốc thành phần: $A_{C/B}=A_C-<!--\; -\; -->A_B=\left(A_{C_x}-<!--\; -\; -->A_{B_x},A_{C_y}-<!--\; -\; -->A_{B_y},A_{C_z}-<!--\; -\; -->A_{B_z}\right)$

Kết quả tương tự có thể đạt được bằng cách tính đạo hàm bậc hai của vectơ vị trí tương đối P_B/A.

Quỹ đạo của các chất điểm với gia tốc không đổi

Khi gia tốc là một hằng số, phương trình vi phân Eq 1) có thể được tích phân để tìm vector gia tốc 'A' của điểm 'P' với hướng và độ lớn không thay đổi. Một chuyển động như vậy được gọi là chuyển động biến đổi đều. Trong trường hợp này, vận tốc V(t) và quỹ đạo P (t) của chất điểm có thể xác định bằng cách tích phân phương trình gia tốc A theo thời gian.

Giả sử rằng vị trí ban đầu $P_0$, và vận tốc ban đầu $V_0$ tại thời điểm $t=0$ được xác định, tích phân cấp một cho ra vận tốc của chất điểm dưới dạng hàm theo thời gian.

$V\left(t\right)=V_0+{\int <!--\; \int \; -->}_0^{t}Ad\mathrm{\tau <!--\; \tau \; -->}=V_0+At.$

Tích phân cấp hai cho ra quỹ đạo của chất điểm.

$P\left(t\right)=P_0+{\int <!--\; \int \; -->}_0^{t}V\left(\mathrm{\tau <!--\; \tau \; -->}\right)d\mathrm{\tau <!--\; \tau \; -->}=P_0+{\int <!--\; \int \; -->}_0^t(V_0+A\mathrm{\tau <!--\; \tau \; -->})d\mathrm{\tau <!--\; \tau \; -->}=P_0+V_{0}t+\frac{1}{2}A{t}^2.$

Thêm vào đó, mối quan hệ giữa độ dời, vận tốc, gia tốc và thời gian có thể được thiết lập. Do gia tốc là hằng số,

$A=\frac{\mathrm{\Delta <!--\; \Delta \; -->}V}{\mathrm{\Delta <!--\; \Delta \; -->}t}=\frac{V-<!--\; -\; -->V_0}{t}$

$P\left(t\right)=P_0+\left(\frac{V+V_0}{2}\right)t.$

Mối liên hệ giữa vận tốc, vị trí và gia tốc không thay đổi theo thời gian có thể được xây dựng bằng cách sử dụng gia tốc trung bình theo thời gian, và thay thế cùng đơn giản hóa các biểu thức.

$t=\frac{V-<!--\; -\; -->V_0}{A}$

$(P-<!--\; -\; -->P_0)\circ <!--\; \circ \; -->A=\left(V-<!--\; -\; -->V_0\right)\circ <!--\; \circ \; -->\frac{V+V_0}{2}$

dấu ∘ biểu thị tích vô hướng, dùng để chỉ kết quả là một số vô hướng thay vì một vector.

$2(P-<!--\; -\; -->P_0)\circ <!--\; \circ \; -->A=|V{|}^2-<!--\; -\; -->|V_0{|}^2.$

Dấu chấm có thể được thay thế bằng cosin của góc $\mathrm{\alpha <!--\; \alpha \; -->}$ được tạo bởi các vector và tích của chúng, trong trường hợp này:

$2|P-<!--\; -\; -->P_0|\cdot <!--\; \cdot \; -->|A|\cdot <!--\; \cdot \; -->\cos <!--\; \; -->\mathrm{\alpha <!--\; \alpha \; -->}=|V{|}^2-<!--\; -\; -->|V_0{|}^2.$

Khi gia tốc luôn đồng hướng với chuyển động, góc ($\mathrm{\alpha <!--\; \alpha \; -->}$) giữa các vector bằng 0, vì $\cos <!--\; \; -->0=1$, do đó

$|V{|}^2=|V_0{|}^2+2|A|\cdot <!--\; \cdot \; -->|P-<!--\; -\; -->P_0|.$

Có thể đơn giản hóa biểu thức bằng cách dùng ký hiệu độ lớn của vector như sau: $||A||=a,||V||=v,||P-<!--\; -\; -->P_0||=\mathrm{\Delta <!--\; \Delta \; -->}x$ và $\mathrm{\Delta <!--\; \Delta \; -->}x$ có thể là bất kỳ đoạn cong tròn nào trên quỹ đạo, vì vậy

$v^2=v_0^2+2a\cdot <!--\; \cdot \; -->\mathrm{\Delta <!--\; \Delta \; -->}x.$

Như vậy, phương trình tham số chuyển động của vật chuyển thành mối quan hệ giữa tốc độ và vị trí trong hệ tọa độ Descartes, đặc biệt hữu ích khi không biết thời gian. Đồng thời, chúng ta biết rằng $\mathrm{\Delta <!--\; \Delta \; -->}x=\int <!--\; \int \; -->\left(v\right)dt$ hay $\mathrm{\Delta <!--\; \Delta \; -->}x$ là diện tích dưới đường cong a, v, t

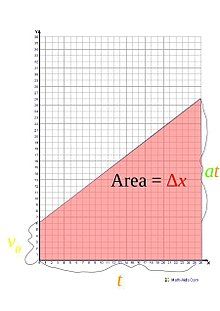
Chúng ta có thể tính $\mathrm{\Delta <!--\; \Delta \; -->}x$ bằng cách cộng diện tích của hình chữ nhật bên dưới với diện tích phần trên của hình tam giác. Diện tích hình chữ nhật là $A\cdot <!--\; \cdot \; -->B$, trong đó $A$ là chiều rộng và $B$ là chiều cao. Ở đây, $A=t$ và $B=v_0$ (với gia tốc khác nhau $a$). Diện tích phần dưới là $t{v}_0$. Diện tích phần trên (hình tam giác) là , với $B$ là cạnh đáy và $H$ là chiều cao. Trong trường hợp này, $B=t$ và $H=at$, nên . Kết quả tổng của $t{v}_0$ và cho kết quả là . Công thức này hữu ích khi vận tốc cuối cùng $v$ chưa được xác định.

Quỹ đạo của chất điểm trong tọa độ cực hình trụ

Để tiện lợi, người ta thường mô tả quỹ đạo của chất điểm P(t) = (X(t), Y(t) và Z(t)) bằng cách sử dụng tọa độ cực trong mặt phẳng X–Y. Điều này giúp biểu diễn vận tốc và gia tốc của chất điểm ở dạng đơn giản hơn.

Nhớ rằng quỹ đạo của chất điểm P được xác định bởi vector tọa độ P đo trong một khung tham chiếu cố định F. Khi chất điểm di chuyển, vector tọa độ P(t) theo quỹ đạo của nó, tạo thành một đường cong trong không gian, được mô tả bởi:

$\text{P}\left(t\right)=X\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}+Y\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}}+Z\left(t\right)\stackrel{^<!--\; ^\; -->}{k},$

Với i, j, và k lần lượt là các vectơ đơn vị dọc theo các trục X, Y, và Z của hệ tọa độ F.

Xem xét một điểm P chỉ di chuyển trên bề mặt của hình trụ với bán kính R(t)=hằng số. Trục Z của hệ tọa độ F có thể được căn chỉnh với trục của hình trụ. Trong trường hợp này, góc θ quanh trục hình trụ trong mặt phẳng X–Y có thể được dùng để mô tả quỹ đạo như sau,

$\text{P}\left(t\right)=R\cos <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}+R\sin <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}}+Z\left(t\right)\stackrel{^<!--\; ^\; -->}{k}.$

Các tọa độ hình trụ của P(t) có thể được đơn giản hóa bằng cách sử dụng các vectơ đơn vị theo hướng xuyên tâm và tiếp tuyến,

${\text{e}}_r=\cos <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}+\sin <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}},{\text{e}}_{\mathrm{\theta <!--\; \theta \; -->}}=-<!--\; -\; -->\sin <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ı<!--\; ı\; -->}}+\cos <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}\left(t\right)\stackrel{^<!--\; ^\; -->}{\mathrm{ȷ<!--\; ȷ\; -->}}.$

và đạo hàm theo thời gian của chúng dựa trên phép tính cơ bản:

$\text{P}\left(t\right)=R{\text{e}}_r+Z\left(t\right)\stackrel{^<!--\; ^\; -->}{k},$

Với quy ước đã chọn, dạng của P(t) sẽ là:

$\text{P}\left(t\right)=R{\text{e}}_r+Z\left(t\right)\stackrel{^<!--\; ^\; -->}{k},$

với R là một hằng số khi điểm chất di chuyển chỉ trên bề mặt của hình trụ có bán kính R.

Nói chung, quỹ đạo của P(t) không nhất thiết phải nằm trên một hình trụ tròn, vì vậy bán kính R có thể thay đổi theo thời gian và quỹ đạo của điểm chất trong hệ tọa độ cực hình trụ sẽ là:

$\text{P}\left(t\right)=R\left(t\right){\text{e}}_r+Z\left(t\right)\stackrel{^<!--\; ^\; -->}{k}.$

Trong đó, các hàm R, theta và Z có thể thay đổi liên tục theo thời gian và ký hiệu hàm đã được rút gọn để đơn giản hóa. Vecto vận tốc V_P là đạo hàm theo thời gian của quỹ đạo P(t), cho ta kết quả:

Tương tự, gia tốc A_P là đạo hàm theo thời gian của vận tốc V_P, được tính như sau:

Thuật ngữ $-<!--\; -\; -->R{\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\theta <!--\; \theta \; -->}}}^2{\text{e}}_r$ biểu thị gia tốc tâm của chuyển động, hay còn gọi là gia tốc hướng tâm. Trong khi đó, thuật ngữ $2\stackrel{\dot{}<!--\; \dot{}\; -->}{R}\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\theta <!--\; \theta \; -->}}{\text{e}}_{\mathrm{\theta <!--\; \theta \; -->}}$ gọi là gia tốc Coriolis.

Bán kính không đổi

Nếu chuyển động của hạt bị giới hạn trên một mặt trụ, thì bán kính R là không đổi và các vectơ vận tốc cũng như gia tốc sẽ trở nên đơn giản hơn. Vận tốc của V_P là đạo hàm theo thời gian của quỹ đạo P(t),

Véc tơ gia tốc trở thành:

Chuyển động theo hình tròn

Một trường hợp đặc biệt của quỹ đạo hạt trên hình trụ tròn là khi không có chuyển động dọc theo trục Z.

$\text{P}\left(t\right)=R{\text{e}}_r+Z_0\stackrel{^<!--\; ^\; -->}{k},$

trong đó R và Z₀ là các hằng số. Trong trường hợp này, vận tốc V_P được tính như sau:

trong đó

$\mathrm{\omega <!--\; \omega \; -->}=\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\theta <!--\; \theta \; -->}},$

là tốc độ góc của vector đơn vị e_θ quanh trục z của hình trụ.

Gia tốc A_P của hạt P hiện tại được tính như sau:

Các thành phần

$a_r=-<!--\; -\; -->R{\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\theta <!--\; \theta \; -->}}}^2,a_{\mathrm{\theta <!--\; \theta \; -->}}=R\stackrel{¨<!--\; ¨\; -->}{\mathrm{\theta <!--\; \theta \; -->}},$

được gọi lần lượt là thành phần radial và tangential của gia tốc.

Kí hiệu cho tốc độ góc và gia tốc góc thường được định nghĩa như sau

$\mathrm{\omega <!--\; \omega \; -->}=\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\theta <!--\; \theta \; -->}},\mathrm{\alpha <!--\; \alpha \; -->}=\stackrel{¨<!--\; ¨\; -->}{\mathrm{\theta <!--\; \theta \; -->}},$

do đó các thành phần gia tốc radial và tangential cho các quỹ đạo tròn cũng được viết là

$a_r=-<!--\; -\; -->R{\mathrm{\omega <!--\; \omega \; -->}}^2,a_{\mathrm{\theta <!--\; \theta \; -->}}=R\mathrm{\alpha <!--\; \alpha \; -->}.$

Chuyển động

Khi một lực tác dụng lên quả bóng, nó sẽ chuyển động từ trạng thái đứng yên đến một vị trí mới. Quá trình này gọi là chuyển động. Do đó, lực làm cho vật thể thay đổi vị trí từ nơi này sang nơi khác, tạo ra hiện tượng chuyển động.

Tính tương đối

Vận tốc của một chuyển động có thể khác nhau tùy thuộc vào từng quan sát viên. Vì vậy, vận tốc là tính tương đối. Ví dụ, một vật có thể di chuyển (có vận tốc khác không) so với một vật khác, nhưng lại đứng yên (vận tốc bằng không) đối với chính nó.

Để đo lường vận tốc, mỗi quan sát viên cần có một hệ trục tọa độ để xác định vị trí trong không gian và một đồng hồ để đo thời gian. Bộ công cụ này gọi là hệ quy chiếu. Các quan sát viên có thể sử dụng các hệ quy chiếu khác nhau và do đó, có thể đo được các vận tốc khác nhau của cùng một vật thể chuyển động. Vì vậy, vận tốc của một chuyển động phụ thuộc vào hệ quy chiếu mà ở đó vị trí và thời gian được ghi lại.

Cộng vận tốc trong Cơ học cổ điển

Như đã đề cập trước đó, vận tốc có tính tương đối và vì vậy có thể có các giá trị khác nhau tùy thuộc vào hệ quy chiếu. Để chuyển đổi vận tốc từ hệ quy chiếu này sang hệ quy chiếu khác, chúng ta dùng phép cộng vận tốc.

Trong Cơ học cổ điển, phép cộng vận tốc được thực hiện bằng cách sử dụng phép cộng véctơ như sau:

Trong đó:

• là vận tốc của A so với B
• là vận tốc của A so với C
• là vận tốc của C so với B

Vì vậy, vận tốc của vật A theo hệ quy chiếu B bằng tổng của vận tốc của A so với hệ quy chiếu trung gian C và vận tốc của hệ quy chiếu C so với hệ quy chiếu B.

Thuyết tương đối hẹp

Trong thuyết tương đối hẹp, khái niệm vận tốc được mở rộng thành vận tốc-4 trong không-thời gian. Nó chính là đạo hàm theo thời gian của véctơ vị trí-4:

với u là véctơ vận tốc trong không gian ba chiều thông thường

và i = 1, 2, 3. Lưu ý rằng:

$U^a{U}_a=-<!--\; -\; -->c^2$

Ghi chú