Lý thuyết hỗn loạn sáng tạo

Thuyết hỗn loạn hay thuyết hỗn mang (chaos theory) là một lĩnh vực nghiên cứu trong toán học và được ứng dụng vào các ngành khoa học khác như vật lý, cơ khí, kinh tế, sinh học, triết học...

Thuyết hỗn loạn nghiên cứu hành vi của các hệ thống động lực (dynamical system) nhạy cảm với điều kiện ban đầu, chúng là những hệ thống phi tuyến tính (non-linear) hoặc có số chiều không gian không giới hạn. Những hệ thống này được đặc trưng bởi tính chất 'hỗn loạn' và sự nhạy cảm của các hệ thống đó thường được nhắc đến như là hiệu ứng cánh bướm (butterfly effect) - một hiện tượng được tìm ra bởi Edward Lorenz. Với đặc tính này, những biến đổi quan sát được của các hệ thống vật lý có biểu hiện hỗn loạn trông có vẻ ngẫu nhiên, dù mô hình mô tả của hệ thống là 'xác định' theo nghĩa là được định nghĩa chính xác và không chứa những tham số ngẫu nhiên. Những biến đổi này có thể được dự đoán trước bằng những phương trình tất định đơn giản (simple deterministic equation).

Về mặt ngữ nghĩa, từ 'hỗn loạn' (chaos từ tiếng Hy Lập χάους) trong ngữ cảnh khoa học mang nghĩa khác với thông thường được sử dụng là trạng thái lộn xộn, thiếu trật tự. Từ hỗn loạn trong thuyết hỗn loạn ám chỉ một hệ thống có vẻ như không có trật tự nào hết nhưng lại tuân theo một quy luật hoặc nguyên tắc nào đó.

Một vài ví dụ của những hệ thống nhạy cảm với điều kiện ban đầu là khí quyển Trái Đất, hệ mặt trời, kiến tạo học, đối lưu chất lỏng, kinh tế, tăng trưởng dân số...

Mô tả về thuyết hỗn loạn

Định nghĩa

Một hệ thống động lực $(T,X,f)$ là hỗn loạn nếu như tồn tại một hàm $f$ bất biến trên tập $Y\subseteq <!--\; \subseteq \; -->X$, nghĩa là $\mathrm{\forall <!--\; \forall \; -->}t\in <!--\; \in \; -->T$ và $\mathrm{\forall <!--\; \forall \; -->}y\in <!--\; \in \; -->Y$, thì $f(t,\mathrm{y\; <div\; class="min-w-[250px]\; max-w-[94vw]\; md:max-w-[770px]">\; <ins\; class="adsbygoogle"\; style="display:block;\; text-align:center;"\; data-ad-layout="in-article"\; data-ad-format="fluid"\; data-ad-client="ca-pub-9247024304160346"\; data-ad-slot="4115752014"></ins>\; </div>})\in <!--\; \in \; -->Y$. Hàm $f$ phải thỏa mãn các tính chất sau:

1. $f$ nhạy cảm với điều kiện ban đầu của $Y$
2. $f$ là hàm chuyển trạng thái topo trên $Y$ thỏa mãn điều kiện:
   Giả sử có các tập mở (open set) $U,V\in <!--\; \in \; -->X$ với $U\cap <!--\; \cap \; -->Y\ne <!--\; \ne \; -->\mathrm{\varnothing <!--\; \varnothing \; -->}\ne <!--\; \ne \; -->V\cap <!--\; \cap \; -->Y$, tồn tại một $t>0$ sao cho $f(t,U)\cap <!--\; \cap \; -->V\ne <!--\; \ne \; -->\mathrm{\varnothing <!--\; \varnothing \; -->}$.
3. Các quỹ đạo tuần hoàn của $f$ là trù mật trên $Y$

Hoặc bằng cách diễn giải thông thường, ta nói một hệ thống động lực là hỗn loạn nếu nó mang các tính chất sau đây:

• nhạy cảm với điều kiện ban đầu (hay phải đáp ứng được hiệu ứng cánh bướm);
• quỹ đạo chuyển động tuần hoàn của hệ thống phải trù mật (dense);
• hòa lẫn nhau theo nghĩa topo (topologically mixing).

Sự vận động mỏ hỗ

Sự nhạy cảm với các điều kiện ban đầu nghĩa là hai điểm trong một hệ như vậy có thể di chuyển trên những quỹ đạo hoàn toàn khác biệt nhau trong không gian pha của chúng ngay cả nếu như sự khác nhau trong cấu hình ban đầu của chúng là rất nhỏ. Hệ này hành xử hoàn toàn giống nhau nếu như cấu hình ban đầu của chúng là giống nhau một cách chính xác. Một ví dụ về độ nhạy cảm như vậy là hiện tượng gọi là 'hiệu ứng bướm', khi mà vẫy cánh của một con bướm được tưởng tượng là tạo ra những thay đổi nhỏ trong khí quyển mà sau một quãng thời gian đủ lớn sẽ tạo nên những thay đổi lớn như là một cơn bão có thể xảy ra. Cái vẫy cánh của con bướm biểu diễn một thay đổi nhỏ trong trạng thái ban đầu của hệ tạo ra một chuỗi các sự kiện để dẫn đến những hiện tượng ở phạm vi rộng lớn hơn như là một cơn bão. Nếu như một con bướm đã không vẫy cánh, quỹ đạo của hệ có thể rất khác xa. Các ví dụ phổ biến khác của các chuyển động hỗn loạn là sự pha trộn của thuốc nhuộm và các dòng khí chuyển động hỗn loạn.

Sự nhạy cảm đối với điều kiện ban đầu liên quan đến hàm mũ Lyapunov.

Hỗn loạn topo

Hỗn loạn topo (topological mixing) hay chuyển động trạng thái topo (topological transitivity) là khi ta áp dụng phép biến đổi lên bất kỳ một đoạn nào $I_1$ sẽ làm nó mở rộng ra cho đến khi chồng lên với một đoạn bất kỳ đã cho trước $I_2$.

Tính hỗn loạn topo, các điểm tuần hoàn trù mật, và sự nhạy cảm đối với điều kiện ban đầu có thể mở rộng ra đến bất kỳ không gian metric nào.

Vùng hấp dẫn

Một cách để nhìn nhận các chuyển động hỗn loạn, hoặc bất kỳ chuyển động nào, là vẽ sơ đồ pha của chúng. Trong sơ đồ này, thời gian không được biểu diễn và mỗi trục đại diện cho một chiều của trạng thái. Ví dụ, ta có thể vẽ vị trí của một con lắc so với vận tốc của nó. Con lắc khi ở vị trí dừng sẽ được biểu diễn bằng một điểm và khi lắc di chuyển tuần hoàn sẽ tạo thành một đường cong khép kín. Khi sơ đồ pha tạo thành một đường cong khép kín, đường cong đó được gọi là một quỹ đạo. Con lắc có vô số quỹ đạo, tạo thành một chuỗi hình elip lồng vào nhau xung quanh gốc tọa độ.

Thường thì sơ đồ pha sẽ cho thấy rằng hầu hết các quỹ đạo trạng thái sẽ quấn quanh và tiến gần tới một ranh giới chung nào đó. Cuối cùng, hệ thống sẽ có một chuyển động giống nhau cho tất cả các trạng thái ban đầu trong một vùng xung quanh chuyển động, như là hệ thống bị hút vào đó. Một chuyển động thu hút như vậy được gọi là một vùng thu hút của hệ thống và là phổ biến cho các hệ thống có sự tiêu tán dần.

Phạm vi của các sự hấp dẫn

Lịch sử

Lý thuyết toán học

Các nhà toán học đã phát hiện nhiều phương pháp mở rộng để đưa ra các đánh giá số lượng về lý thuyết hỗn loạn, trong đó bao gồm:

• Kích thước fractal của điểm thu hút
• Số mũ Lyapunov
• Biểu đồ lặp lại
• Bản đồ Poincaré
• Sơ đồ phân chia
• Toán tử biến đổi

Minh họa sự phức tạp cực tiểu của một hệ thống hỗn loạn

Nhiều hệ đơn giản có thể tạo ra sự hỗn loạn mà không phụ thuộc vào các phương trình vi phân, ví dụ như bản đồ Logistic, là một phương trình sai phân tuyến tính có liên quan lặp lại, mô tả sự gia tăng dân số theo thời gian

Ngay cả với hệ thống rời rạc như xe tự động, có thể phụ thuộc nhiều vào các điều kiện ban đầu. Stephen Wolfram đã nghiên cứu một xe tự động có tính chất này, ông gọi là 'Quy tắc 30'

Những ví dụ khác về các hệ thống hỗn loạn

• Con lắc kép
• Bản đồ Logistic
• Bản đồ Hénon
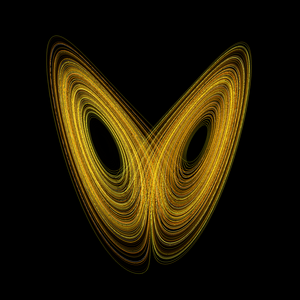
• Mô hình Lorenz
• Giày ngựa Smale
• Bida động lực