- Bài viết này chỉ tập trung vào các khái niệm cơ bản. Để mở rộng hiểu biết, xin tham khảo lý thuyết đồ thị. Đối với ý nghĩa của hàm số trên hệ tọa độ, hãy xem đồ thị hàm số.
Trong lĩnh vực toán học và khoa học máy tính, đồ thị là chủ đề chính của lý thuyết đồ thị. Theo cách hiểu đơn giản, đồ thị là một tập hợp các đỉnh được kết nối bởi các cạnh. Thường thì đồ thị được minh họa dưới dạng các điểm (đỉnh, nút) nối với nhau bằng các đoạn thẳng (cạnh). Tùy vào ứng dụng, một số cạnh có thể có hướng.
Các khái niệm cơ bản
Trong các tài liệu, lý thuyết đồ thị được định nghĩa theo nhiều cách khác nhau. Dưới đây là cách truyền thống theo cuốn từ điển bách khoa này.
Đồ thị không hướng
Đồ thị không hướng hay đồ thị G là một cặp không có thứ tự (unordered pair) G := (V, E), trong đó
- V, tập hợp các đỉnh hoặc nút,
- E, tập hợp các cặp không thứ tự bao gồm các đỉnh khác nhau, được gọi là cạnh. Hai đỉnh trong một cạnh được gọi là các đỉnh đầu cuối của cạnh đó.
Trong nhiều tài liệu, tập hợp các cạnh còn bao gồm cả các cặp đỉnh không phân biệt, những cạnh này được gọi là các khuyên. V (và E) thường là các tập hữu hạn, vì vậy nhiều kết quả nghiên cứu không áp dụng được cho đồ thị vô hạn (infinite graph) do nhiều lý do không phù hợp trong trường hợp vô hạn.
Đồ thị có hướng
Đồ thị có hướng G là một cặp có thứ tự G := (V, A), trong đó
- V, tập hợp các đỉnh hoặc nút,
- A, tập hợp các cặp có thứ tự bao gồm các đỉnh, được gọi là các cạnh có hướng hoặc cung. Một cạnh e = (x, y) có hướng từ x đến y; x là điểm đầu/gốc và y là điểm cuối/ngọn của cạnh.
Đơn đồ thị và Đa đồ thị
Đơn đồ thị là loại đồ thị không chứa khuyên và không có các cạnh song song.
Đa đồ thị là loại đồ thị không đáp ứng tiêu chuẩn của đơn đồ thị.
Đa đồ thị có hướng là một đồ thị có hướng, trong đó nếu x và y là hai đỉnh, thì đồ thị có thể có cả hai cung từ x đến y và từ y đến x.
Đơn đồ thị có hướng (hoặc Đa đồ thị có hướng) là một đồ thị có hướng, trong đó nếu x và y là hai đỉnh, thì đồ thị chỉ có thể chứa tối đa một trong hai cung từ x đến y hoặc từ y đến x.
Quiver thường được coi là một dạng của đồ thị có hướng. Trong thực tế, nó là một đồ thị có hướng với các không gian vector (vector space) gắn liền với các đỉnh và các biến đổi tuyến tính gắn liền với các cung.
Đồ thị hỗn hợp
Đồ thị hỗn hợp G là một bộ ba có thứ tự G := (V, E, A) với V, E và A được định nghĩa như đã nêu.
Các khái niệm khác
Như đã giải thích trước đó, các cạnh của đồ thị vô hướng nối hai đỉnh khác nhau; E và A là các tập hợp (với các phần tử phân biệt). Nhiều ứng dụng yêu cầu các khái niệm mở rộng hơn và các thuật ngữ có thể khác nhau.
Một khuyên (loop) là một cạnh (có hướng hoặc không có hướng) nối từ một đỉnh đến chính nó; việc chấp nhận kiểu cạnh này phụ thuộc vào ứng dụng. Trong ngữ cảnh này, một cạnh nối hai đỉnh khác nhau được gọi là một liên kết (link).
Thỉnh thoảng, E và A có thể là các đa tập hợp (multiset), cho phép nhiều cạnh giữa hai đỉnh. Có thể cho phép nhiều cạnh giữa hai đỉnh bằng cách làm cho E độc lập với V, và xác định điểm đầu của mỗi cạnh bằng một quan hệ liên thuộc (incidence relation) giữa V và E. Đối với đồ thị có hướng, điều này áp dụng tương tự cho tập hợp cạnh có hướng A, nhưng yêu cầu hai quan hệ liên thuộc, một cho đỉnh đầu và một cho đỉnh cuối của mỗi cung.
Trong các tài liệu, tùy theo quan điểm của tác giả hoặc yêu cầu của chủ đề, từ 'đồ thị' có thể bao gồm hoặc không bao gồm khuyên và đa cạnh. Nếu đồ thị không cho phép đa cạnh (và không cho phép khuyên nếu là đồ thị có hướng), nó được gọi là đơn đồ thị. Ngược lại, nếu đồ thị cho phép đa cạnh (và đôi khi cả khuyên), nó được gọi là đa đồ thị. Thuật ngữ giả đồ thị (pseudograph) thường được dùng để chỉ cả hai loại đều được phép. Trong một số trường hợp đặc biệt, còn cần đến các cạnh chỉ có một đỉnh, gọi là nửa cạnh (halfedge), hoặc không có đỉnh nào, gọi là cạnh rời. Xem ví dụ tại signed graph.
Các khái niệm khác
Hai cạnh trong một đồ thị được gọi là kề nhau nếu chúng chia sẻ một đỉnh chung. Tương tự, hai đỉnh được coi là kề nhau nếu chúng được nối bởi một cạnh. Một cạnh và đỉnh nằm trên cạnh đó được xem là liên thuộc với nhau.
Đồ thị có một đỉnh và không có cạnh nào được gọi là đồ thị tầm thường. Đồ thị không có cả đỉnh lẫn cạnh được gọi là đồ thị rỗng.
Trong một đồ thị có trọng số, mỗi cạnh được gán một giá trị gọi là trọng số, độ dài, chi phí, hoặc các tên khác tùy thuộc vào ứng dụng; các đồ thị này thường được sử dụng trong các bài toán tối ưu hóa đường đi như bài toán người bán hàng.
Ví dụ
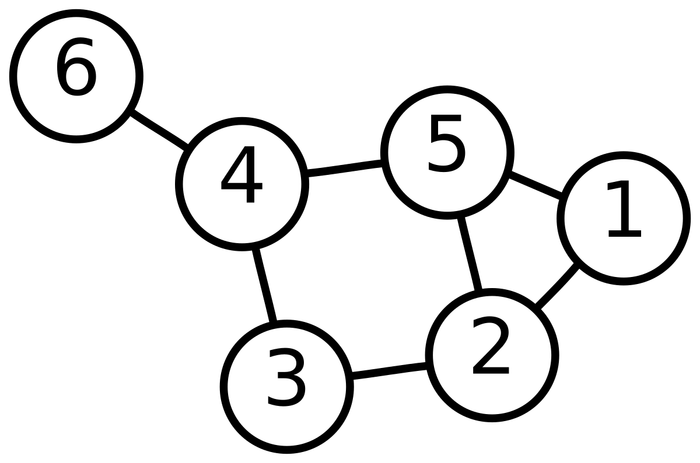
Hình dưới đây minh họa đồ thị được mô tả sau đây
- V := {1, 2, 3, 4, 5, 6}
- E := Bản mẫu: {1, 2}, {1, 5}, {2, 3}, {2, 5}, {3, 4}, {4, 5}, Bản mẫu: {4, 6}
Thỉnh thoảng, thông tin 'đỉnh 1 nối với đỉnh 2' được ký hiệu là 1 ~ 2.
- Trong lý thuyết phạm trù (category theory), một phạm trù có thể coi là một đa đồ thị có hướng với các đối tượng là các đỉnh và các morphism là các cạnh có hướng. Khi đó, các hàm tử (functor) giữa các phạm trù là một số (nhưng không nhất thiết tất cả) các morphism của đồ thị có hướng.
- Trong khoa học máy tính, đồ thị có hướng được sử dụng để mô tả các ô-tô-mát hữu hạn (finite state machine) và nhiều cấu trúc rời rạc khác.
- Một quan hệ đôi (binary relation) R trên tập X là một đồ thị có hướng đơn. Hai đỉnh x, y trong X được nối với nhau bằng một cung nếu xRy.
Các loại đồ thị quan trọng
- Trong một đồ thị đầy đủ, mỗi cặp đỉnh đều được nối với nhau bằng một cạnh, tức là đồ thị bao gồm tất cả các cạnh có thể có.
- Một đồ thị phẳng có thể được vẽ trên mặt phẳng mà không có hai cạnh nào cắt nhau.
- Cây là một đồ thị liên thông không chứa chu trình nào.
- Đồ thị hai phía (Bipartite graph)
- Đồ thị hoàn hảo (Perfect graph)
- Cograph
- Đồ thị Cayley
- Đồ thị Petersen và các mở rộng của nó
Các phép toán trên đồ thị
Có nhiều phép toán để tạo ra các đồ thị mới từ các đồ thị đã cho.
Các phép toán đơn
- Đồ thị đường (Line graph) (tạo ra đồ thị mới bằng cách chuyển đổi các cạnh thành đỉnh và tạo các cạnh nối giữa các đỉnh mới tương ứng với các cạnh ban đầu)
- Đồ thị đối ngẫu (Dual graph) (tạo ra đồ thị mới từ một đồ thị phẳng bằng cách gán một đỉnh cho mỗi miền mặt phẳng và nối các đỉnh tương ứng với các miền kề nhau)
- Đồ thị bù (Complement graph)
Các phép toán hai đối tượng
- Tích Đề-các của đồ thị (Cartesian product of graphs)
- Tích Ten-xơ của đồ thị (Tensor product of graphs)
Các mở rộng
Trong siêu đồ thị (hypergraph), một cạnh có thể kết nối nhiều hơn hai đỉnh.
Một đồ thị vô hướng có thể được xem như một phức hợp đơn hình (simplicial complex) bao gồm các đơn hình 1 chiều (các cạnh) và các đơn hình 0 chiều (các đỉnh). Do đó, đa hình là một mở rộng của đồ thị, vì chúng cho phép các đơn hình có nhiều chiều hơn.
Mỗi đồ thị tương ứng với một matroid, nhưng thường không thể khôi phục lại đồ thị từ matroid của nó, do đó, matroid không phải là một mở rộng của đồ thị.
Trong lý thuyết mô hình (model theory), một đồ thị được coi là một cấu trúc. Không có giới hạn về số lượng cạnh: nó có thể có số lượng bất kỳ.
- Đa giác
- Bài toán lát gạch (Tiling)
- Các thuật ngữ trong lý thuyết đồ thị
- Danh sách các chủ đề trong lý thuyết đồ thị
- Đồ thị (cấu trúc dữ liệu)
- Các ấn phẩm quan trọng về lý thuyết đồ thị
