1. Khái niệm động lượng
Động lượng là đại lượng vật lý phản ánh khả năng truyền chuyển động của một vật. Đối với một vật có khối lượng m đang di chuyển với vận tốc v, động lượng p được tính bằng công thức p = m.v. Định luật bảo toàn động lượng cho biết tổng động lượng của hệ thống không thay đổi nếu không có lực bên ngoài tác động.
+ Công thức:
Δp = p1 − p1′ = m1(v1 ′ − v1): Diễn tả sự thay đổi động lượng p của vật có khối lượng m, với v1 và v1 ′ là vận tốc trước và sau sự kiện.
+ Công thức:
Δp = p1′ + p2′ − (p1 + p2): Mô tả sự thay đổi động lượng của hệ hai vật có khối lượng m1 và m2, trong đó pi và pi′ là động lượng của vật i trước và sau khi xảy ra sự kiện.
+ Công thức:
F.Δt = Δp: Diễn tả xung lượng của lực F trong thời gian Δt, cho thấy sự liên hệ giữa lực và sự biến thiên động lượng của vật.
Trong trò chơi giật khăn, xung lượng của lực được thể hiện qua việc kéo khăn nhẹ và từ từ khiến vật trên bàn rơi xuống, trong khi kéo mạnh và nhanh có thể giữ cho vật không rơi.
2. Định luật bảo toàn động lượng
Định luật bảo toàn động lượng khẳng định rằng tổng động lượng của một hệ kín không thay đổi trong mọi quá trình tương tác như va chạm hay nổ. Điều này có nghĩa là động lượng của các vật trong hệ trước sự kiện sẽ bằng động lượng của các vật sau sự kiện, miễn là hệ đó không chịu tác động từ bên ngoài. Một hệ kín là hệ mà tổng lực tác động vào nó là 0 hoặc không có tương tác với môi trường ngoài.
Ví dụ áp dụng định luật bảo toàn động lượng là khi đạn nổ, nơi năng lượng sinh ra từ vụ nổ rất lớn so với lực bên ngoài, nên có thể coi đây là một hệ kín và áp dụng định luật. Đối với hai vật va chạm, công thức bảo toàn động lượng là m1.v1 + m2.v2 = m1.v1′ + m2.v2′, trong đó m1 và m2 là khối lượng của hai vật, v1 và v2 là vận tốc của chúng trước va chạm, và v1′ cùng v2′ là vận tốc sau va chạm.
Công thức tương tự áp dụng cho trường hợp chuyển động phản lực, khi một vật với vận tốc v tách thành hai vật với vận tốc v1 và v2. Công thức cho trường hợp này là: m⋅v = m1.v1 + m2.v2. Ở đây, m là khối lượng ban đầu của vật, v là vận tốc ban đầu, m1 và m2 là khối lượng của hai vật sau khi tách, và v1 cùng v2 là vận tốc của hai vật sau khi tách.
3. Một số bài tập áp dụng liên quan
Câu 1. Một chiếc xe có khối lượng 1 tấn đang di chuyển với vận tốc 36 km/h thì phanh và dừng lại sau 5 giây. Tính lực phanh (giải bằng hai phương pháp khác nhau theo định luật II Niu-ton).
Hướng dẫn giải:
Chọn đối tượng phân tích là xe, và chọn chiều dương theo hướng chuyển động của xe.
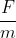
=> Gia tốc: a = -2 (m/s2)
Lực phanh: F = ma = 1000 × (-2) = -2000
b) Phương pháp 2: Áp dụng định luật II Niu-tơn dưới dạng tổng quát:
+ Sự thay đổi động lượng = -10000 (kg.m/s)
+ Lực phanh: F = -2000 N
Do đó: Lực phanh có độ lớn 2000 N và ngược chiều với hướng chuyển động của xe.
Câu 2. Xác định lực mà súng trường tác động lên vai người bắn, biết rằng khi bắn, vai người bắn lùi lại 2cm, và viên đạn thoát khỏi nòng súng với vận tốc 500 m/s. Khối lượng súng là 5kg và khối lượng đạn là 20g.
Hướng dẫn giải:
Chọn hệ nghiên cứu: Súng và đạn.
- Quá trình lùi của súng gồm hai giai đoạn:
+ Giai đoạn 1: Viên đạn đang di chuyển trong nòng súng.
+ Giai đoạn 2: Viên đạn đã rời khỏi nòng súng.
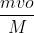
- Xem xét chuyển động của súng sau khi viên đạn đã rời nòng. Giả sử súng giảm tốc đều với vận tốc ban đầu là v và di chuyển quãng đường s = 2cm cho đến khi dừng lại do lực cản F (coi như lực ma sát) từ vai người bắn.
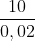
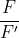
Câu 3. Một tên lửa có khối lượng 500 kg đang di chuyển với vận tốc 200 m/s thì phân tách thành hai phần. Phần bị tách ra có khối lượng 200 kg sau đó di chuyển ra phía sau với vận tốc 100 m/s so với phần còn lại. Tính vận tốc của từng phần.
Hướng dẫn giải:
Chọn hệ nghiên cứu: “Tên lửa”. Trong quá trình phân tách, nội lực của tên lửa lớn so với trọng lực nên hệ có thể coi là kín theo phương ngang.
Gọi m là tổng khối lượng của tên lửa; m1 là khối lượng của phần bị tách ra; v1 là vận tốc của phần tách ra so với Trái Đất; vo là vận tốc của phần tách ra so với phần còn lại; v là vận tốc của tên lửa trước khi phân tách; v2 là vận tốc của phần còn lại sau khi phân tách. Vì các vận tốc cùng phương nên ta có: v1 = vo + v2
- Áp dụng định luật bảo toàn động lượng, ta có: mv = m1v1 = (m - m1)v2
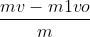
Chọn chiều dương theo hướng chuyển động của tên lửa trước khi tách, ta có: v = 200 m/s; vo = 240 m/s
- Từ công thức (2) suy ra: v2 = 240 m/s
- Từ công thức (1) suy ra: v1 = -100 + 240 = 140 m/s
* Nhận xét:
+ Vì v1 > 0 và v1 < v nên sau khi phân tách, phần tách ra vẫn di chuyển về phía trước nhưng với vận tốc chậm hơn.
+ Vì v2 > 0 và v2 > v nên sau khi phân tách, phần còn lại vẫn di chuyển về phía trước nhưng với vận tốc nhanh hơn, tức là được gia tốc.
Câu 4. Một người có khối lượng m1 = 50 kg đang đứng trên một chiếc thuyền khối lượng m2 = 200 kg nằm yên trên mặt nước tĩnh. Sau đó, người này đi từ mũi đến lái thuyền với vận tốc v1 = 0,5 m/s so với thuyền. Biết thuyền dài 3m, bỏ qua lực cản của nước.
a) Tính vận tốc của thuyền so với dòng nước.
b) Trong khi người di chuyển, thuyền đi được quãng đường bao nhiêu?
c) Khi người dừng lại, thuyền còn tiếp tục chuyển động không?
Hướng dẫn giải:
Chọn hệ phân tích: thuyền và người. Vì không tính đến lực cản của nước, hệ này là hệ kín và lực tác động bên ngoài được cân bằng.
a) Tính vận tốc của thuyền so với dòng nước.
Gọi: + v1 là vận tốc của người so với thuyền.
+ v2 là vận tốc của thuyền so với mặt nước.
+ v3 là vận tốc của người so với mặt nước.
- Theo công thức cộng vận tốc, ta có: v3 = v1 + v2
Chọn chiều dương theo hướng di chuyển của người: v1 > 0
- Áp dụng định luật bảo toàn động lượng cho hệ (xem trong hệ quy chiếu gắn với mặt nước): m1v3 + m2v2 = 0 -> v2 = -0,1 m/s < 0
Vậy: Thuyền di chuyển ngược chiều với người với vận tốc có độ lớn 0,1 m/s.
b)
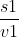
- Quãng đường thuyền di chuyển được: s2 = v2t = 0,6 m
c) Chuyển động của thuyền khi người dừng lại: Khi người dừng lại, vận tốc của người là v1 = 0.