Buzz
Hàm số mũ là gì?
Dựa vào kiến thức cấp 3, hàm số mũ được biểu diễn dưới dạng y= f(x) = ax. Ở đây, a là số thực > 0 và khác 1, được biểu diễn bằng hàm số mũ với cơ số a.
Chú ý: Hàm Logarit là hàm ngược của hàm số mũ.
Nếu theo đạo hàm, hàm số mũ sẽ có công thức phụ thuộc vào 2 định lý dưới đây:
2 nguyên tắc quan trọng về hàm số mũ bạn cần nhớ
Hàm Logarit là gì?
Hàm Logarit là loại hàm số có dạng
được biểu diễn dưới dạng Logarit. Nói một cách đơn giản, Logarit là phép toán đảo ngược của lũy thừa hoặc số lần lặp lại của một phép nhân nào đó.
Trong kiến thức THPT, chúng ta thường gặp hàm số y=log
một sốx, được diễn giải như hàm số Logarit với cơ số a. Ở đây, a là số thực dương lớn hơn 0 và khác 1.
Tính chất của hàm Logarit và hàm số mũ
Tính chất của hàm số mũ
- Hàm số mũ có miền xác định là toàn bộ tập số thực R.
- Đạo hàm của nó là: ∀x∈R, y′=ax ln a.
- Có sự biến đổi theo chiều biến thiên.
Để xác định tính chất đồng biến hay nghịch biến của hàm số, chúng ta cần xem xét giá trị của cơ số a:
- Nếu a nằm trong khoảng từ 0 đến 1 (0<1) thì hàm số mũ sẽ luôn giảm.
- Nếu a lớn hơn 1 (a>1) thì hàm số mũ sẽ luôn tăng.
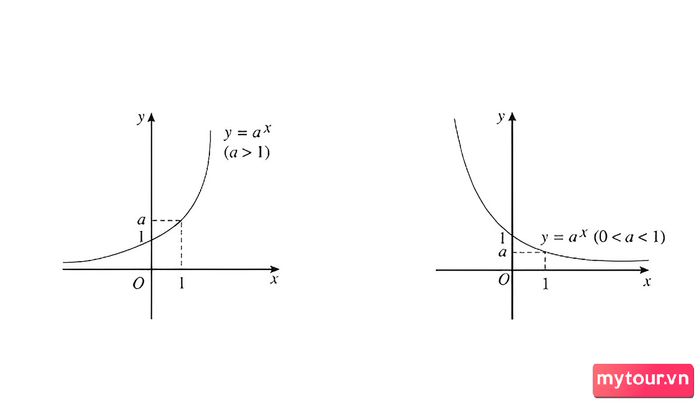Nếu a>1, hàm số mũ là đồng biến, với a=0<
Tính chất của hàm Logarit
Công thức của hàm Logarit là y= log
ax (a khác 1 và lớn hơn 0)
Trong đó:
- TXĐ: (0;+∞)
- Đạo hàm y’=1/x ln a, ∀ x ∈ (0;+∞)
Chiều biến thiên của hàm số như sau:
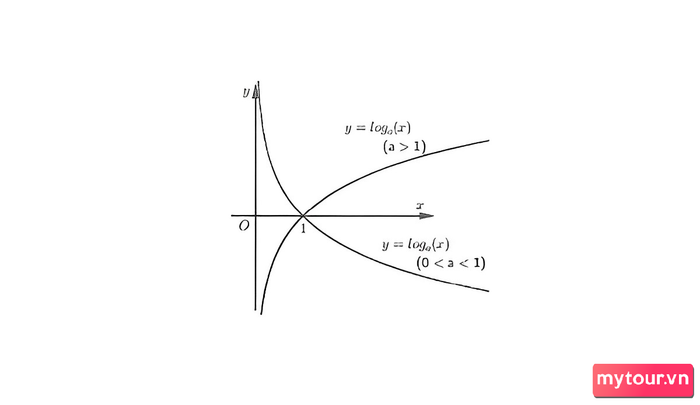Hàm số đồng biến khi a>1, nghịch biến khi 0<1.
Đồ thị hàm số mũ và hàm Logarit
Các bước vẽ đồ thị hàm số mũ
Bước 2: Xác định giới hạn bằng cách tạo bảng biến thiên.
Để hiểu rõ, mời các bạn theo dõi ví dụ sau đây:
Ví dụ: Hãy vẽ đồ thị hàm số y=(3/2)
x
Bài giải cho ví dụ về việc vẽ đồ thị hàm số mũ
Các bước vẽ đồ thị hàm Logarit
Bước 1: Xác định tập xác định từ hàm số đã cho.
Bước 2: Xác định tính đồng biến hoặc nghịch biến của hàm theo công thức.
Bước 3: Vẽ đồ thị.
Để hiểu rõ, mời các bạn theo dõi ví dụ sau đây:
Ví dụ: Hãy vẽ đồ thị của hàm số y = log
5x
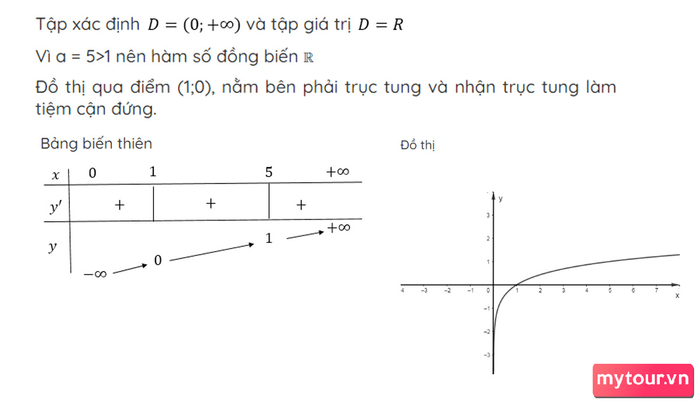Bài giải và phương pháp vẽ đồ thị Logarit
Chú ý khi sử dụng hàm Logarit
Để xác định nhanh tính đồng biến hoặc nghịch biến của hàm số Logarit và hàm số mũ, bạn có thể áp dụng 2 chú ý sau:
- Hàm số Logarit và hàm số mũ có cơ số a > 1 thì luôn luôn đồng biến.
- Ngược lại, Hàm số Logarit và hàm số mũ có cơ số a < 1 thì luôn luôn nghịch biến
Dưới đây là công thức mở rộng của đạo hàm Logarit:
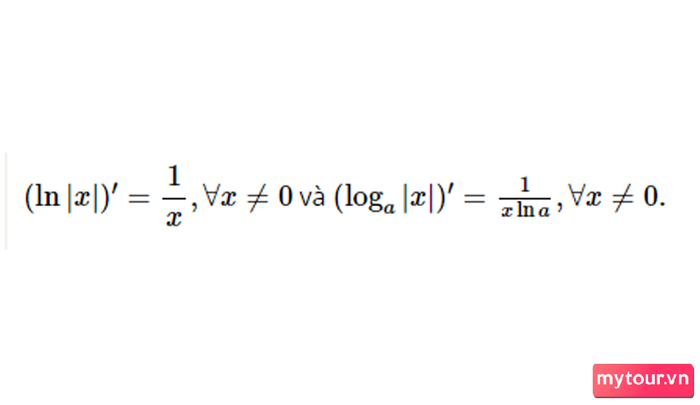
Bài viết này chứa đựng toàn bộ lý thuyết, tính chất, ví dụ và cách vẽ đồ thị về hàm số mũ và hàm Logarit. Hy vọng bạn sẽ áp dụng thành công các công thức này trong các bài toán. Chúc bạn đạt điểm cao trong kỳ thi sắp tới.
